• Math tutors
• /
• Knowledge Base
• /
• Area Model Division – Definition, Examples, Facts

Area Model Division – Definition, Examples, Facts

Welcome to Brighterly, where we take the complexity out of math to give you confidence!

Today, we’re going to explain the area model division, a method for making division easier.

Here, we’ll cover what the division area model is, how it works and its benefits. We’ll also share practice test problems and engaging worksheets so you can continue your learning.

What is area model division?

The area model for division is a method of teaching division that breaks up the equation. It can be used with decimals and whole numbers to divide numbers that aren’t divisible. We cover the full definition of area model division below with examples.

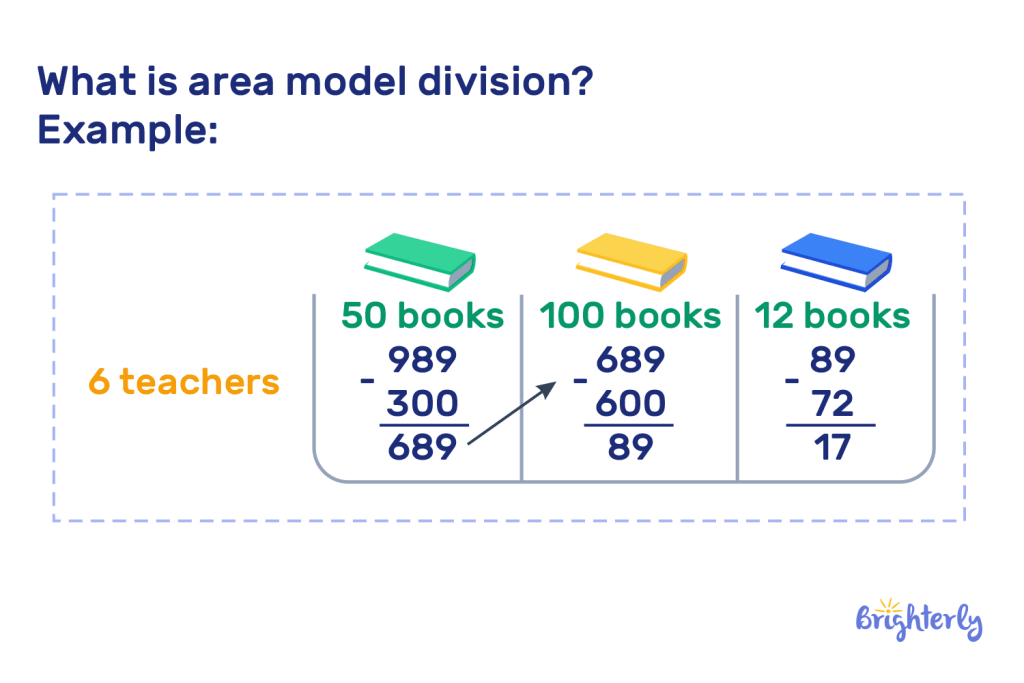
Definition of area model division

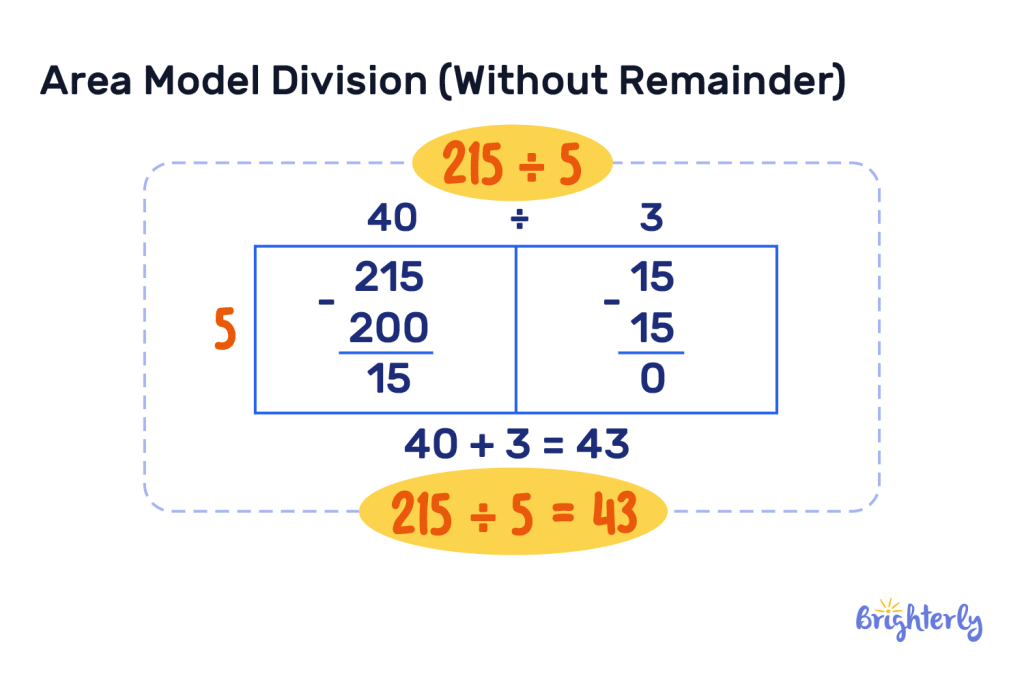
The area model of division definition is a model that can be used for division. It involves both visuals and incorporating multiplication and subtraction. First, you create a rectangle. Let’s use the example of 215 ÷ 5. You’d place 215 inside your box, and 5 on the left of your box.

Rather than trying to solve this large sum in one go, you can use multiplication and subtraction. Think about multiples of 5:

• 1 x 5 = 5
• 5 x 5 = 25
• 10 x 5 = 50

Use these multiples of 5 to subtract from your number of 215 and create additional blocks in your rectangle. So we know 10 x 5 is 50, and we can take that away from 215 4 times, so you multiply them together. This becomes your first block in your rectangle, with 40 at the top.

Now, we have 15 left over to divide. We know we can subtract 5 from 15 3 times and then reach 0. Put 3 at the top of your second block.

Now, you add the numbers at the top of your block to get your answer. 40 + 3 = 43. Therefore, 215 ÷ 5 = 43.

How does area model division work?

Division using the area model breaks up a complex division into smaller, more manageable parts. By taking multiples of your divisor (the number you’re dividing by) away from your dividend (the number you’re dividing), you can break down a complex equation and make it easier to solve. Because we’re taking all of these numbers away from our dividend, we still get the same result no matter what.

Benefits and uses of area model division

The benefits of division with area model are two-fold. Firstly, this model for division helps learners visualize division problems. This is especially useful for kids who are visual learners. 

Secondly, it simplifies large and complex division operations by breaking them down into smaller chunks. Many kids, when learning math operations, find division the most difficult to grasp. Therefore, by multiplying our divisor and taking those multiples away from our dividend, we are making the division easier to solve.

Examples of area model division

Let’s take another example of area model division. We have to divide 943 by 23.

• First, let’s work out some simple multiples of 23. We know 10 x 23 is 230, and that we can take that away from 943 multiple times
• 4 x 230 is 920, so we can subtract this from 943. This means we’ve taken 23 away from 943 40 times, so we put that at the top of our block
• Now, we only have 23 remaining, so we take that away once to get to 0
• Finally, we add the number of times we’ve taken away 23 from 943. 40 + 1 = 41
• Therefore, 943 ÷ 23 = 41.

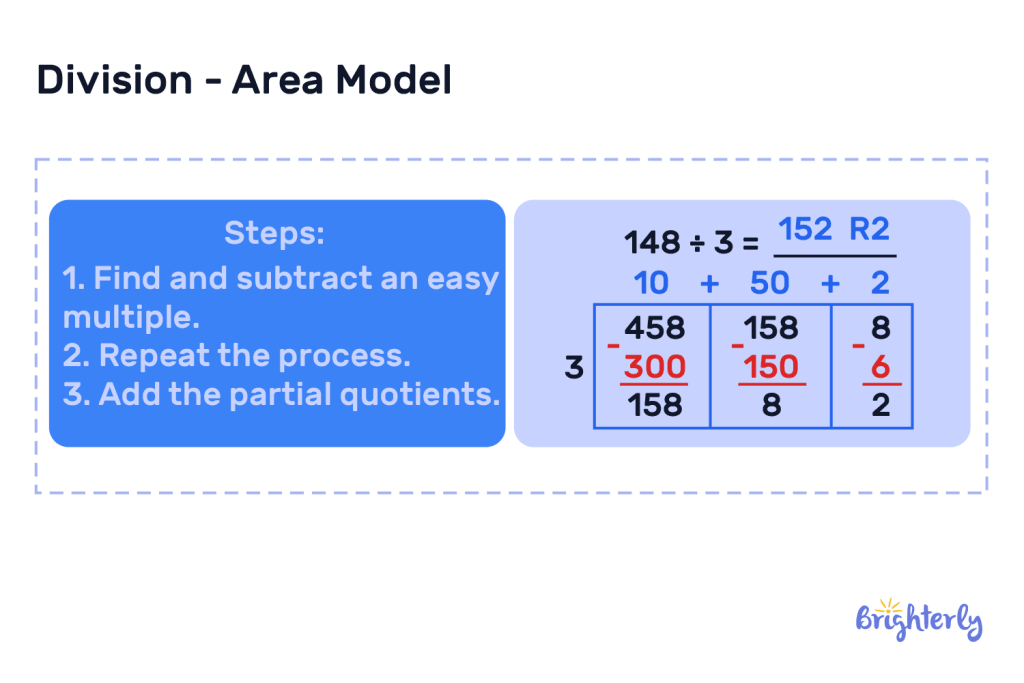
Steps in area model division

There are some simple steps you take to use division with area model:

• Draw a rectangle and write your dividend in the center, then your divisor to the left of the rectangle
• Identify multiples of your divisor that can be taken away from your dividend, and subtract them
• Continue doing this until you’re left with 0
• Count up the number of times you’ve taken away your divisor from your dividend – that’s the answer to your division equation

Properties and characteristics of area model division

There are some properties and characteristics of the area division model that make it both useful and unique:

• It adds a visual element to division, which can be helpful for visual learners
• It simplifies complex division problems, making them easier to solve
• It incorporates multiplication and subtraction, which are often easier for learners to work with
• It encourages kids to think beyond learning by rote

Comparing area model division with other division models

Area model division is different from other models. Many division models can divide faster, like the long division area model, but this model for division focuses on simplifying the calculation and making it easier to do. It’s a great method for younger kids, or kids who aren’t confident in division, to solve equations.

Applying the area model division in a real-life context

You can apply the division area model to a number of real-life problems, including:

• Sharing a large number of sweets between friends
• Splitting a large bill between people

Equations and formulas in area model division

There is no specific equation or formula for area model division. Instead, we would just use the division formula of dividend = divisor x quotient. Instead of focusing on equations or formulas, we work out our own numbers to take away from the dividend.

Deriving equations using area model division

To derive equations using the area model to divide, we use other operations. Deriving an equation means to answer it using what you know about the numbers or equation. Because we know the multiples of our divisors, we can derive the equation with them.

Area model division with remainders

Area model division can also be done with remainders and you don’t need to change your steps to do this.

Let’s use the area model examples of 294 ÷ 5. We know 5 x 10 = 50, and 5 x 50 = 250. This means we take 5 away from 294 25 times and are left with 44. 5 x 8 = 40, so we’re now left with 4, and we can’t take 5 away from that again. Therefore, 294 ÷ 5 = 58 with the remainder of 4.

Practice problems on area model division

Put your knowledge to the test with our solved area model division problems!

Practice problem 1

Solve 482 ÷ 12.

Answer: 

40 with the remainder of 2.

12 x 10 = 120

120 x 4 = 480

We cannot take 12 away from 2, so our answer is 40 with the remainder of 2.

Practice problem 2

Solve 345 ÷ 15.

Answer: 

23.

15 x 10 = 150

150 x 2 = 300

15 x 3 = 45

10 x 2 + 3 = 23.

Area model division worksheets

Now try out our division area model for 4th grade math worksheets to further your learning!

• Area model multiplication worksheets
• Division worksheets
• Long division worksheets
• Division with remainders worksheets

Frequently asked questions on area model division

What is area model division?

Area model division is a method of division that breaks it up into smaller steps. By subtracting multiples of your divisor from your dividend, you can make the equation easier to solve.

How does area model division work?

Area model division works by breaking a division equation into smaller, more manageable steps and using multiplication and subtraction instead of division.

What are the benefits of area model division?

The benefits of area model division are visualizing and simplifying large and complex division operations. They can give kids who struggle with division more confidence in solving equations.

What are some examples of area model division?

Some examples of area model division can include dividing up sweets amongst friends, or dividing up a bill when you go out to eat.

What are the steps in area model division?

The steps in area model division are:

• Draw a rectangle and write your divisor to the left and your dividend in the middle
• Use multiples of your divisor to subtract from the dividend
• Keep going until you reach 0 or you have a remainder