Base of an Exponent – Definition with Examples
Updated on January 5, 2024
Welcome to another engaging article on the Brighterly website, where we light up the path of knowledge, making learning an adventure for all children. This post focuses on the all-important concept of the base of an exponent in mathematics. Exponents are a significant part of your mathematical journey, whether you’re learning simple multiplication, diving into algebraic expressions, or exploring exponential growth and decay. Exponents have a wide array of applications in various fields, from computer science to engineering and economics. With Brighterly, you’re not just learning math, but the language of the universe.
Our mission at Brighterly is to break down complex concepts into understandable, digestible parts. This post is designed with your needs in mind, offering clear definitions, easy-to-understand examples, and exciting practice problems. Let’s dive in and explore the world of exponents and bases together. The journey might seem challenging at first, but remember, every expert was once a beginner, and Brighterly is here to guide you every step of the way!
What is the Base of an Exponent?
In the vast, varied world of mathematics, one term that often bewilders students is the base of an exponent. By the end of this comprehensive post, your understanding of this concept will significantly improve, and you’ll realize how intriguing this aspect of mathematics can be. Exponents and their bases are integral elements in exponential equations, something you might come across in various mathematical and real-life scenarios. The base of an exponent is the number that is repeatedly multiplied in an exponential expression.
The base is denoted as “b” in an exponential expression “b^n” where “n” is the exponent. The value “b” is the number that’s getting multiplied by itself “n” times. For instance, in the exponential expression 2^4, the number “2” is the base, and “4” is the exponent. This tells us that the number 2 is being multiplied by itself four times (2 * 2 * 2 * 2).
Definition of the Base of an Exponent
Before delving further into examples and properties, let’s formally define the base of an exponent. In an exponential expression, the base is the number that is subject to repeated multiplication. This concept is central to understanding exponential growth and decay, where numbers can increase or decrease exponentially.
Examples of the Base of an Exponent
Let’s consider a few examples to illustrate the base of an exponent. In the expression 5^3, “5” is the base that is multiplied by itself three times (5 * 5 * 5 = 125). In the expression 10^2, “10” is the base, and it tells us that 10 is being multiplied by itself twice (10 * 10 = 100). In a negative base expression, like (-3)^2, “-3” is the base, indicating that -3 is multiplied by itself two times (-3 * -3 = 9).
Properties of the Base of an Exponent
Understanding the properties of the base of an exponent is essential in comprehending more complex mathematical concepts. These properties are the rules that govern how bases and their respective exponents behave in different operations like multiplication, division, and power of a power.
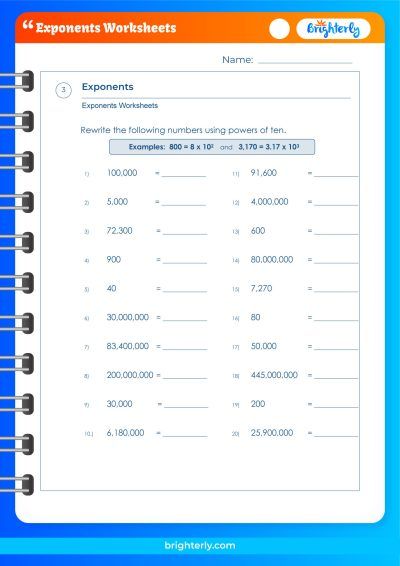
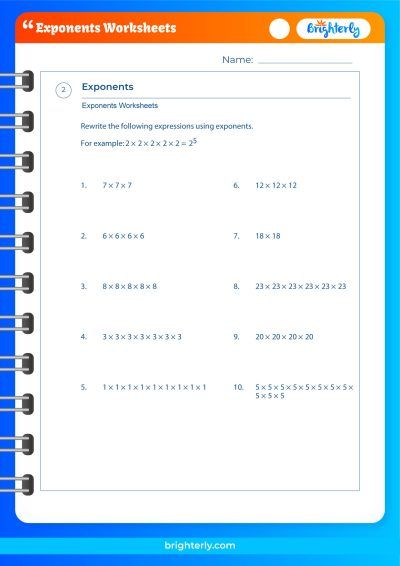
At Brighterly, we believe that practice is the key to mastery. That’s why we invite you to explore our base of an exponent worksheets, where you can find an array of additional practice questions, complete with answers.
Understanding the Base in Different Exponent Types
Positive Exponents
A positive exponent tells us how many times to multiply the base by itself. For example, in 3^4, the number 3 is the base, and the exponent 4 tells us to multiply 3 by itself four times (3 * 3 * 3 * 3 = 81).
Negative Exponents
A negative exponent, like in 2^-3, means we take the reciprocal of the base (1/2 in this case) and multiply it by itself three times ((1/2) * (1/2) * (1/2) = 1/8). So, the base still plays a critical role in determining the outcome.
Fractional Exponents
Fractional exponents, like 4^(1/2), might seem intimidating, but remember, the base “4” is still the number under consideration. In this case, 4^(1/2) is the same as the square root of 4, which equals 2.
Importance of the Base in Exponential Functions
The base in exponential functions determines the rate of growth or decay of the function. For example, in the function y=2^x, the base “2” signifies that y doubles every time x increases by one unit.
Difference Between Base and Exponent
The base is the number that is subject to multiplication, while the exponent tells us the number of times the base is being multiplied by itself. Remember, both the base and the exponent are vital in calculating the result of an exponential expression.
Calculations Involving the Base of an Exponent
Multiplying Exponents with the Same Base
When multiplying expressions with the same base, like 2^3 * 2^4, you add the exponents together while the base remains unchanged (2^(3+4) = 2^7).
Dividing Exponents with the Same Base
When dividing expressions with the same base, like 2^5 / 2^2, you subtract the exponents while keeping the base the same (2^(5-2) = 2^3).
Raising a Power to a Power
In this case, like (2^3)^2, you multiply the exponents while the base stays the same (2^(3*2) = 2^6).
Practice Problems on the Base of an Exponent
-
Simplify the expression 2^5.
Answer: The base here is 2 and we multiply it by itself five times, so 2 * 2 * 2 * 2 * 2 = 32. -
What is the value of 10^3?
Answer: The base here is 10, and we multiply it by itself three times, so 10 * 10 * 10 = 1000. -
Calculate the value of (-3)^4.
Answer: The base here is -3. It’s important to note that the base is negative. We multiply -3 by itself four times, so (-3) * (-3) * (-3) * (-3) = 81. -
Simplify the expression 4^-2.
Answer: The base here is 4, but the exponent is negative. So, we take the reciprocal of the base (1/4) and multiply it by itself twice, giving us (1/4) * (1/4) = 1/16. -
Find the value of 9^(1/2).
Answer: The base here is 9 and the exponent is a fraction, which signifies a root. So, 9^(1/2) is the same as the square root of 9, which equals 3.
Conclusion
Through the journey of this article, we at Brighterly hope that you’ve gained a deeper understanding and appreciation for the concept of the base of an exponent. This mathematical concept, which seemed intimidating at first, should now feel more familiar and accessible. We’ve covered the definitions, worked through examples, and even provided some practice problems to consolidate your knowledge.
Remember, at Brighterly, our aim is to empower learners by demystifying complex topics. Whether it’s the base of an exponent or another exciting mathematical concept, we’re here to guide you. Exponents are not just about numbers and calculations; they’re about understanding patterns, growth, decay, and the incredible world of mathematics.
Stay curious, keep exploring, and remember that learning is a journey. The world of mathematics is vast and beautiful, and this is just the beginning. There’s so much more to explore and learn. After all, that’s the Brighterly way!
Frequently Asked Questions on the Base of an Exponent
What is the base of an exponent?
The base of an exponent is the number that is being multiplied repeatedly in an exponential expression. For example, in 5^3, “5” is the base and it’s being multiplied by itself three times.
How is the base used in exponential expressions?
The base is the number that is being multiplied by itself as many times as the exponent suggests. For example, in 2^4, the base “2” is being multiplied by itself four times.
How are calculations performed with the base of an exponent?
Calculations involving the base of an exponent abide by certain rules. For instance, when multiplying expressions with the same base, we add the exponents. When dividing, we subtract the exponents, and when raising a power to a power, we multiply the exponents.
What role does the base play in exponential functions?
In exponential functions, the base represents the constant factor. If the base is greater than 1, the function grows as the exponent increases. If the base is between 0 and 1, the function decays as the exponent increases.
What’s the difference between the base and the exponent?
The base is the number being multiplied in an exponential expression, while the exponent tells how many times the base is being multiplied by itself.
Information Source:
Math homework help for grade 1-8
Get the homework support your child needs!
Choose kid's grade
Math Program
Boost Your Child's Math Abilities! Ideal for 1st-8th Graders, Perfectly Synced with School Curriculum!
