• Math tutors
• /
• Knowledge Base
• /
• Central Angle: Definition and Practice Problems

Central Angle: Definition and Practice Problems

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on November 13, 2024

At Brighterly, we take the complexity out of math to make learning fun and easy, no matter how challenging you find the subject.

Today, we’re going to be delving into an important geometry concept: the central angle within a circle.

The central angle can divide a circle into sectors and is key to understanding how angles are created within shapes.

Here, we’ll cover the definition of central angle, share examples and the central angle formula, and show you how to calculate the central angle circle. We’ll also give you the tools you need to practice your knowledge, with solved math tasks and free worksheets.

What is a central angle?

A central angle is an angle formed within a circle that meets certain criteria. It is formed by two arms (radii) that intersect with both the edge of the circle and the center of the circle, pointing out from the center in two different directions. We can also work out the central angle of a triangle within a circle if part of the triangle meets the same criteria. We define central angles in full below.

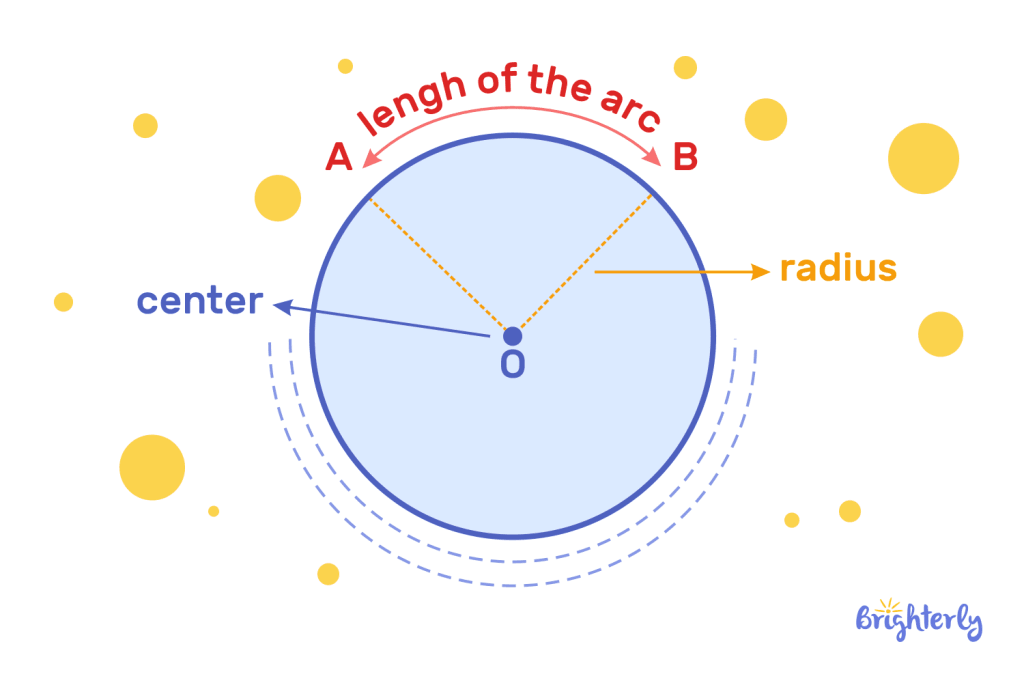
Central angle in geometry: definition

The definition of central angle in geometry is an angle created by two radius lines that intersect both the center of a circle and the edge of the circle. They meet only in the center of the circle and not at any other point. They are completed by the arc of the circle, which creates a shape and therefore the angles of a circle.

Central angle example

Below, we can see an example of central angles in a circle. The central angle, highlighted at point O in red, is created by the two radii (also in red), which reach out from the center of the circle to intersect the edge at two different points.

We can also see that the angle subtended by the arc in the opposite segment of the circle (highlighted in green at point C) is exactly half the size of the central angle. This is what’s known as the central angle theorem, which we’ll provide more detail on later in this article.

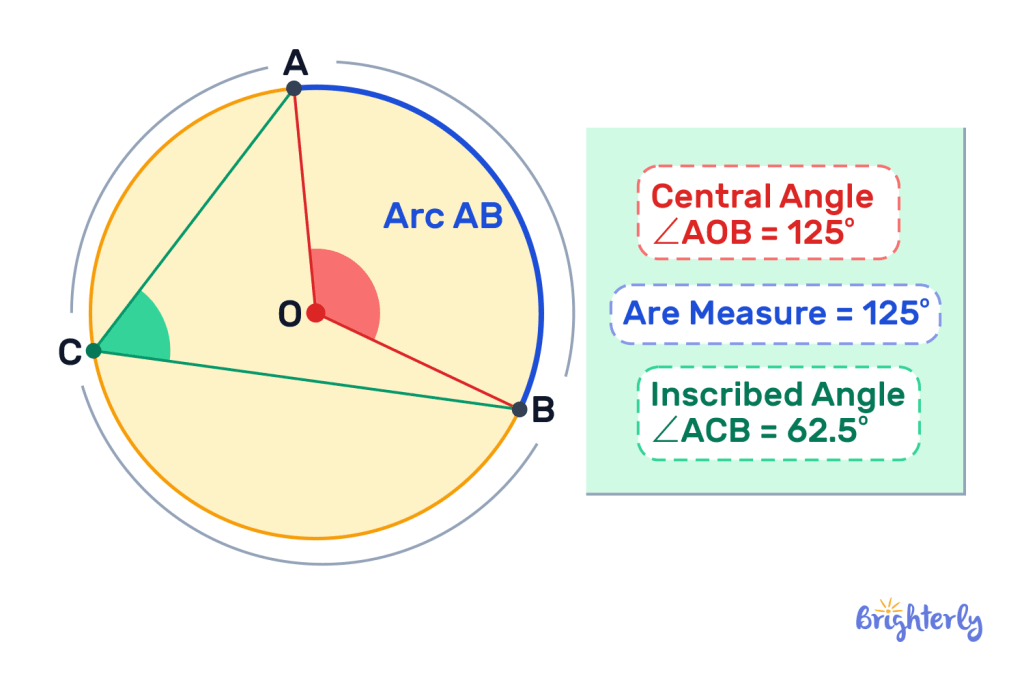
What is a central angle in a circle?

A central angle in a circle is any angle formed when two radius lines intersect the arc of a circle. They create an angle at the center of the circle, hence the name of the central angle in a circle.

Central angle formula

To find the central angle of a circle, you can use the following central angle of a circle formula:

Central angle, θ = (arc length × 360º) ÷ (2π x radius) degrees 

This is often expressed in more simplified terms:

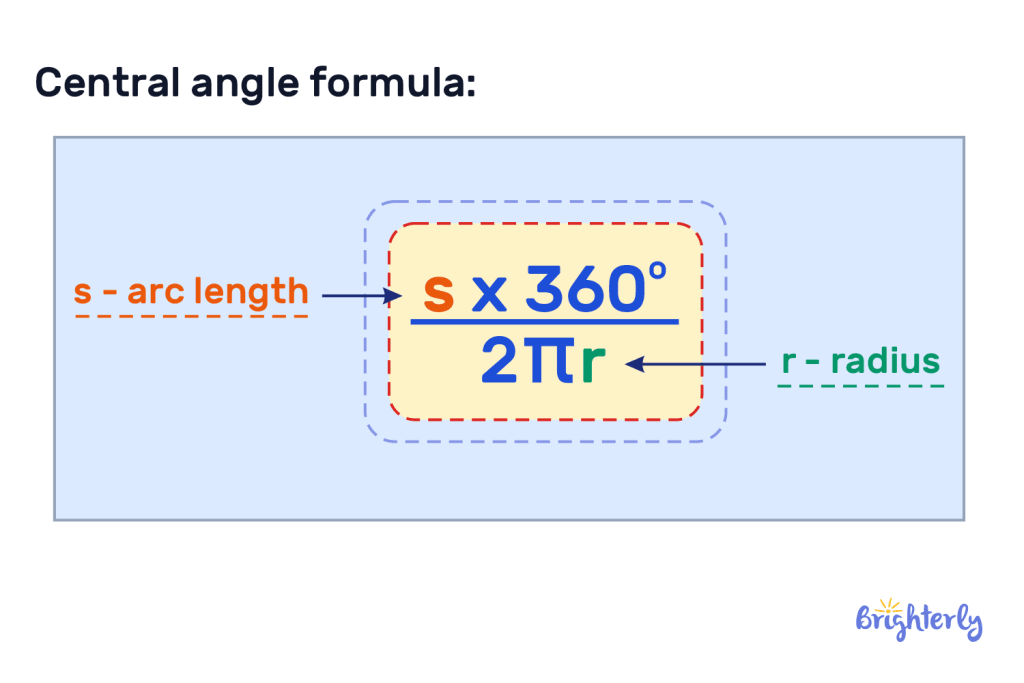
Here, s represents the length of the arc and r represents the radius.

Let’s use an example to help you understand this in more detail. If you have a central angle circle with an arc length of 20 cm and a radius length of 10 cm, our central angle of a circle formula becomes:

(20 cm x 360º) ÷ (2π x 10 cm) degrees

20 cm x 360º = 7,200

2π x 10 cm = 62.83185307179586

7,200 ÷ 62.83185307179586 = 114.5915578477051º

Therefore, our central angle measure is 114.5915578477051º, or 114.59º if we simplify this down to 2 decimal places, which is common mathematics practice.

How to find the central angle of a circle?

All angles can be found by using a protractor. However, if you do not have access to a protractor, you can use the central angle formula stated above to find the central angle of a circle.

You can also find the central angle if you know the size of the inscribed angle – i.e. the angle created in the opposite segment of the circle. This is because of the central angle theorem, which we detail fully below.

Central angle theorem

The central angle theorem dictates the parameters that define a central angle within a circle and can help you understand how angles are created by these radii.

The theorem states that the degree of central angles created by two radii lines will always be twice the size of the angle subtended by the arc in the opposite segment of the circle, i.e. the inscribed angle.

This means that if you know the size of your inscribed angle, you can work out your central angle by doubling it. Conversely, if you know your central angle, you can work out your inscribed angle by dividing your central angle by 2.

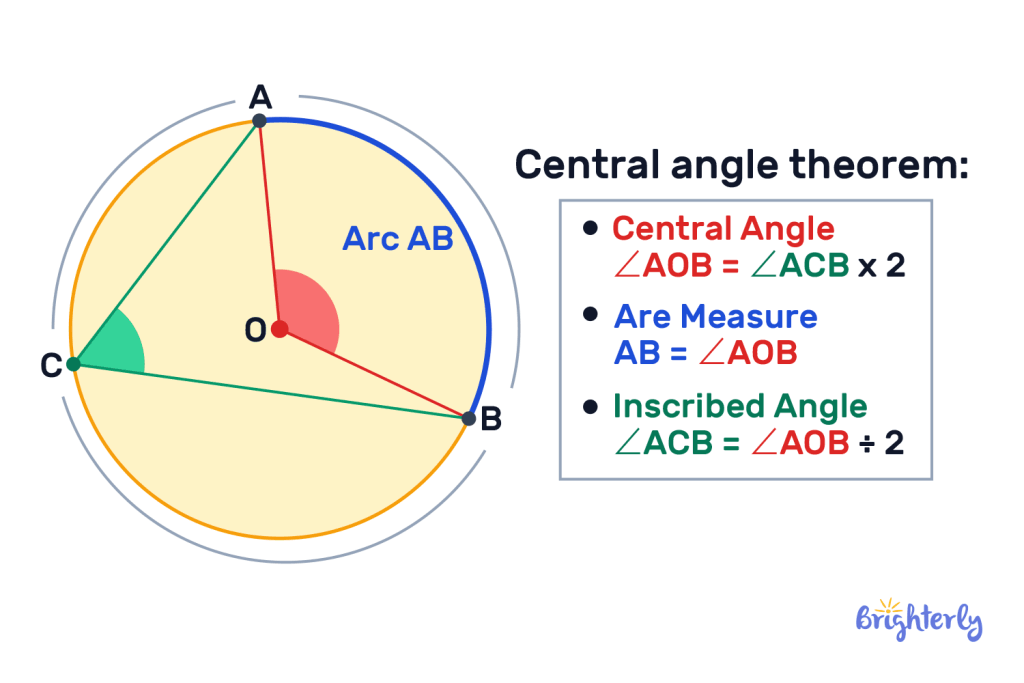
How to find the central angle?

To find the central angle, you’ll need to use the central angle formula as detailed above. It can be helpful to break your formula down into steps to make it easier to solve. However, if you know your inscribed angle, you can also work out your central angle by using that as your base.

For example, if we have an inscribed angle of 70º, we automatically know that our central angle will be 140º because it will always be twice the size of our inscribed angle.

Solved math tasks: examples

Are you confident you can work with the central angle and solve problems related to it? Try out our solved math tasks, then check your answers to see how many of them you’ve got right!

Solved math task 1

Find the angle of a (the inscribed angle) in the below diagram using the central angle of a circle formula or theorem.

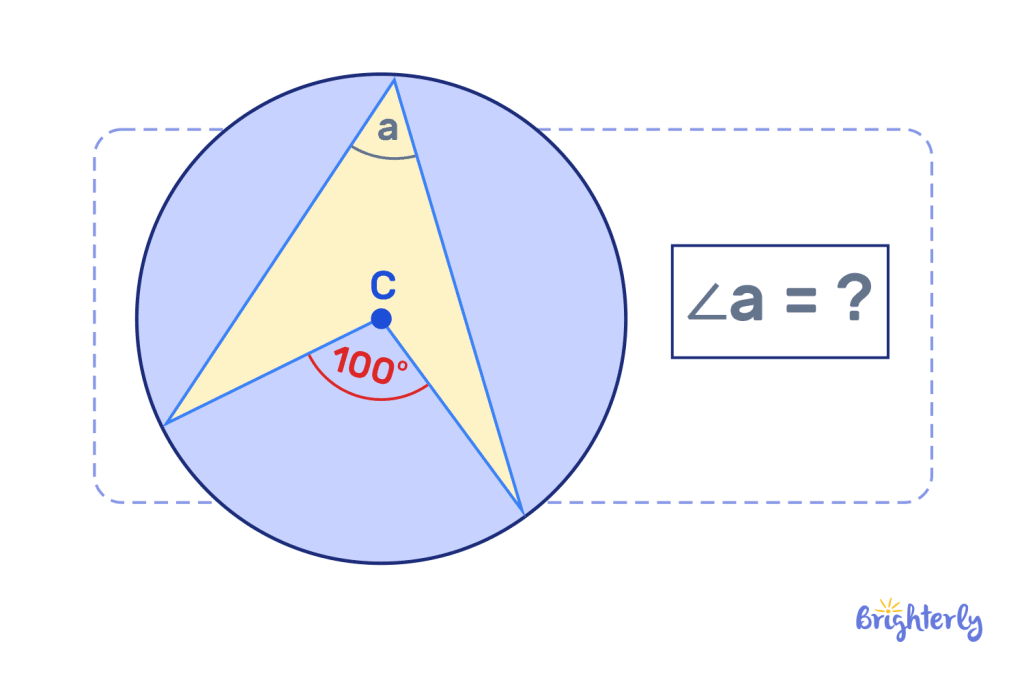
Answer:

We know that the central angle is always twice the size of the inscribed angle. Because we know our central angle here is 100º, all we need to do is half that to get our central angle.

100º ÷ 2 = 50º.

Solved math task 2

You have a central angle with an arc measurement of 12 units and a radii length of 8 units. Using the central angle formula, work out your central angle.

Answer:

12 x 360º = 4,320

2𝜋 x 8 = 50.26548245743669

4,320 ÷ 50.26548245743669 = 85.94366926962348, or simplified to 2 decimal places: 85.94º.

Solved math task 3

Find the angle of h (the central angle) in the diagram below using the central angle of a circle formula or theorem.

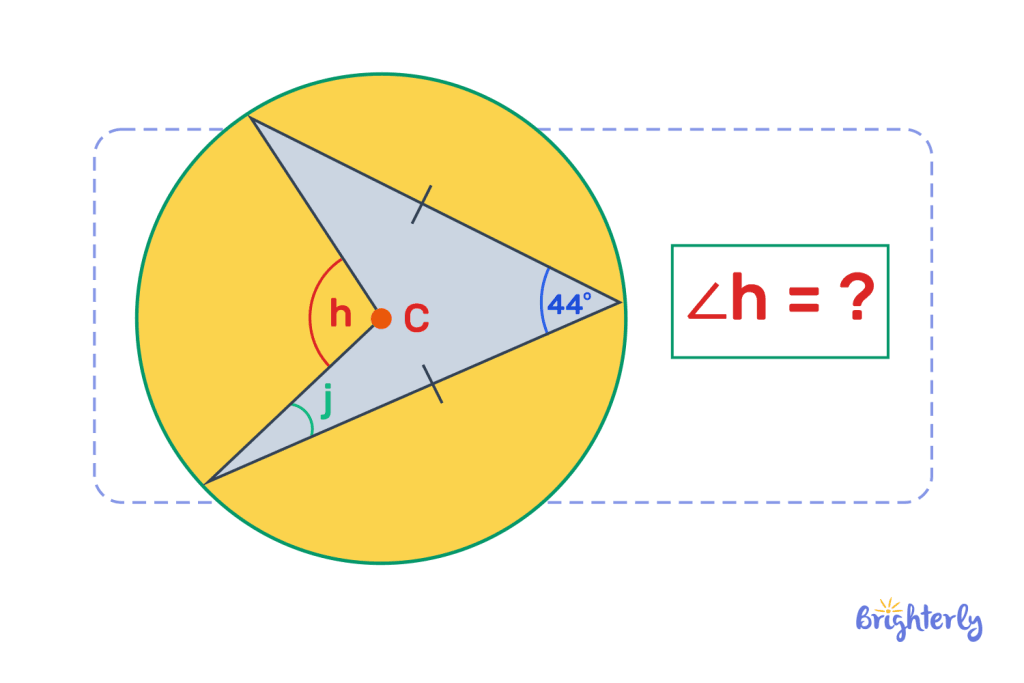
Answer:

We know that the central angle is always double the size of the inscribed angle, so to work out the central angle here, we simply need to double the inscribed angle.

44º x 2 = 88.

Central angle: practice math problems

Central angle: worksheets

Now that you’ve learnt the theory behind the central angle, it’s time to practice and cement your knowledge with our engaging free math worksheets! 

• Trigonometry worksheets
• Lines of symmetry worksheets
• Parts of a circle worksheets
• Circle worksheets

Jessica Kaminski

72 articles

Jessica is a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.