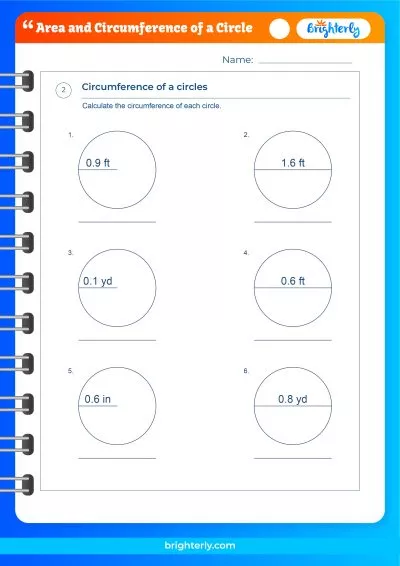
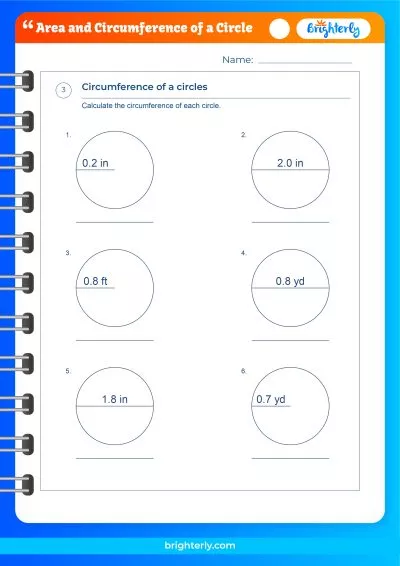
Circumference of a Circle
Updated on January 6, 2024
Welcome to Brighterly, where we make math exciting and engaging for children! Today, we’re going to delve into the fascinating world of circles and explore the concept of circumference. So, fasten your seatbelts as we take you on a mathematical journey!
What is the Circumference of a Circle?
The circumference of a circle is the distance around its outer edge. It is like a magical circle-shaped boundary that contains the entire shape. Imagine taking a piece of string and wrapping it around a circular object – the length of that string would be the circumference of the circle!
Circumference of a Circle Formula
To calculate the circumference of a circle, we use a special formula: C = 2πr, where C represents the circumference and r is the radius of the circle. The Greek letter π (pi) is a mathematical constant approximately equal to 3.14159.
Area of a Circle Formula
While we’re talking about circles, let’s quickly touch upon another important concept – the area of a circle. The formula to find the area of a circle is A = πr², where A represents the area and r is the radius. The area tells us how much space is enclosed within the circle.
Perimeter of Semi-Circle
A semi-circle is a half-circle, cut along its diameter. The perimeter of a semi-circle consists of the straight diameter and half the circumference of the full circle. We can calculate the perimeter using the formula P = πr + 2r, where P represents the perimeter and r is the radius.
Area of Semi-Circle
Similarly, the area of a semi-circle can be found using the formula A = (πr²)/2. It’s like finding half the area of a full circle since we’re only considering one half of the shape.
Enhance your understanding of the circumference of a circle with our comprehensive Circumference of a Circle Worksheets. Access a variety of practice questions, step-by-step solutions, and engaging activities designed to make learning fun. Join us at Brighterly Math for Children and empower young minds to excel in math!
Diameter of the Circle
The diameter of a circle is a line segment that passes through the center of the circle, connecting two points on its circumference. It is the longest possible distance between any two points on the circle. The diameter is precisely twice the length of the radius.
Radius of the Circle
The radius of a circle is the distance from its center to any point on its circumference. It is like the circle’s “halfway point” from the center to the edge. The radius is half the length of the diameter.
How to Find the Circumference of a Circle Using a Thread?
Here’s a fun experiment you can try! Take a circular object and a thread. Wrap the thread around the circle, making sure it hugs the outer edge perfectly. Once the thread completes one full loop around the circle, remove it and measure its length using a ruler. That length is an approximate value of the circle’s circumference!
What is the Circumference to Diameter Ratio?
The ratio of the circumference of a circle to its diameter is constant and denoted by the symbol π (pi). It is an irrational number, meaning its decimal representation goes on forever without repeating. The value of π is approximately 3.14159, but it can be calculated to more decimal places for greater precision in mathematical calculations.
How to Find the Circumference of a Circle?
To find the circumference of a circle, you can use the formula C = πd, where C represents the circumference and d is the diameter. This formula is an alternative way to calculate the circumference, using the diameter instead of the radius.
Circumference to Diameter
The relationship between the circumference and diameter of a circle is simple: the circumference is always approximately 3.14159 (or π) times the diameter. So, if you know the diameter of a circle, you can find its circumference by multiplying the diameter by π.
Practice Questions on Circumference of a Circle
- Find the circumference of a circle with a radius of 5 centimeters.
- Calculate the circumference of a circle with a diameter of 12 meters.
- What is the circumference of a circle if its radius is 10 inches?
- Determine the circumference of a circle with a diameter of 18 feet.
- If the circumference of a circle is 31.4 centimeters, what is its radius?
Take your time to solve these questions, and remember to use the formulas we discussed earlier. Happy calculating!
Conclusion
Understanding the circumference of a circle is not only essential for mathematical knowledge but also for practical applications in everyday life. Whether you’re measuring the perimeter of a circular object or calculating the distance around a track, the concept of circumference plays a crucial role.
By mastering the formulas and concepts related to the circumference of a circle, children can develop their problem-solving skills and mathematical reasoning. At Brighterly, we strive to make math exciting and engaging, empowering young minds to explore the fascinating realm of circles.
So, remember the formula C = 2πr to find the circumference, and A = πr² to calculate the area of a circle. Don’t forget to experiment with threads and objects to visualize the concept firsthand. Embrace the wonders of circles and continue your mathematical journey with confidence and enthusiasm!
Frequently Asked Questions on Circumference of a Circle
Why is the circumference of a circle important?
The circumference of a circle is important because it helps us measure the distance around circular objects. It has practical applications in various fields, such as construction, engineering, and design. Understanding the circumference allows us to accurately calculate dimensions and make precise measurements.
How can I calculate the circumference of a circle if I only know the diameter?
If you know the diameter of a circle, you can calculate its circumference using the formula C = πd, where C represents the circumference and d is the diameter. Simply multiply the diameter by the mathematical constant π (pi) to obtain the circumference.
Can the circumference of a circle be greater than its diameter?
No, the circumference of a circle cannot be greater than its diameter. The circumference is always a multiple of the diameter, and the constant ratio between them is π (pi). The value of pi is approximately 3.14159, meaning the circumference is never more than three times the diameter.
How does the circumference of a circle relate to its radius?
The circumference of a circle is directly related to its radius. The formula to calculate the circumference is C = 2πr, where C is the circumference and r is the radius. The radius is half the length of the diameter, so multiplying the radius by 2π gives us the circumference.
Are there real-life examples that demonstrate the importance of the circumference of a circle?
Yes, the concept of the circumference of a circle has numerous real-life applications. For instance, it helps in determining the amount of fencing needed to enclose a circular garden or calculating the distance covered by a wheel in one revolution. The circumference is also used in fields such as sports, architecture, and transportation to design and measure circular structures and objects.
Remember, at Brighterly, we believe that understanding math concepts like the circumference of a circle opens doors to discovery and problem-solving. Embrace the joy of learning and continue to explore the exciting world of mathematics!
Information Source
Need help with Numbers?
- Does your child need additional assistance with mastering numbers?
- Start learning with an online tutor.
Choose kid's grade
Is your child finding it challenging to understand numbers lessons? An online tutor could be the solution.
