Integers – Definition with Examples
Updated on January 15, 2024
Welcome to Brighterly, your ultimate destination for making math fun and engaging for children! Our mission is to spark curiosity, encourage learning, and demystify the world of mathematics. Today, we’ll explore an essential and intriguing topic in math: integers. In this comprehensive guide, we’ll uncover the secrets of integers, learn about their types, and master the techniques to perform arithmetic operations using them. So, let’s embark on this exciting journey with Brighterly and unlock the power of integers!
What are Integers?
Integers are a vital part of our everyday lives, helping us count, measure, and represent various quantities. In the magical world of mathematics, integers play a crucial role as they provide a foundation for understanding more advanced concepts. Integers can be positive, negative, or even zero, and they can be visualized on a number line. By the end of this Brighterly adventure, you’ll be well-equipped to tackle numerous mathematical challenges involving integers and beyond.
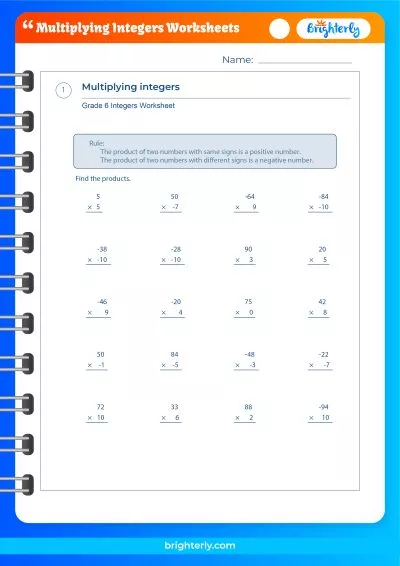
To improve your grasp of the concept of Integers, we recommend exploring the selection of math worksheets offered by Brighterly. These worksheets have been specifically created to aid in learning and strengthening your understanding of this topic.
Integers are a set of whole numbers that include positive numbers, negative numbers, and zero. They can be represented on a number line and are used in a wide range of mathematical operations. Integers play a crucial role in our daily lives, such as counting, measuring, and representing various quantities.
Integers Definition
An integer is defined as a whole number that can be written without a fractional or decimal component. In other words, integers are numbers without any fractional parts. They belong to a larger set of numbers called the integer set, which is represented by the symbol Z.
Types of Integers
There are three types of integers:
- Positive Integers: These are whole numbers greater than zero (e.g., 1, 2, 3, 4…).
- Negative Integers: These are whole numbers less than zero (e.g., -1, -2, -3, -4…).
- Zero: Zero is considered an integer, but it is neither positive nor negative.
How to Represent Integers on a Number Line?
A number line is a straight line with equally spaced points representing different numbers. To represent integers on a number line, follow these steps:
- Draw a straight horizontal line.
- Mark the center point as zero.
- Place positive integers to the right of zero and negative integers to the left.
- Ensure equal spacing between consecutive integers.
How to Perform Arithmetic Operations on Integers?
Integers are used in various arithmetic operations, such as addition, subtraction, multiplication, and division. Let’s explore each operation in detail.
Addition of Integers
When adding integers, follow these rules:
- If both integers have the same sign, add their absolute values and keep the same sign.
- If the integers have different signs, subtract the smaller absolute value from the larger one and use the sign of the larger absolute value.
Multiplication of Integers
When multiplying integers, follow these rules:
- If the integers have the same sign, multiply their absolute values and the result will be positive.
- If the integers have different signs, multiply their absolute values and the result will be negative.
Subtraction of Integers
Subtracting an integer is the same as adding its opposite. So, to subtract one integer from another, add the opposite of the second integer to the first integer.
Division of Integers
When dividing integers, follow these rules:
- If the integers have the same sign, divide their absolute values and the result will be positive.
- If the integers have different signs, divide their absolute values and the result will be negative.
Properties of Integers
Integers exhibit several properties that make them useful in arithmetic operations. These properties are:
- Closure Property: The sum, difference, and product of any two integers will always be an integer.
- Commutative Property: The order of integers does not affect the result when performing addition or multiplication.
- Associative Property: The grouping of integers does not affect the result when performing addition or multiplication.
- Distributive Property: The product of an integer and the sum of two other integers is equal to the sum of the products of the first integer with each of the other integers individually (i.e., a(b+c) = ab + ac). 5. Additive Inverse Property: For every integer ‘a’, there exists an integer ‘-a’ such that their sum is zero (i.e., a + (-a) = 0).
- Multiplicative Inverse Property: For every non-zero integer ‘a’, there exists a unique rational number ‘1/a’ such that their product is one (i.e., a * (1/a) = 1).
- Identity Property: The identity elements for addition and multiplication are zero and one, respectively. Adding zero to an integer does not change its value, and multiplying an integer by one does not change its value either (i.e., a + 0 = a and a * 1 = a).
Examples on Integers
Let’s go through some examples to better understand integer operations:
- Addition: (-3) + 5 = 2
- Subtraction: 8 – (-4) = 8 + 4 = 12
- Multiplication: (-6) * 7 = -42
- Division: (-12) ÷ 3 = -4
Practice Questions on Integers
Now that you have a solid understanding of integers and their operations, try solving these practice problems:
- (-7) + 10 = ?
- 15 – (-3) = ?
- (-5) * (-9) = ?
- 20 ÷ (-4) = ?
Conclusion
Congratulations on completing this captivating journey into the realm of integers with Brighterly! As you’ve discovered, integers are essential building blocks in mathematics and play a significant role in our daily lives. They come in various forms, such as positive, negative, and zero, and can be represented on a number line. By mastering the properties and operations involving integers, you’ve unlocked a treasure trove of mathematical possibilities.
With Brighterly by your side, you’ll continue to uncover the wonders of mathematics and develop a solid foundation to tackle even the most challenging problems. Remember, the world of math is vast and full of exciting discoveries waiting to be made. Keep learning, stay curious, and let the magic of Brighterly guide you through your mathematical journey!
Frequently Asked Questions on Integers
Are all whole numbers integers?
Yes, all whole numbers are integers. Whole numbers include zero and all positive integers. Integers consist of zero, positive whole numbers (also known as natural numbers), and their corresponding negative counterparts. In other words, whole numbers are a subset of integers, representing only the non-negative integers.
Are fractions and decimals considered integers?
No, fractions and decimals are not integers because they have fractional or decimal components. Integers are whole numbers without any fractional or decimal parts. Fractions represent a part of a whole, while decimals represent numbers between whole numbers using a decimal point. Both fractions and decimals are considered rational numbers, as they can be expressed as a quotient of two integers (with the denominator not being zero).
What is the difference between natural numbers and integers?
Natural numbers, also known as counting numbers, are the set of positive whole numbers (e.g., 1, 2, 3, 4…). They are the numbers we use for counting objects or representing quantities greater than zero. On the other hand, integers include positive whole numbers, negative whole numbers, and zero. Integers can represent not only counting and positive quantities but also situations involving negative quantities or a lack of change (zero). In summary, natural numbers are a subset of integers, and the primary difference lies in the inclusion of negative numbers and zero in the set of integers.
Information Sources
For more information on integers, feel free to explore these reliable sources: