Multiplying Exponents – Rules, Definition With Examples
December 19, 2023
8 minutes read
Mathematics is a language, and just like any other language, it has its own set of rules and vocabulary. One of these “words” in the mathematical language that we at Brighterly believe is essential for kids to learn is exponents. But why stop at learning what they are? We find it crucial that children learn how to play with these “words”, especially when it comes to multiplying exponents. Exponents and their operations form the backbone of many advanced mathematical concepts, making it a must-know for every young learner.
This article delves deep into the concept of multiplying exponents, starting from the definition, rules, to providing real-world examples that kids can relate to. This is not just an information source; consider it a simplified guide, especially designed by Brighterly, to help your young ones become proficient with the concept of multiplying exponents. So, without further ado, let’s dive in and discover the world of exponents together!
What Are Exponents?
Exponents, in their simplest definition, are mathematical symbols that represent the number of times a number (base) is to be multiplied by itself. They’re also known as ‘powers’. For instance, in 2^3 (2 raised to the power of 3), the base is 2, and the exponent is 3. This means that 2 is multiplied by itself three times, i.e., 222=8.
The concept of exponents is highly significant in mathematics and can be seen in various topics, including algebra, geometry, and calculus. Understanding exponents is crucial for kids as it serves as a foundation for advanced mathematical concepts.
Definition of Exponents
The exponent refers to the number of times a particular number or variable (the base) is multiplied by itself. For example, in 5^4, the number 5 is the base, and 4 is the exponent. This implies that the base number, 5, is to be multiplied by itself four times: 555*5=625.
It’s also worth noting that any non-zero number raised to the power of zero equals one. For example, 9^0 = 1.
Multiplying Exponents – Basic Rule
When it comes to multiplying exponents with the same base, a simple rule applies. Instead of performing repetitive multiplication, we simply add the exponents together.
Definition of the Multiplication of Exponents Rule
The multiplication of exponents rule states that when you multiply two powers with the same base, you keep the base and add the exponents. In algebraic form, it’s represented as a^(m)*a^(n)=a^(m+n).
So, if you have 2^4 multiplied by 2^3, it simplifies to 2^7, because 4+3 equals 7.
Properties of Multiplying Exponents
The properties of multiplying exponents provide a set of rules that make calculations more comfortable and less time-consuming.
- The Product of Powers Rule: a^(m)*a^(n)=a^(m+n)
- The Power of a Power Rule: (a^m)^n = a^(m*n)
- The Power of a Product Rule: (ab)^n = a^n * b^n
These rules are useful in simplifying complex equations, making them an essential part of algebraic calculations.
Understanding the Multiplication of Exponents Rule
The multiplication of exponents rule allows us to simplify expressions where we are multiplying like bases. Instead of individually calculating each power and then multiplying the results, we add the exponents while the base remains the same.
For example, e 3²* 3 would equal 3^6 instead of calculating (33)(333*3) which would also equal 3^6.
Properties of the Multiplication of Exponents Rule
The properties of the multiplication of exponents rule provide a framework for simplifying algebraic expressions. Here they are:
- When multiplying like bases, add the exponents.
- When raising a power to a power, multiply the exponents.
- When a product is raised to a power, raise each factor to the power.
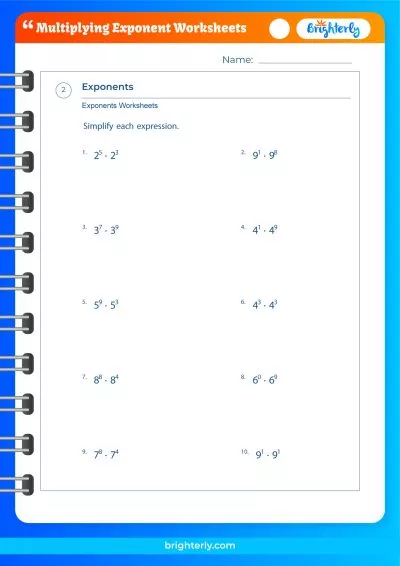
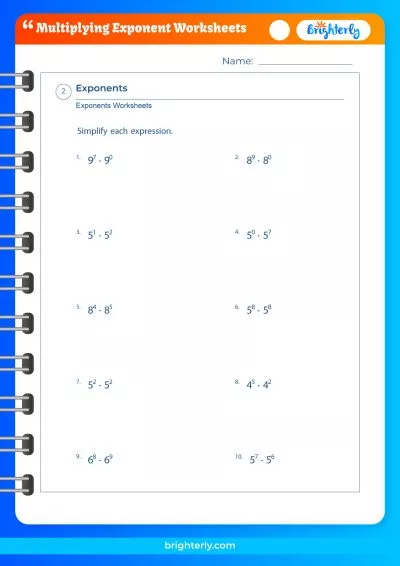
At Brighterly, we believe that practice is the key to mastery. That’s why we invite you to explore our multiplying exponents worksheets, where you can find an array of additional practice questions, complete with answers.
Difference Between Adding and Multiplying Exponents
One of the common misconceptions among students learning exponents is mixing up the rules for adding and multiplying exponents.
Adding exponents happens when you multiply the same base numbers with different exponents (2^3 * 2^4 = 2^(3+4) = 2^7). On the other hand, multiplying exponents occurs when you have a power raised to another power (2^(3*4) = 2^12).
Equations Involving Multiplication of Exponents
Equations involving the multiplication of exponents can look complex, but the rules we’ve learned make them simpler. For instance, the equation (x^3 * y^2) * (x^4 * y^5) = x^(3+4) * y^(2+5) = x^7 * y^7.
Writing Equations Involving Multiplication of Exponents
When writing equations involving the multiplication of exponents, it’s crucial to remember the properties of multiplying exponents:
- Keep the same base and add the exponents when multiplying like bases.
- Raise each factor to the power when a product is raised to a power.
- Multiply the exponents when raising a power to a power.
For instance, the equation for the volume of a cube with sides of length x^3 would be V = (x^3) * (x^3) * (x^3) = x^(3+3+3) = x^9.
Practice Problems on Multiplying Exponents
- Simplify (2^3)^4
- Calculate 3^2 * 3^4
- Solve for (5^3 * 5^2)^2
Conclusion
Understanding and applying the rules of multiplying exponents can initially seem like a daunting task. However, with the right guidance, practice, and a dash of patience, it can become second nature. We at Brighterly believe in making learning enjoyable and effortless, and we hope that this comprehensive guide has brought you one step closer to grasping the concept of multiplying exponents.
Remember, learning is a journey, not a destination. With every step taken, every problem solved, your child is not just learning math; they are developing problem-solving skills, critical thinking abilities, and a knack for logic that will benefit them in every aspect of life. So keep exploring, keep learning, and let Brighterly illuminate the path of knowledge for your young learners.
Frequently Asked Questions on Multiplying Exponents
What does it mean to multiply exponents?
Multiplying exponents means you’re dealing with an operation involving two or more of the same base numbers with different exponents. Instead of multiplying these base numbers individually, we can simplify this process by adding the exponents together. This concept is particularly useful when simplifying mathematical expressions or solving problems that involve repeated multiplication.
What is the rule for multiplying exponents?
The rule for multiplying exponents (also known as the product of powers rule) states that when you multiply two powers with the same base, you keep the base and add the exponents together. So if you’re multiplying 3^4 by 3^2, the result would be 3^(4+2), which simplifies to 3^6. This rule not only makes calculations simpler but also saves a lot of time, especially when dealing with larger exponents.
What is the difference between adding and multiplying exponents?
Adding exponents occurs when you multiply the same base numbers with different exponents. For example, if you’re multiplying 2^3 (2 raised to the power of 3) by 2^4 (2 raised to the power of 4), according to the product of powers rule, you add the exponents together. Hence, 2^3 * 2^4 becomes 2^(3+4), or 2^7.
On the other hand, multiplying exponents happens when you’re raising a power to another power. For example, if you have (2^3)^4, you multiply the exponents together to get 2^(3*4), or 2^12. While both operations involve exponents, the situations in which they are used and the outcomes they produce are different.
Information Source:
Book 1 to 1 Math Lesson
Kid’s grade
After-School Math Program
Boost Your Child's Math Abilities! Ideal for 1st-12th Graders, Perfectly Synced with School Curriculum!
