Prism – Definition, Examples, FAQs
12 minutes read A prism it’s more than just a pretty word. It’s a fundamental concept in the world of geometry, and it’s everywhere around us. At Brighterly, we believe in the power of education to illuminate the world, much like how a prism refracts light into a vibrant spectrum. Through this comprehensive guide, we aim to help children understand and appreciate the intricacies of prisms in a fun and engaging way.
A prism, in its simplest form, is a three-dimensional geometric figure with two identical and parallel faces known as bases. The bases can take the shape of any polygon, opening up a world of prismatic possibilities. Picture a classic Toblerone chocolate bar or the sleek lines of a glass prism refracting a beam of sunlight into a rainbow. These are everyday examples of a triangular prism and a rectangular prism, respectively.
Moreover, the prism is more than just a visual spectacle. It’s a cornerstone of mathematical learning. Its properties and formulas lend themselves to a variety of calculations, enhancing our understanding of space and volume. Understanding prisms is like unlocking a new way of seeing the world. So, let’s embark on this mathematical journey of exploration and discovery. Let’s dive into the captivating world of prisms, illuminated by the light of learning at Brighterly.
What is a Prism?
When you imagine a 3D shape with identical ends and flat faces, what comes to your mind? A Prism. A prism is a polyhedron – a 3-dimensional shape – with two parallel faces called bases that are identical. The other faces, known as lateral faces, are parallelograms formed by connecting the corresponding vertices of the two bases. The bases can be any polygon, but they must be the same on both ends. Prisms are a fascinating part of geometry and play an integral role in our everyday life.
Types of Prisms
Prisms come in a variety of types. The way to categorize them is based on different criteria: the type of polygon of the base, the alignment of the identical bases, and the shape of the bases.
Prisms Based on the Type of Polygon of the Base
Prisms can be named based on the polygon of their base. For example, if the base is a triangle, it’s called a triangular prism. If the base is a square, it’s a square prism (or a cube), and so on. These types of prisms are also known as regular prisms, as their bases are regular polygons – shapes with all sides and angles equal.
Prisms Based on the Alignment of the Identical Bases
A prism can also be categorized by the alignment of its bases. If the bases are directly one above the other and the lateral faces are rectangles, it’s known as a right prism. If the bases are not directly aligned and the lateral faces are parallelograms, then it’s an oblique prism.
Prisms Based on the Shape of the Bases
Another way to classify prisms is based on the shape of their bases. If the bases are polygons with all equal sides and angles, the prism is called a regular prism. If the bases are polygons with unequal sides or angles, it’s an irregular prism.
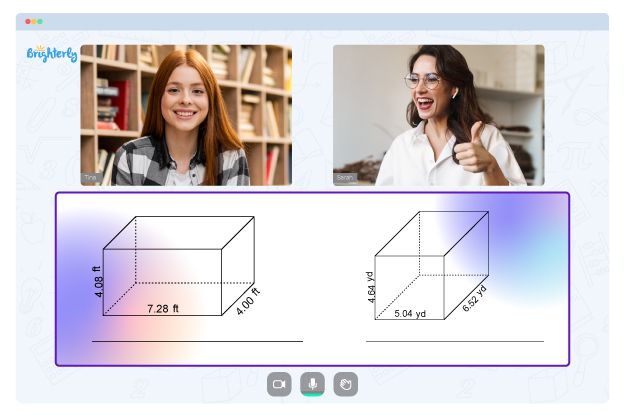
Prisms Formulas
Formulas for prisms can be used to calculate their volume, lateral area, and total surface area. The volume of a prism is given by the formula Volume = Base Area x Height, and the total surface area is given by Total Surface Area = Lateral Area + 2 x Base Area.
Elements of a Prism
Each prism consists of bases, vertices, edges, and faces. The bases are the two identical polygons on the ends. The points where edges meet are called vertices. The edges are the line segments where two faces intersect. The faces include the bases and the lateral faces.
Cross Sections of a Prism
A cross section of a prism is the shape we get when we cut it with a plane. The cross-section of a prism parallel to the bases will be a shape identical to the bases.
Regular and Irregular Prisms
A regular prism has bases that are regular polygons, while an irregular prism has bases that are irregular polygons. In regular prisms, the faces and angles are all equal, while in irregular prisms, they can be different.
Right Prism and Oblique Prism
A right prism has bases that are directly aligned, and its lateral faces are rectangles. An oblique prism has bases that are not directly aligned, and its lateral faces are parallelograms.
Surface Area of a Prism
The surface area of a prism can be calculated using the formula Surface Area = Lateral Area + 2 x Base Area. The lateral area is the sum of the areas of all the faces excluding the bases, and the base area is the area of one base.
Right Prism And Oblique Prism
There’s a distinct difference between a right prism and an oblique prism. In a right prism, the bases are aligned directly above one another and the lateral faces are rectangles. On the other hand, in an oblique prism, the bases are skewed and the lateral faces take the shape of parallelograms.
Prisms Examples
There are many real-life examples of prisms. A box of cereal is an example of a rectangular prism, a tent is often in the form of a triangular prism, and a dice is a cube, which is a type of square prism. These are all right prisms because their bases are directly aligned. Oblique prisms are less common in everyday life but can be found in certain architectural designs.
Practice Questions on Prisms
- Can you name three examples of prisms in your home or classroom?
- If the base of a prism is a pentagon, what is this type of prism called?
- How do you calculate the volume of a prism?
Conclusion
Embarking on a journey through the world of prisms with Brighterly has been a captivating exploration of shapes, mathematics, and the world around us. Prisms, these fascinating three-dimensional figures, are more than just academic concepts confined to the pages of a geometry book. They permeate our daily lives, adding structure, utility, and a dash of geometric beauty to the world we inhabit.
From the cereal box you pour your breakfast from, to the tent you camp in, or even the architectural marvels that punctuate city skylines, prisms shape our world in both mundane and profound ways. Grasping the properties, classifications, and formulas of prisms not only helps us navigate academic challenges but also deepens our understanding and appreciation of the space we occupy.
At Brighterly, we’re committed to shining a light on the beauty of learning, making complex concepts accessible, engaging, and enjoyable for children. By understanding prisms, we empower ourselves with knowledge, illuminate our minds, and see our world from a fresh, enlightening perspective.
Frequently Asked Questions On Prism
What is a prism?
A prism is a three-dimensional geometrical figure that has two identical and parallel faces, known as the bases. These bases can be any polygonal shape, which means they can have any number of sides, from triangles and squares to pentagons or hexagons. The other faces of the prism, known as the lateral faces, are parallelograms or rectangles, and they connect the corresponding sides of the two bases. The prism gets its name from the shape of its base. So, if the base is a triangle, the prism is a triangular prism. If the base is a square, it’s a square prism, and so on.
What are the types of prisms?
Prisms can be categorized based on various properties. One way to classify prisms is by the shape of their base. For example, a prism with a triangular base is a triangular prism, and a prism with a square base is a square prism. Prisms can also be categorized by the alignment of their bases. If the bases are directly aligned over each other, it is a right prism. If they are not, it’s an oblique prism. Additionally, prisms can be classified as regular or irregular. A regular prism has bases that are regular polygons, which means all their sides and angles are equal. An irregular prism, on the other hand, has bases that are irregular polygons, with unequal sides or angles.
How do you calculate the volume of a prism?
The volume of a prism is calculated by multiplying the area of the base by the height of the prism. To do this, you first need to calculate the area of the base. The formula you use for this will depend on the shape of the base. For example, the area of a square is calculated by squaring the length of one of its sides, and the area of a triangle is calculated by multiplying the base by the height and then dividing by two. Once you have the area of the base, you multiply it by the height of the prism to find the volume. So, the formula for the volume of a prism is: Volume = Base Area x Height.
What is the difference between a right prism and an oblique prism?
The key difference between a right prism and an oblique prism lies in the alignment of their bases. In a right prism, the bases are directly aligned, one directly over the other, and the lateral faces (the sides) are rectangles. This means that if you were to draw a line perpendicular to one base, it would hit the center of the opposite base. In an oblique prism, the bases are not directly aligned, and the lateral faces are parallelograms instead of rectangles. This misalignment creates a slant in the sides of the prism, distinguishing it from a right prism.
What is a cross-section of a prism?
A cross-section of a prism is the shape you see when you make a “cut” through the prism. Think of it like slicing through a loaf of bread. The shape of each slice is a cross-section. If you cut a prism parallel to its bases, the cross-section will be a shape identical to the base. This can provide a helpful visual understanding of the structure of the prism. For example, if you have a triangular prism and you slice it parallel to its bases, you’ll see a triangle in each slice or cross-section.
Information Sources:
Struggling with Geometry?
- Does your child need extra support with grasping the concept of geometry?
- Start lessons with an online tutor.
Kid’s grade
Is your child finding it hard to understand the basics of geometry? An online tutor could be of help.
Book a Free Lesson
