• Math tutors
• /
• Knowledge Base
• /
• Properties of Addition – Definition, FAQs, Examples

Properties of Addition – Definition, FAQs, Examples

Jo-ann Caballes

Updated on December 11, 2024

Addition is often the first arithmetic operation that young learners are exposed to. However, despite how easy it is, addition cannot be done except that we follow certain rules. 

These rules are called addition properties.

Here, we learn about the properties of addition through the addition property definition, addition property examples, and practice questions.

What Is Addition?

Addition is one of the four basic arithmetic operations taught at the beginning of our mathematical journey. It is a combination of two or more quantities of a value to determine its new quantity. 

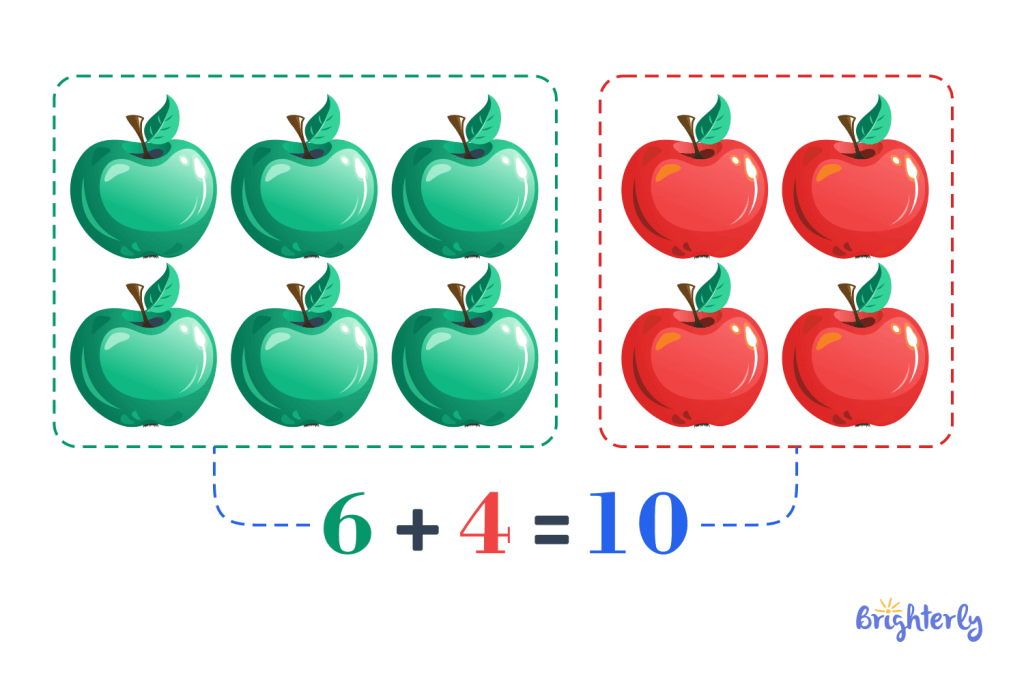
Addition examples

For instance, if we wanted to know how many oranges there are in two different baskets when one basket has 5 and the other has 3, we simply add 5 and 3, resulting in 8. This means there are 8 oranges in total.

We use it every day, everywhere, all the time. When we calculate our bill, we use addition. To know the number of boys and girls in a class, we use addition — and there are so many other examples. 

What are the Properties of Addition?

The properties of addition are a set of guiding rules that apply to all fractions, decimals, and integers in mathematics when using addition. These properties make additions accurate and help us avoid calculation errors.

There are different types of addition, and these rules guide us through the process every time.  Each is unique, but by learning them, you can identify the addition property and their differences.

What are the Five Properties of Addition?

The five (5) guiding addition properties in math or  properties of addition examples are:

• Closure Property of Addition
• Commutative Property of Addition
• Associative Property of Addition
• Additive Identity Property of Addition
• Additive Inverse of Addition

Closure Property of Addition

The closure property of addition states that the sum of two positive integers results in another positive integer.

Positive integers are whole numbers like 1, 2, 3, 4, and so on. An example of this property in action is that 4 + 3 = 7.

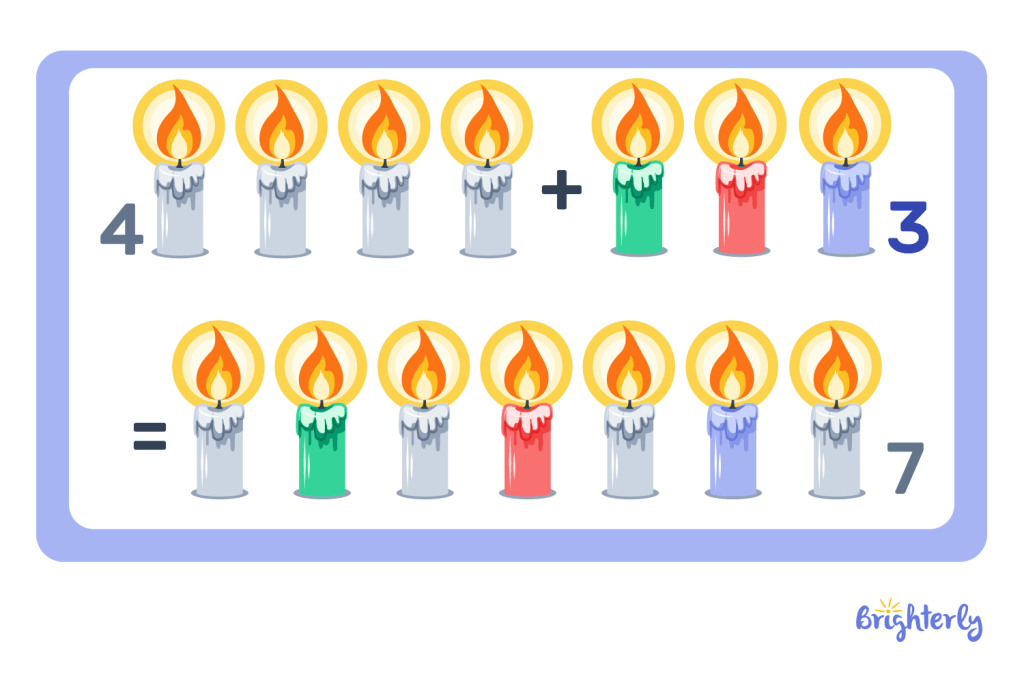
Commutative Property of Addition

The definition of commutative property of addition explains that the result will be the same when summed, regardless of the order in which the numbers are placed.

Therefore, 5 + 8 = 13, the same as how 8 + 5 = 13.

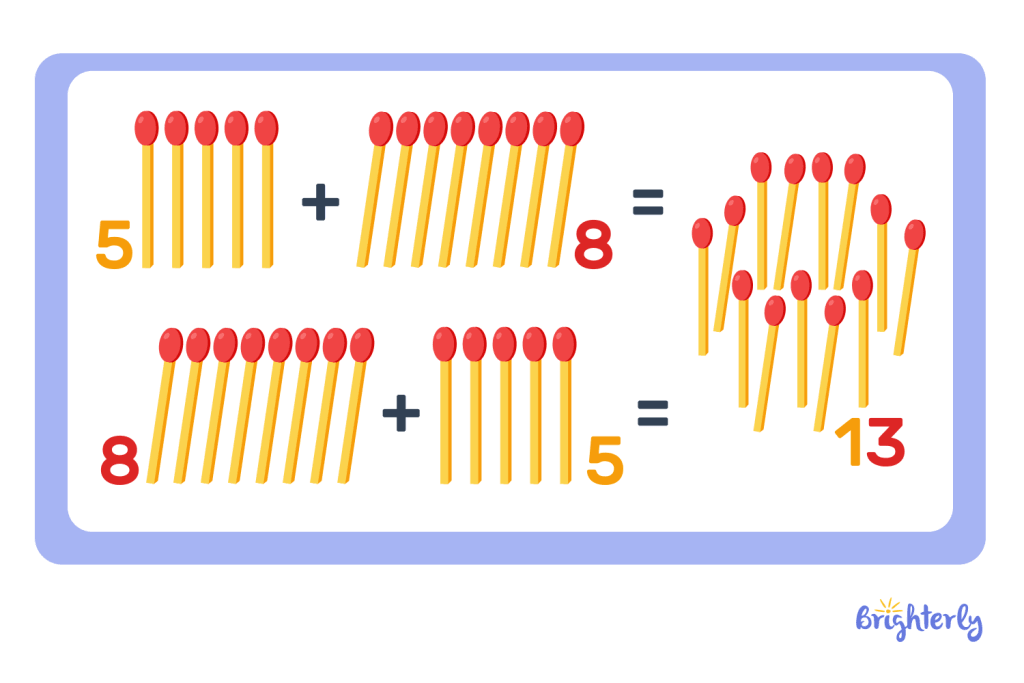
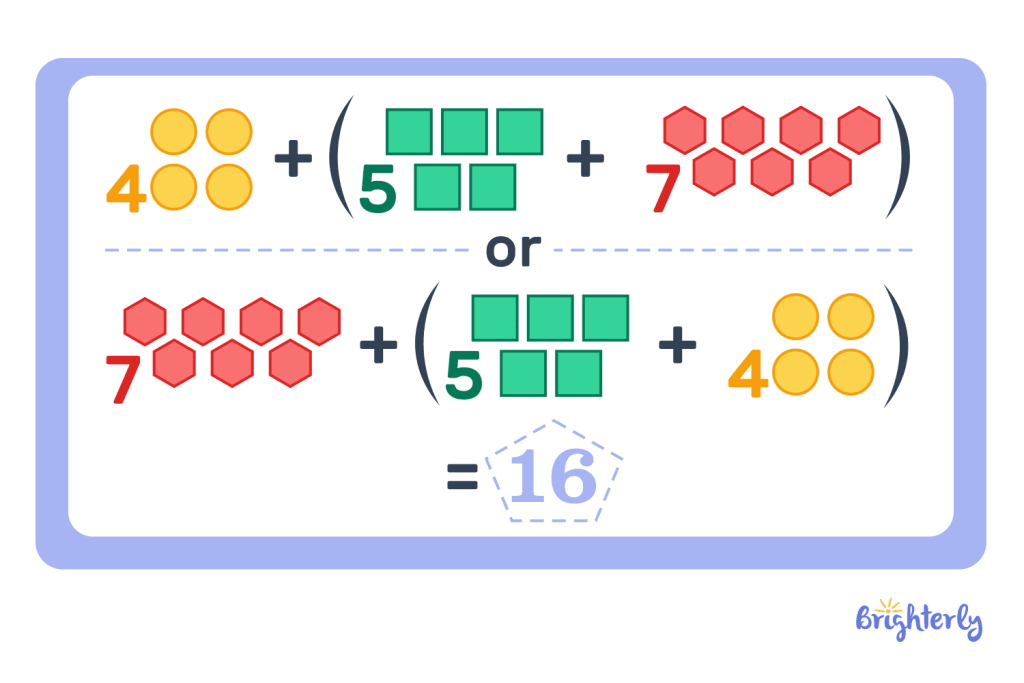
Associative Property of Addition

According to the associative addition property, even when the number of addends is three or more, we can still switch their places and the result will remain the same.

For instance, 4 + (5 + 7) = 16 and 7 + (5 + 4) = 16 are the same. 

Additive Identity Property of Addition

In mathematics, the number 0 is known as the additive identity. This property tells us that whenever we add 0 (additive identity) to a number, the number remains the same. 

This means 56 + 0 + 0 is equal to 56. The value does not change. This additive property is also known as the zero property of addition.

Additive Inverse of Addition

Numbers have inverses and this property states that when we add a positive whole number with its inverse, the result is 0. An example is 7. The inverse of 7 is –7. When we calculate: 7 + –7 the answer is 0.

Math tutors

Improve your child’s math skills today with Brighterly.

Let them be at the top of their class

Try demo lesson now

Solved Examples of Properties of Addition

Solved math problem 1

How does the closure property of addition come into play when Jerry finds 3 marbles in addition to the 4 in his pocket?

Solution

The closure property is applied because since both numbers (3 and 4) are natural numbers, the result is also a natural number.

Solved math problem 2

Jerry wants to add his 7 marbles to Joe’s 8 marbles.  What does the commutative property tell us?

Solution

Solved math problem 3

Maya joins the group of friends with 9 marbles, how can we add Jerry’s 7 marbles and Joe’s 8 marbles per the associative property?

Solution

Solved math problem 4

Which property of addition is shown when Jerry does not add any marbles to his collection of 7?

Solution

The additive property. It explains that the number remains the same when we add 0 to a number. 

Solved math problem 5

What is the additive inverse property of Jerry’s 7 marbles?

Solution

The additive inverse property is the rule that the inverse of any number is the number itself but with an opposite sign, and when it is added to the original number, the answer is 0. 

Practice Problems On Properties of Addition

Frequently Asked Questions On Properties of Addition

What is the Closure Property of Addition?

The closure property of addition is the rule that the sum of any two or three natural numbers (positive whole numbers) will always result in another natural number. 

It is called a “closure” because the addition remains within the positive integer set and the addition does not go out of the set.

Why is the Commutative Property of Addition important?

The commutative property is important because it helps us add numbers without rigidity. This property, therefore, makes it possible to do mental math or add large numbers because we can rearrange the numbers to an order that works best for us. 

How does the Associative Property of Addition help in calculations?

The associative property helps us with complex calculations that are in groups. Since this property states that the answer 9 is the same if we do 3 + (2 + 4) or 4 + (2 + 3), we can solve for answers easier with a process that works for us.

What does the Additive Identity Property of Addition mean?

The additive identity property of addition means that when we add 0 to any number, the number remains unchanged. This property applies to real-life scenarios, too. In a classroom with 12 students, if 0 new students join the class, the number of students will remain 12.

This property and the others are guiding principles that make addition possible.

Jo-ann Caballes

13 articles

As a seasoned educator with a Bachelor’s in Secondary Education and over three years of experience, I specialize in making mathematics accessible to students of all backgrounds through Brighterly. My expertise extends beyond teaching; I blog about innovative educational strategies and have a keen interest in child psychology and curriculum development. My approach is shaped by a belief in practical, real-life application of math, making learning both impactful and enjoyable.