Rate in Math: Unit Rate, Ratio, and Examples
reviewed by Jo-ann Caballes
Updated on November 12, 2024
Have you ever heard someone saying, “the rate at which something happens”?
We use rates to compare and show the relationship between two different concepts. It is an important topic because when we understand the relationship between different concepts, we can analyze trends and make informed decisions.
Here, we explain rate definition in math, rate examples in math and much more. Keep reading!
What is a rate?
A rate is the comparison of two different quantities and units. However, this comparison allows us to see the relationship between them.
Rate Definition In Math
Rate in math is a medium through which we can express the similarities or relationships between two different units.
We signify rates with per or /. These help us to describe units concerning each other.
It should be noted that math rates when expressed are typically something per time such as miles per hour or calories burned per day.
However, rates may be used to compare other types of quantities like 2 cups of sugar per serving, gallons of petroleum per dollar, and so on.
Let’s look at some examples below.
Examples of rates in everyday life
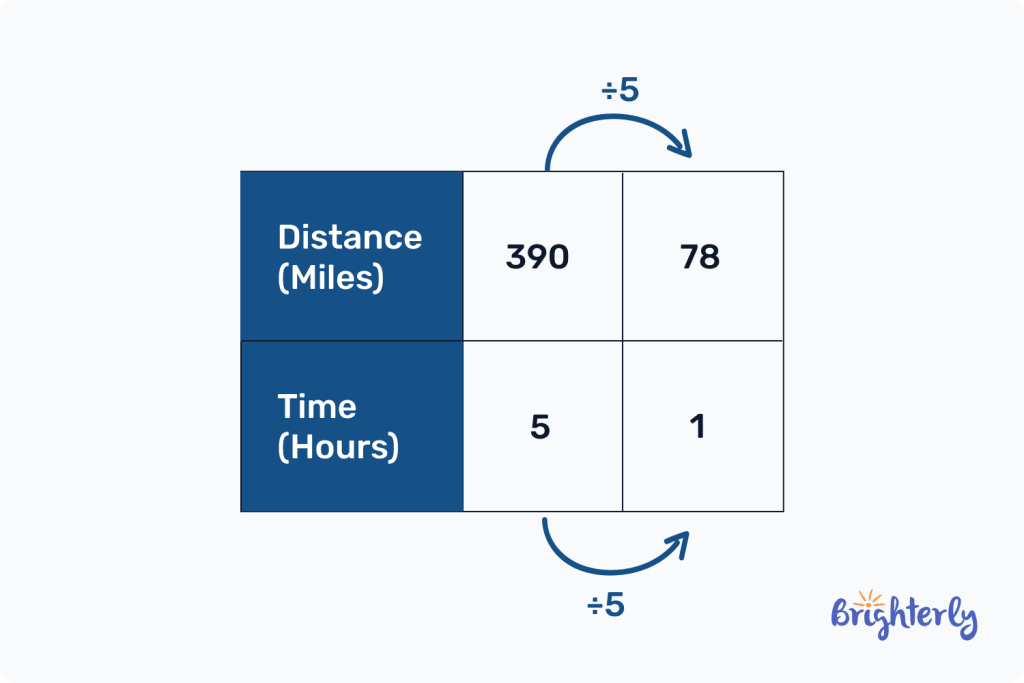
We often use rates on a daily basis even when we don’t notice it. For instance, when we measure how fast a car moves, we may say it moves at a rate of 60 miles per 2 hours.
The use of “per” helps to show the relationship between the car’s speed (30 miles) and the time it moves (2 hours).
Another example of where we use rates is in wages. When applying for a job, they may offer to pay at a rate of $35/hr.
Again, the symbol “/” shows the relationship between $35 and an hour.
How to find rate in math?
To find the rate of two units, we divide one unit by the other. Therefore this is how it would look when changed to a formula:
Rate = quantity 1 / quantity 2
So, if we were to find the rate of flour to sugar when a cooking recipe tells us to put 4 spoonfuls of sugar for every 20 cups of flour, we would:
- Write down the quantities: Quantity 1 = 20 and Quantity 2 = 4
- Write it in the formula given: 20/4
- Divide and simplify the equation: 20/ 4 = 5/1.
This means the rate of flour to sugar is 5 cups of flour to 1 spoonful of sugar.
Unit rate definition in math
Unit rate, like the standard rate, is also used to show the relationship between two quantities, however, with the unit rate, the denominator is always 1.
It’s in the name — unit. The unit rate is used to compare the quantity of something, whether large or small, with a single unit of another thing.
What is an example of a unit rate in math?
An example of a unit rate can be when you work out. Imagine that you manage to burn 3000 calories in 3 hours. This means you can say you burnt 1000 calories per hour when you use unit rate in a sentence for easier comprehension.
Another example is the heart which beats at a rate of 120 times per 2 minutes. If we were to find the unit rate, we would arrive at 60 heartbeats per 1 minute.
Some interesting facts about unit rates are:
- It was used in the early days for calculating trade, for example, 10 handfuls of grain per silver
- With unit rates, we can convert one unit of measurement to another, e.g., the distance of a car from per mile to per foot.
What is Ratio?
Ratio is a method of comparing quantities of the exact units. These quantities, unlike in rate, can be more than two.
For instance, we may compare the quantity of water, sugar, and flour used to bake.
The ratio is represented with a colon symbol “:” and is pronounced as “to” such as 3 : 4: 5, pronounced as 3 to 4 to 5.
Rate and ratio examples and difference
Rate and ratio are both comparisons of units. However, while the rate compares the quantities of different units, the ratio compares the quantities of the same unit.
For the example of a rate, we’d compare the distance a vehicle travels by its speed, e.g., a motorbike that moves at a speed of 75 miles per 3 hours or 75 miles/3 hours.
However, when using ratio, we’d measure something like a class that has 20 boys to 19 girls or 20 boys : 19 girls.
Here are some other differences between rates and ratios:
| Rate | Ratio |
| The symbol for rate is “per” or “/” | it uses “to” or “:” as its symbol |
| it is used to show how one unit is affected by another | It is used to compare parts or the same units. |
| It is mostly the comparison of two quantities | It can be used to compare more than two quantities |
| Example: 75 miles per 3 hours or 75 miles/3 hours | Example: 20 boys to 19 girls or 20 : 19 |
Solved Math Tasks: Examples
Solved math problem 1
At an amusement park, there is a rollercoaster ride that carries 90 people per 3 rides, what is the unit rate?
Answer
The rollercoaster carries 90 people per 3 rides. This is 90/3
= 30/1.
|
Therefore, the unit rate for the rollercoaster is 30 people per ride. |
Solved math problem 2
Molly’s dad buys 4 gallons of petroleum for 14 dollars. How much did he spend on petroleum per dollar?
Answer
14 dollars per 4 gallons of petroleum = 14/ 4 =3.5
|
Molly’s dad spent $3.5 per gallon of petroleum. |
Solved math problem 3
Bridgette buys a new bicycle and is informed that it travels at 120 miles per 10 hours, can you help her find out its actual speed?
Answer
The speed of the bicycle is 120/10 = 12/1
|
Therefore, Bridgette’s bicycle travels at 12 miles per hour. |
Solved math problem 4
Confirm which of the following statements is true or false:
- Ratio and rate are the same thing and can be used interchangeably
- Rate is expressed with a column (:)
Answer
|
Solved math problem 5
The wage of a fast-food worker is $22 per hour. How much does he get paid in a 5-day workweek after working 8 hours each day?
Answer
If he works $22/ hour, to get the equivalence in 8 hours, we would multiply both quantities by 8:
$22 × 8 = $176
1 hour × 8 = 8 hours
This means he gets paid $176 per 8 hours. Next, to get the result in 5 days, we multiply by 5, which is:
$176 × 5 = $880
8 hours × 5 = 40 hours
| Thus, the wage of the fast food worker is $880 per 40 hours or $880 in a 5-day workweek where he works 8 hours a day. |
Rate in Math: Practice Math Problems
Rate in Math: worksheets
Young children need to understand the concept of rate to know how to compare. It helps them find the relationship between seemingly unrelated concepts such as time and speed, or even cooking and washing. With this skill, inferences can be drawn and their decision-making skills can improve.
In this article, we define rate in math and help kids understand the meaning of rate in math. Learn more about rates in math with Brighterly’s free worksheets:
Math homework help for grade 1-8
Get the homework support your child needs!
Choose kid's grade
Math Program
Boost Your Child's Math Abilities! Ideal for 1st-8th Graders, Perfectly Synced with School Curriculum!
