Subtraction Property of Equality – Definition with Examples
reviewed by Jo-ann Caballes
Updated on November 28, 2024
Welcome to Brighterly, where we help you learn a range of math concepts – even the ones you find daunting!
Today, we’re going to explore the concept of the subtraction property of equality.
This principle relates to the operation of subtraction and equations, and how it can help us understand the way values relate to one another.
In this article, we’ll cover the definition of the subtraction property of equality, its formula, how to verify it, how to use it with fractions and subtraction property of equality examples. We’ll also share fun math worksheets and practice test problems so you can improve your knowledge!
What is the subtraction property of equality?
The subtraction property of equality is a principle in math that relates to equations that use subtraction. It can be considered an extension of the addition property of equality, which relates to addition operations. It is also linked to the subtraction property of inequality, which states removing the same number from both sides of an equation does not change the inequality. We use the properties of subtraction to understand how equations can remain balanced. We cover the full definition below.
Subtraction property of equality definition
The subtraction property of equality says that if you have an equation with two sides and you subtract the same number from both sides, they will still remain equal. It can be expressed as a formula:
If a = b, then a – c = b – c.
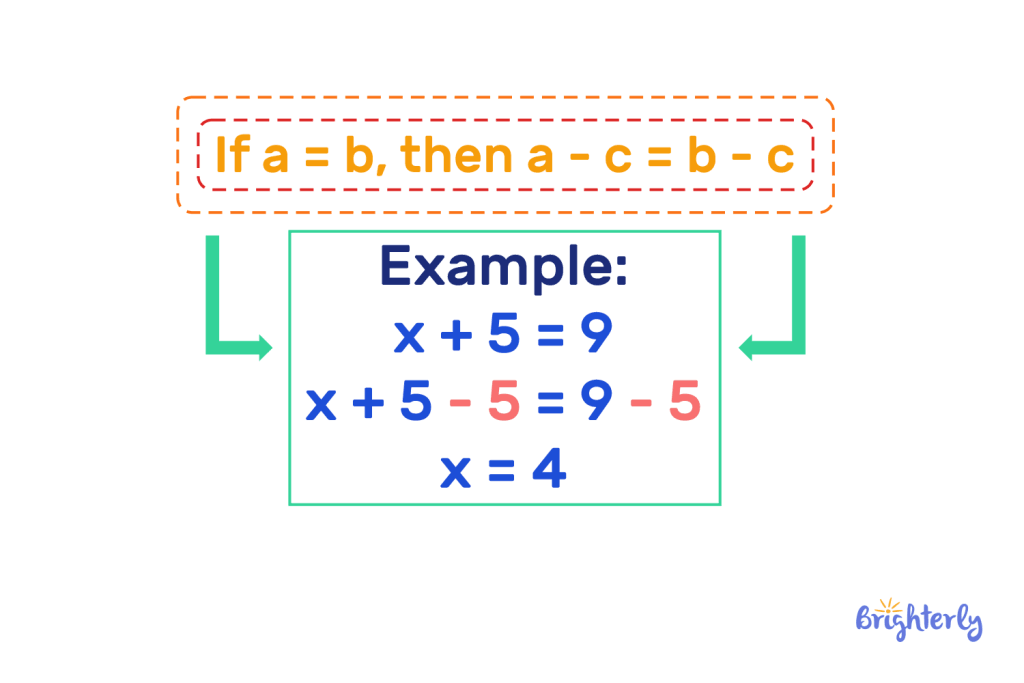
Subtraction property of equality example
It’s helpful to use a subtraction property geometry example to illustrate this principle properly.
We have the equation 5 + 6 = 11, and we need to subtract 3 from each side.
Side 1: (5 + 6) – 3 = 8
Side 2: 11 – 3 = 8
We can see here that after subtracting the same number from both sides of the equation, it remains balanced and equal. This means our example of subtraction property of equality has shown it to be true.
Subtraction property of equality formula
The subtraction property of equality geometry can be expressed in a simple formula:
If a = b, then a – c = b – c.
Because both sides of an equation are equal – i.e. you add two numbers to make a third number – we are saying that subtracting the same number from both sides will keep those sides equal to each other.
Verification of subtraction property of equality
So, how do we verify that the subtraction property of equality works? It’s really simple! All we need to do is pick an equation and subtract the same number from both sides. Every time you do this, you’ll see that the outcome is equal. This means you’ve verified the subtraction property of equality!
Let’s take subtracting 6 from each side of this equation: 5 + 12 = 17.
(5 + 12) – 6 = 11
17 – 6 = 11
Both sides are still equal, so we’ve verified the principle.
Subtraction property of equality including fractions
We can also apply the subtraction property of equality to fractions! Let’s say we have the equation ⅖ + ⅖ = ⅘ and we want to subtract ⅕ from each side.
(⅖ + ⅖) – ⅕ = ⅗
⅘ – ⅕ = ⅗
We can see that our fractions on both sides of the equations are still equal. This shows that we can also use this principle with fractions.
Practice problems on subtraction property of equality
Are you ready to practice your learning on the subtraction property of equality geometry? Try out our practice problems!
- Solve x – 7 = 15.
- If a – b = c, find the value of b in the equation 2a – 3b = 5c.
- Solve 4 – (2x – 5) = 1 + (3x – 2)?
Subtraction property of equality: worksheets
Are you ready to put your subtraction property of equality geometry to the test? Try out our cool worksheets, which focus on the foundational skills needed to master this concept.
- Subtraction worksheets
- Subtraction word problems worksheets
- Subtraction without regrouping worksheets
- Subtraction with borrowing worksheets
Frequently asked questions on subtraction property of equality
What is the subtraction property of equality?
The subtraction property of equality is a mathematical principle that helps us to solve equations and understand how numbers interact with one another. It states that if you have an equation with two sides and you subtract the same number from each side, they will still be equal.
Can the subtraction property of equality be applied to fractions?
Yes, the subtraction property of equality can be applied to fractions! You would take the same steps in an equation with fractions as you would in an equation with whole numbers. If you have an equation with unequal fractions, it’s best to make them equal first to make your equation more straightforward.
How can I verify the subtraction property of equality?
We can easily verify the subtraction property of equality by choosing any equation and subtracting the same number from both sides of the equation. If your final equation is still balanced and both sides are still equal, you’ve verified the subtraction property of equality.
Are there any limitations to the subtraction property of equality?
There aren’t any limitations to the subtraction property of equality. However, in order for it to function correctly, you need to follow the correct steps and apply them accurately in equation manipulations. Take extra care with complex equations, because you may be required to perform multiple operations.
What is a subtraction property of inequality example?
The most basic subtraction property of inequality example is represented by variables.
If a > b, then this must mean that a – c > b – c.
Similarly, if a < b, then this must mean that a – c.
Subtraction property of equality: practice math problems
Struggling with Subtraction?
- Is your child finding it challenging to understand subtraction lessons?
- An online tutor could be the solution.
Choose kid's grade
Does your child struggle to master subtraction lessons? Try lessons with an online tutor.
