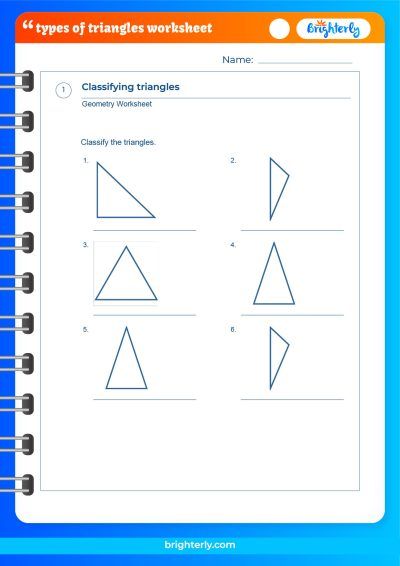
Types of Triangles – Definition With Examples
reviewed by Jo-ann Caballes
Updated on October 8, 2024
Despite their apparent simplicity, triangles are among the most significant geometric shapes. Therefore, recognizing and classifying the many types of triangles is crucial for solving many practical difficulties.
It is also a task most students will learn to handle in grade school, irrespective of their institution’s curriculum. So, in this article, we will cover how to categorize triangles based on the lengths of their sides, their angles, and the measurement of sides and angles.
What Is a Triangle?
A triangle is a simple polygon consisting of three vertices and three edges. A triangle with three vertices, P, Q, and R, represents △PQR.
In geometry, this shape is flat and geometric with three sides and three angles. Some common examples of triangles are signboards and pizzas.
Basic Properties of Triangles
Having seen the types of a triangle, the following is a list of a triangle’s key characteristics.
- A triangle has three vertices, three sides, and three angles.
- A triangle’s interior angles always form a right angle when added together. The triangle’s angle sum attribute describes this.
- When added together, any two of a triangle’s sides are longer than the third.
- The longest side is the one that lies opposite the greatest angle.
- The external angle, the exterior angle of a triangle, is always equal to the sum of the interior opposite angles, according to the triangle theorem.
Types of Triangles
Triangles are more than just random or abstract shapes discussed in a classroom. They are popular in construction because of their stability and seeming rigidity. Understanding these characteristics enables us to use the rules of creating a triangle in several practical problems.
What are the Different Types of Triangles?
Triangles are categorized according to the length of their sides and the measure of their angles. Once we grasp these characteristics and see the examples of triangles, we may use the concepts to solve various practical issues.
What Is the Classification of Triangles?
Side and angle measurements allow for categorizing the different types of triangles. With that in mind, there are three methods of categorization:
- Based on the lengths of the three sides
- Based on the measurement of three angles
- Based on the measurement of sides and angles
Types of Triangles Based on Sides
By looking at triangles with their side lengths in mind, we can identify three types of triangles:
- Equilateral Triangle
- Isosceles triangle
- Scalene triangle
The variety and beauty of these basic shapes are brought to light in each category, giving rise to new insights into the fascinating study of triangles.
Types of Triangles Based on Angles
There are 3 types of triangles distinguished by their angles:
- Acute Triangles
- Right Triangle
- Obtuse Triangle
Classification of Triangles Based on Side Lengths
Triangles types based on the size of their sides are: equilateral, isosceles, and scalene.
Scalene Triangles
Each of the three sides of a scalene triangle is of a distinct length, and the measurements of the three angles vary. In any case, it sums at 180 degrees for the internal angles. Thereby, it satisfies the triangle’s angle sum property.
Isosceles Triangles
Two sides of an isosceles triangle are of the same length. When a triangle is isosceles, the angles on each side are equal.
Equilateral Triangles
An equilateral triangle has three equal-length sides. As a result, the interior angles of equilateral triangles are all 60 degrees. As its name implies, it is a regular polygon with equal sides and angles.
Classification of Triangles Based on Interior Angles
There are three kinds of triangles based on the interior angles: acute, right, or obtuse.
Acute Triangles
The three internal angles of a triangle must be acute for it to be called an acute triangle or an acute-angled triangle. Because of this, we can see that no two of the angles are exactly 90 degrees. The total of the three acute angles in this kind of triangle is always 180 degrees.
Since all of the angles of the triangle are acute, it may adopt several shapes, including isosceles or equilateral, and is hence considered one of the most fundamental triangles in geometry.
Right Triangles
An interior angle of a right triangle must be precisely 90 degrees for the shape to be considered right-angled. In right triangles, the unique relationship between the hypotenuse (the side opposite the right angle) and the other two sides is given by the Pythagorean theorem, which states that, in such a triangle, the square of the hypotenuse’s length is equal to the sum of their squares.
Trigonometry relies heavily on right triangles, which have several real-world applications in fields as diverse as physics, engineering, and architecture.
Obtuse Triangles
When one of the interior angles of a triangle is larger than 90 degrees, we say that the triangle is obtuse or obtuse-angled. The triangle stands out from acute and right triangles due to its obtuse angle.
In conjunction with the other two acute angles that make up an obtuse triangle, the obtuse angle will always equal 180 degrees. Depending on the lengths of its sides, obtuse triangles may be further divided as isosceles or scalene. Many branches of mathematics, particularly geometry and trigonometry, rely on the features and qualities of obtuse triangles.
The table below shows the types of triangles based on sides and angles
| Side Classification | Angle Classification | Triangle Type |
| Scalene | Acute | Acute Scalene |
| Scalene | Right | Right Scalene |
| Scalene | Obtuse | Obtuse Scalene |
| Isosceles | Acute | Acute Scalene |
| Isosceles | Right | Right Scalene |
| Isosceles | Obtuse | Obtuse Scalene |
| Equilateral | Acute | Equiangular |
More about types of Triangle Based on Both Sides and Angles
Equilateral or Equiangular triangles have all sides equal, with the angles being 60 degrees each. This is the easiest triangle for younger pupils to remember and the type they instinctively try to draw when asked to draw a triangle.
On the other hand, the Isosceles triangle only has two sides equal. If we are classifying them based on angles, the acute Isosceles triangle has angles that are all less than 90 degrees. In contrast, one angle is greater than 90 degrees for the Obtuse Isosceles triangle.
For the Scalene triangle, all sides are of different lengths, and all the angles can either be less than 90 degrees (Acute Scalene triangle), one angle can be exactly 90 degrees (Right scalene triangle), or One angle can be greater than 90 degrees (Obtuse Scalene Triangle).
Classification of Triangles Based on Angles and Sides: Summary
There are over 6 different types of triangles based on their sides and angles.
Equilateral or Equiangular Triangle
Equilateral or equiangular triangles are those whose sides and angles are precisely equal. Because various types of angles in these triangles are sixty degrees, they are symmetrical and balanced.
Isosceles Triangle
Isosceles triangles are right triangles with two equal sides and a single right angle measuring 90 degrees. In an isosceles right triangle, the two equal sides create a right angle, while the two acute angles are 45 degrees each.
Obtuse Isosceles Triangle
If a triangle has two equal sides and an obtuse angle on one, we say it is an obtuse isosceles triangle.
Acute Isosceles Triangle
A right triangle with three acute angles and equal lengths on each side is called an acute isosceles triangle. The third angle is similarly acute, and the first two are the same size.
Right Scalene Triangle
A triangle with an uneven length on all three sides and an acute angle is a right scalene triangle. The absence of perfectly equal sides and angles gives this triangle its distinctive asymmetry.
Obtuse Scalene Triangle
An obtuse scalene triangle is a kind of triangle that has an obtuse angle and asymmetrical sides.
Acute Scalene Triangle
An acute scalene triangle is a kind of triangle with three sharp angles and three unequal sides.
Solved Math Tasks: Examples
Below are some solved practice problems on types of triangles.
Example 1: Given that ∠A = 100° and ∠B = ∠C in an isosceles triangle ABC, determine the measure of ∠C.
Solution:
| ∠A + ∠B + ∠C = 180° |
So, ∠B + ∠C = 180° – 100° = 80°
Since ∠B = ∠C, measure of ∠C = 80° ÷ 2 = 40°
Example 2: Determine the kind of triangle using the characteristics of triangles, given that the measure of the angle at the vertices of a triangle is 60 degrees.
Solution:
A triangle with all angles measuring 60 degrees is an equilateral triangle. An equilateral triangle is one in which all the interior angles are the same, measuring 60 degrees each. In this case, the sum of all the angles of the triangle is 180 degrees.
Types of Triangles: Practice Math Problems
Types of Triangles worksheets
Below are some examples of triangles worksheets you can use to help your kids learn.
- Missing angles in triangles worksheets
- Triangle worksheets
- Types of triangles worksheets
- 30-60-90 triangle worksheets
Need help with Geometry?
- Is your child having trouble understanding the basics of geometry?
- An online tutor could provide the necessary assistance.
Choose kid's grade
Does your child struggle to master geometry concepts? Try learning with an online tutor.
