Unit Circle With Tangent – Definition With Examples
Updated on December 19, 2024
Here, we will explore the concepts of unit circle and tangent individually, then discuss how these two can intertwine in the world of trigonometry.
What Is the Unit Circle and Tangent?
The unit circle has a single unit as its radius. The tangent, on the other hand, is one of the three basic trigonometric functions (sine, cosine, and tangent) that help us understand and solve problems relating to an angle.
Definition of the Unit Circle
The unit circle is a radius of one unit. This means that if we draw a line from the center of a circle to any point in the circle, we get one unit.
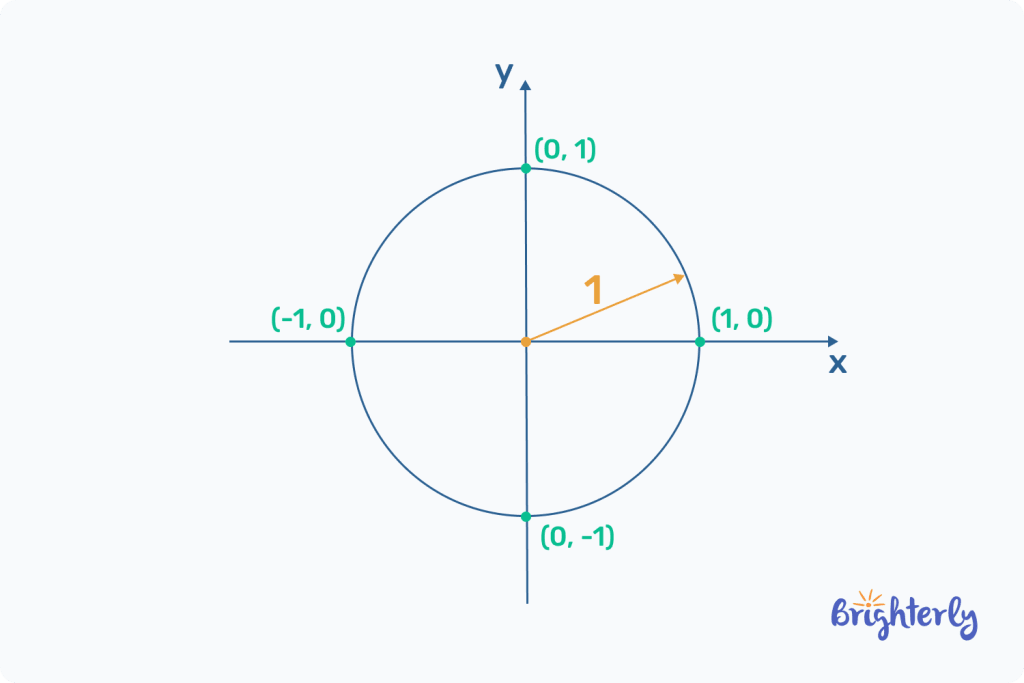
As we will see in this article, this type of circle is the most suitable for understanding angles, trigonometry, and tangents.
Definition of Tangent
A tangent is a line that intersects with a circle at a specific point without touching it again at another. At the place of contact with the unit circle, it forms a right angle (90 degrees) with the radius.
How to find tan on unit circle?
For the unit circle, the tangent is the division of two trigonometric functions of the circle (the sin and the cos).
The sin is the y-coordinate of the circle and the cos is the x-coordinate.
Therefore,
Tangent = sin/cos
Properties of the Unit Circle and Tangent
Let’s explore the properties of each concept to understand their relationship better.
Properties of the Unit Circle
The properties of the unit circle include:
- The circle has a single unit for the radius
- All the points in the circle can be measured in angles as sine and cosine (x, y)
- The x-coordinate is the cosine of the angle and the y-coordinate is the sine of the angle
- The angles in the unit circle are either 360 degrees or 2π radians
Properties of Tangent
- The tangent is a line that touches the circle at a point
- The tangent only touches the exterior of the circle and not the interior
- At the point of contact of the line and the circle, a right angle is formed
- A circle can have more than one tangent, meaning there can be a unit circle with tangents
Relationship Between the Unit Circle and Tangent
We may express the standard angles from 0° to 360° of the unit circle with tangent. This is a different way of measuring the unit circle from the typical use of sine and cosine. We arrive at the tan value by dividing the sine by the cosine, or the y-coordinate by the x-coordinate.
Chart of the Unit circle with Tangent
To make the conversion process easier, use the unit circle table below. It contains the values of sine and cosine as they are converted from degrees and radians.
Here is the unit circle chart with sin cos tan
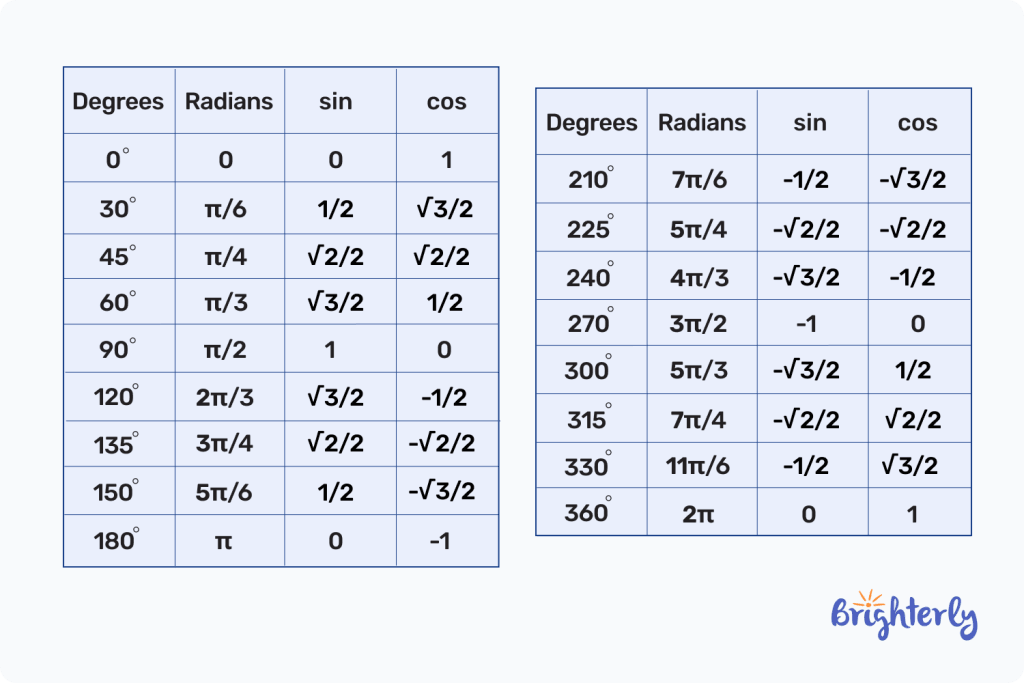
Next, we convert the sine and cosine to tangent by dividing the values of both. Here is the unit circle chart for tan. It contains details about the unit circle with tangent values:
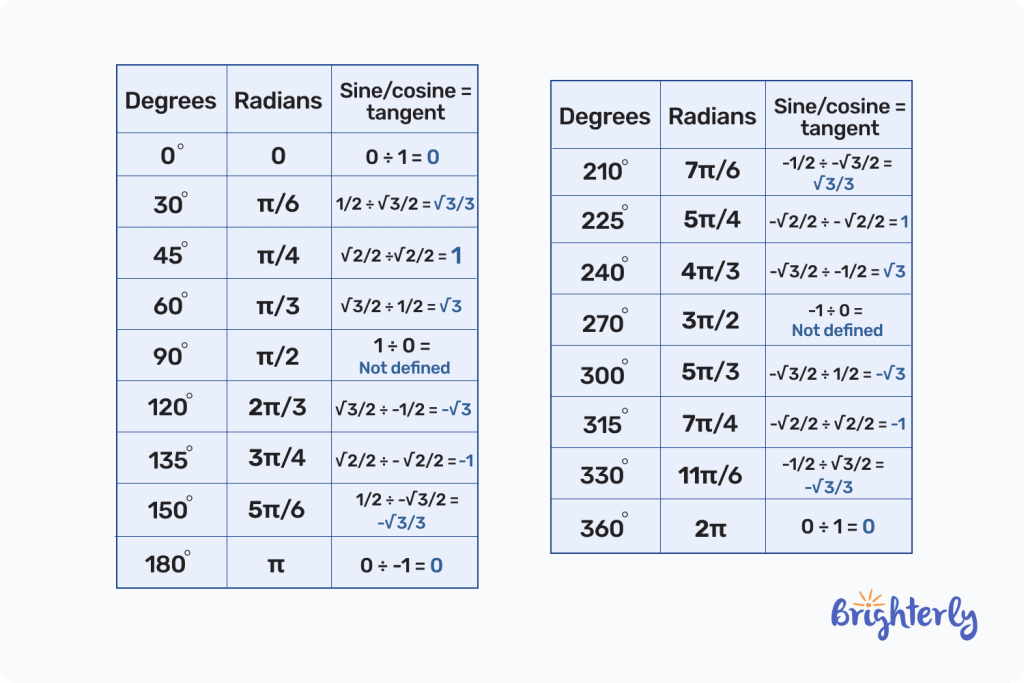
Therefore, the unit circle with tan in a tabular form is:
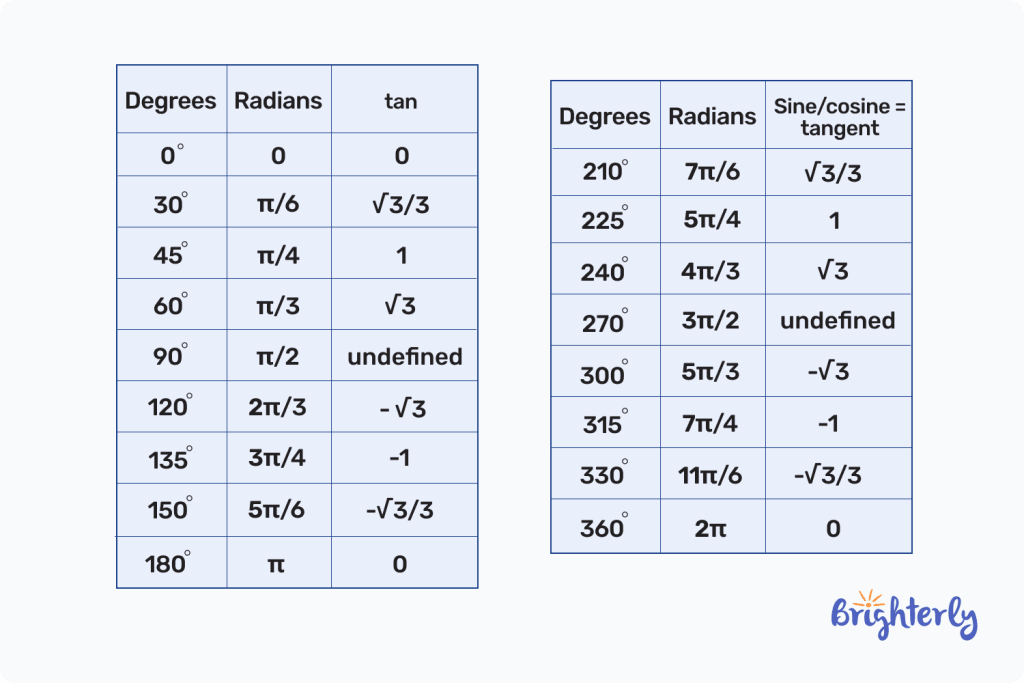
However, when the unit circle with a tangent chart is in a circle, here’s how it looks:
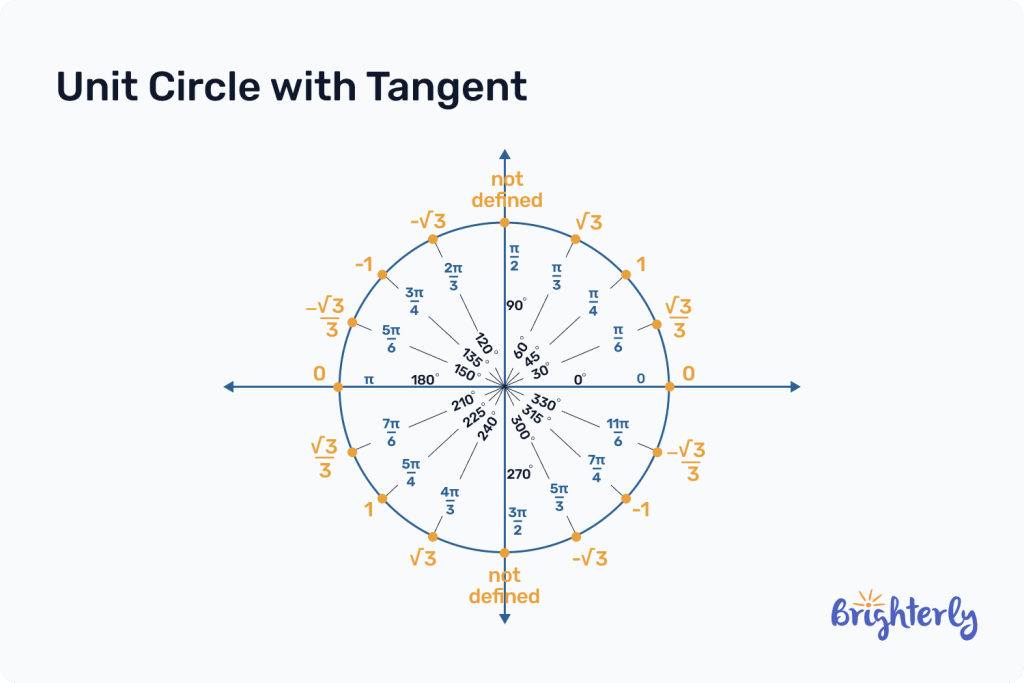
Thus, we can interpret the filled out unit circle with tangent as follows: when the angle is 120° or the radian is 2π/r, the corresponding tangent is -√3. Likewise, if the angle is at 90° or the radian is π/2, the tangent will be undefined, and so on.
This unit circle chart also helps us identify that the unit circle with values can be divided into four quadrants:
- The first quadrant contains the angles 0 to 90 degrees (0 to π/2 radians) and all the unit circle values are positive, i.e., sine, cosine, and tangent.
- The second quadrant contains the angles from 90 to 180 degrees (π/2 to π radians). Here sine is positive and cosine is negative, making tangent negative.
- The third quadrant contains angles 180 to 270 degrees (π to 3π/2 radians). All the values are negative.
- The fourth quadrant contains angles 270 to 360 degrees (3π/2 to 2π radians).
Note that the tangent is undefined at 90° (π/2) and 270° (3π/2) because the cosine value in both instances is 0 (in math, anything divided by 0 is undefined). Remember that tangent is sin/cos and in these cases, the coordinates of the circle are (0,1) for 90° (π/2) and (0, –1) for 270° (3π/2).
Equations of the Unit Circle and Tangent
The equations below are the individual formulas for calculating the unit circle and the tangent respectively.
Writing Equations of the Unit Circle
Derived from the Pythagoras theorem, the unit circle equation: x² + y² = 1, is used to find the points (x and y- coordinates) that are a unit away from the center of the circle.
Writing Equations of Tangent
The tangent equation is tan(θ) = sin(θ) / cos(θ). Remember that the sine is the y-coordinate and the cosine is the x-coordinate for the unit circle. This is because the point of the circle is expressed in (x, y).
Practice Problems on the Unit Circle and Tangent
Solved Math problems 1
Which of the following is true of the location of an angle that is 45°, and whose tangent value is 1?
- It is located in the first quadrant
- It is located in the second quadrant
- It is located in the third quadrant
- It is located in the fourth quadrant
Solution
| It is located in the first quadrant. |
Unit circle with tangent: practice math problems
Frequently Asked Questions on the Unit Circle and Tangent
Why is the unit circle important in trigonometry?
The unit circle is important in trigonometry because it educates learners on trigonometric functions (sin, cos, and tan), It also helps learners identify the exact points of a circle that corresponds to an angle.
Where is tangent undefined on the unit circle?
Tangent is undefined at 90 degrees(π/2 radians) and 270 degrees (3π/2 radians) in the filled-in unit circle because the cosine (the x-coordinate) is 0.
How is the tangent related to the unit circle?
The tangent is related to the unit circle because it explains the relationship between the length of a line and the angle formed when it intersects with the circle at a right angle.
Homework help with math tutor [grade 1-8]
Help your child achieve their full math potential
Choose kid's grade
Math homework help for grade 1-8
Join Brighterly and boost your child's math skills with our best tutors.
