• Learning Platform
• /
• Knowledge Base
• /
• X Squared – Definition, Examples, Facts

X Squared – Definition, Examples, Facts

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on April 7, 2026

X squared, or the concept of squared in general, is fundamental in math. X square essentially means multiplying the number by itself. It’s a topic your child will use throughout their math journey constantly.

Read on to learn what x squared is, what does x squared equal to, how to calculate it, and how not to confuse x squared with 2x.

What Is X Squared?

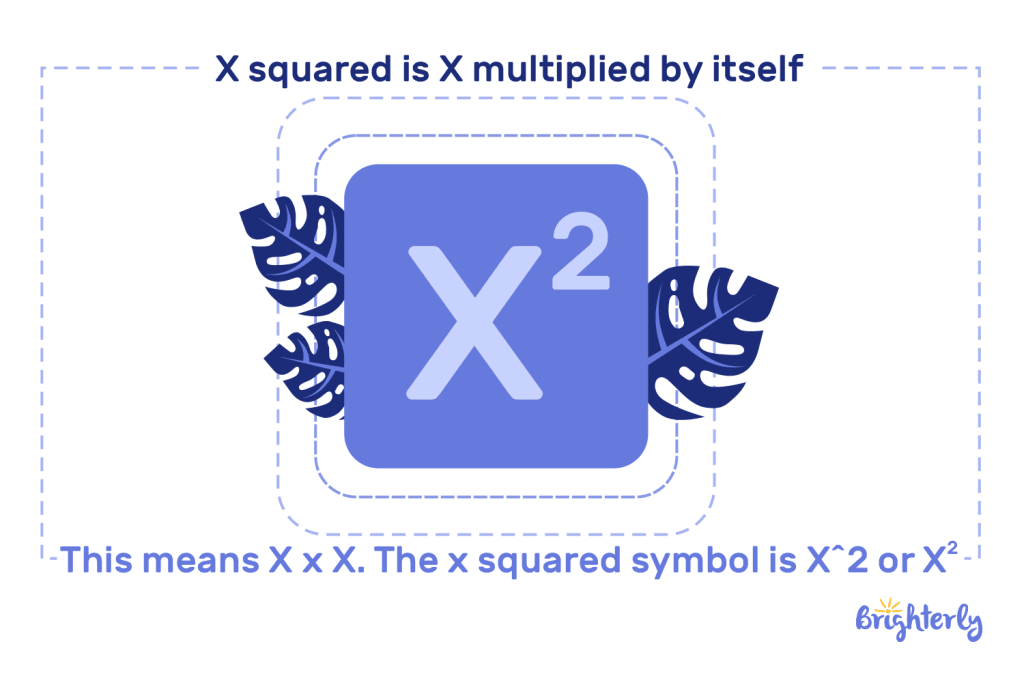
X squared is X multiplied by itself. This means X × X. The x-squared symbol is X^2. 

In this equation, 2 is an exponent of X.  Therefore, if X were multiplied by itself 3 times, the exponent would be 3 and expressed as X^3. 

Likewise, x squared times x squared will be X^4.

However, let’s focus on X squared for now.

Definition Of X Squared

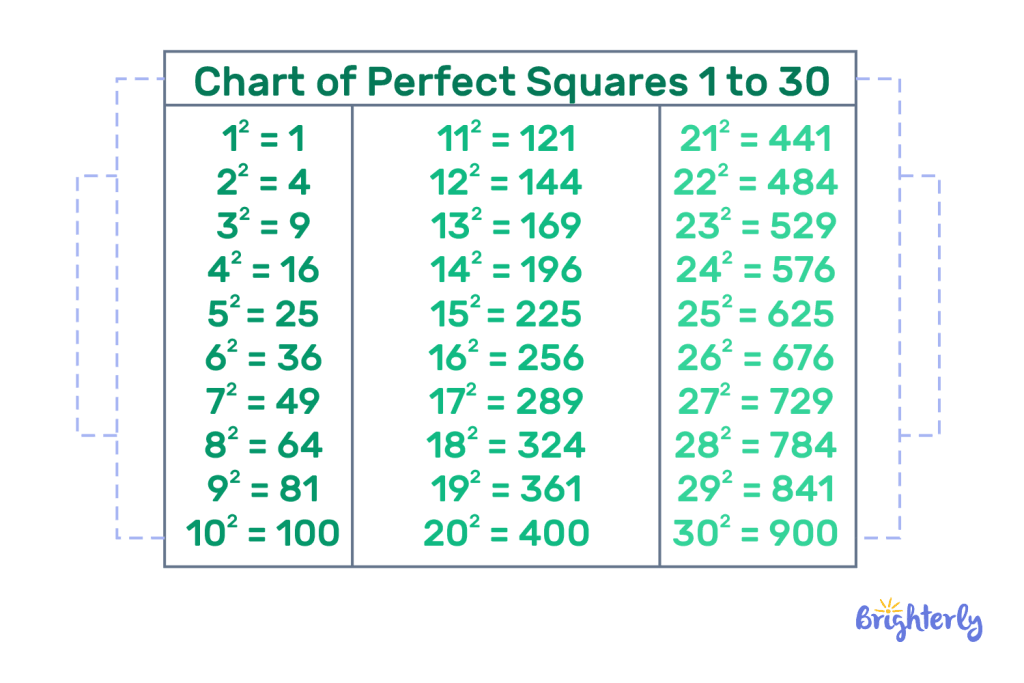
X squared definition is the multiple of a number or variable by itself. For example, if X is 4, then X squared (X^2) is 42 or 4 × 4, which equals 16.

Therefore the x^2 formula is X × X.

Examples Of X Squared

Squaring numbers can be straightforward, as with whole numbers, but they can also get quite technical. Let’s look at some examples below:

Understanding X Squared

We have established that X squared (expressed as X2) is the multiplication of a number by itself. Let’s go over some other mathematical statements to understand this concept more:

• X squared times X (x^2 times x): This is X^2 × X = X3. For instance if X = 2, then 2^2 × 2 = 2^3 or 2 × 2 × 2 = 8.
• x times x^2 ( x*x^2) or x(x^2): x times x squared is the same as X squared times X.
• X squared plus X squared: We express this as X^2 + X^2 = 2X^2. If X was 6, then 62 + 62 = 122
• x squared divided by x: This is X^2 ÷ X = X. If X is 4, then 42 ÷ 4 = 4
• X divided by X squared (x/x^2): X ÷ X^2 = 1/x. If X = 6, then 6 ÷ 62  = ⅙
• The square root of X^2: It is a known mathematical rule that the square root of a squared number is that number. Thus, √X^2 = | X |. If X is 144, then √144^2 = 144.

The Importance Of X Squared In Mathematics

The concept of X squared depicts the squaring of mathematical variables, and this plays an important role in mathematics because it occurs in various mathematical fields such as geometry, algebra, and graphs, as well as in science and real-world usage.

The Role Of X Squared In Algebra

We come across X squared in algebra when solving quadratic equations, factoring, expanding expressions, and so on. Its primary role is to help understand squared relationships, solve quadratic equations, and accurately model graphs, especially parabolas.

Properties Of X Squared

Unique Characteristics Of X Squared

The square of a number is always non-negative (positive or zero) even if the number is negative. This is because the product of two negative numbers is always positive. 

The only time the square of a number can be 0 is if the number itself is 0.

Common Behaviors And Patterns Of X Squared

In a parabola graph where y = X^2, y is positive if X is less than or greater than 0. However if X = 0, then y = 0 because 0^2 = 0

Math program

Help your child reach their full potential!

Answer a few quick questions about your child’s learning, and we’ll recommend next steps.

Take the quiz

How To Find The Value Of X²?

Finding the value of x square is quite simple if you already know the value of x. Squaring the number, or raising it to the power of 2, is essentially multiplying the number by itself. So, what you need to do to calculate x squared is simply x times x. Calculate the outcome, and you’ll have your value. For example, 

5 squared = 5 x 5 = 25

7 squared = 7 x 7 = 49

For single-digit numbers, knowing the times tables can make calculating the x-squared value even easier, as you already know them.

Difference Between X And X Squared

Is X Squared The Same As 2x?

One common point of confusion for many people is x squared vs 2x. It’s very important to remember that the square of x and x times two are two different mathematical operations, and produce different results for most numbers. The fundamental difference is that by squaring x, you multiply the number by itself (x times x), while in the case of 2x, you multiply x by 2.

Comparative Analysis: Linear Versus Quadratic

In a graph where X is a straight line, such as y =mx + b, it is known as a linear function. 

However, X^2  creates a curved “U” shape known as a parabola, such as y = ax^2 + bx + c.

The X^2 represents a quadratic function and X a linear function. Knowing the difference is important in solving algebraic and calculus problems.

Impact Of Squaring On Function Behavior

By squaring a variable, we change its function. In a graph, it changes X from a linear function to X^2, a quadratic function.

Equations Involving X Squared

Here are some simple and complex equations involving X-squared.

Simple Equations Involving X Squared

X squared can apply to whole numbers, whether positive or negative, and all we have to do is multiply it by itself, such as:

92 = 9 × 9 = 81 

–62  = –6 × –6 = 36

Complex Equations Involving X Squared

X squared can also appear in complex equations such as 2x^2 –5x + 2 = 0. Let’s look at the solution.

Writing Equations With X Squared

To solve the equations properly, you need to use the quadratic formula.

The standard form of quadratic equations is ax^2 + bx + c = 0, and the quadratic formula is:

X = –b ± √b^2 − 4ac/ 2a

We can therefore solve the equation 2x^2 –5x + 2 = 0 through the following steps:

Step 1: Find the values for a, b, and c: a = 2, b = –5, and c =2

Step 2: Put the values into the quadratic formula: x = –(–5) ± √(–5)2 – 4 (2) (2) /2 × 2

Step 3: Simplify: x = 5 ± √25 – 16 / 4

X = 5 ± √9 / 4

X = 5 ± 3 / 4

X = 5 + 3 / 4 = 8 / 4 = 2 

OR

X = 5 – 3 / 4 = 2/4 = ½

Therefore, X = 2 or X = ½.

Guidelines For Writing Quadratic Equations

With the following guidelines, let’s convert a non-quadratic equation to a quadratic equation. Our non-quadratic equation is 8×2 + 4 = 3x.

• a must not be equal to 0. In the equation given, a is 8. 
• Arrange all the terms in descending order of degree. x squared is always the greatest, i.e., x^2, x, then a constant. Our constant here is 4. So the equation is arranged as 8×2 – 3x + 4. Because we moved 3x to the opposite side of the equal sign, it becomes negative.
• The equation should be equal to 0: 8×2 – 3x + 4 = 0

Other guidelines include:

• If fractions are present, simplify the equation first.
• There should be no value greater than x squared (x^2).

Solved Examples

Easy Level Practice Problems

Solved Math Problem 1

Solve the following:

• If x squared  = 81, what is the value of x?
•  X = 11, what is X2.?

Solution

 Intermediate Level Practice Problems

Solved Math Problem 2

Solve the following:

• What Is X2 , when X = –9 + 13

Solution

First, we solve the equation for X:

–9 + 13 = 4

Hard Level Practice Problems

Solved Math Problem 3

Find the value of X in decimal for the following equation:

• 3×2 – 9x + 3 = 0.

Solution

We solve this using the quadratic formula which is :

X = –b ± √b2 − 4ac/ 2a

a = 3

b = –9

c = 3

Now, we substitute the values in the formula:

X = –(–9) ± √–92  − 4 × 3 × 3 / 2 × 3

X = 9 ± √81 – 36/ 6

X = 9 ± √45/ 6

X = 9 ± 6.70/ 6

X = 9 + 6.70/ 6 = 15.70/ 6 = 2.61

OR

X = 9 – 6.70/6 = 2.3/6 = 0.38.

Practice Problems on X Squared

X Squared Worksheets

In this article, we looked into what X^2 is equal to when it is added, multiplied, or divided by other values. To understand more about the square symbol in math, we recommend that you check out our free worksheets:

• Factoring quadratics worksheets 
• Solving quadratic equations by factoring worksheets 
• Factoring by grouping worksheets 

Frequently Asked Questions On X Squared

Why Is X Squared Important In Mathematics?

Square of X is important in mathematics because it occurs in various mathematical fields such as geometry, algebra, and graphs. Likewise, it is applicable in science and real-world usage.

How Does X Squared Behave In An Equation?

X squared is always non-negative, even if the number is negative. Also, in a quadratic equation, X^2 tells us the shape of the graph.

What Is The Difference Between X And X Squared?

X refers to a single variable. It can be used to represent a number. X squared refers to the product of that number by itself. For example, X may be 2, and X^2 is 2 × 2, which gives us 4.

Can X Squared Be Negative?

No. Since X squared is a number multiplied by itself, it cannot be negative. This is because even if X is negative, negative multiplied by negative is positive.

Why Is X Squared Written As X²?

We write the expression X squared for convenience. While the efficiency is not that notable in x squared symbol itself, as we only do one multiplication, it is noticeable when raising numbers to a larger power. For example, instead of writing 2×2×2×2×2, we simply write 2^5.

Jessica Kaminski

92 articles

Jessica is a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.