• Math tutors
• /
• Knowledge Base
• /
• Addend in Math

Addend in Math

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on December 21, 2024

Addends in math are the numbers in an addition equation that make up the sum. 

Here, we discuss addend meaning as well as addends example, practice problems, and worksheets. 

Keep reading!

What is an addend in math?

Addends are the components that make up a sum. Addition is an arithmetic operation that has to do with putting together two or more numbers, variables, quantities, or values to create a new number known as the sum.

Per the addends definition, addends are the numbers, variables, quantities, or values that are combined in an addition equation.

Here’s how we may use addend in a sentence: If Jace picked 7 tulips and 3 roses, he has picked a total sum of 10 flowers. If expressed this will be 7 + 3 = 10.

In this equation, 7 tulips and 3 roses are the addends and sum is the total flowers (10).

Addend Definition

We may define addend as the numbers in an addition equation that form the sum. For example, in the addition equation: 5 + 5 = 10, 5 and 5 are the addends.

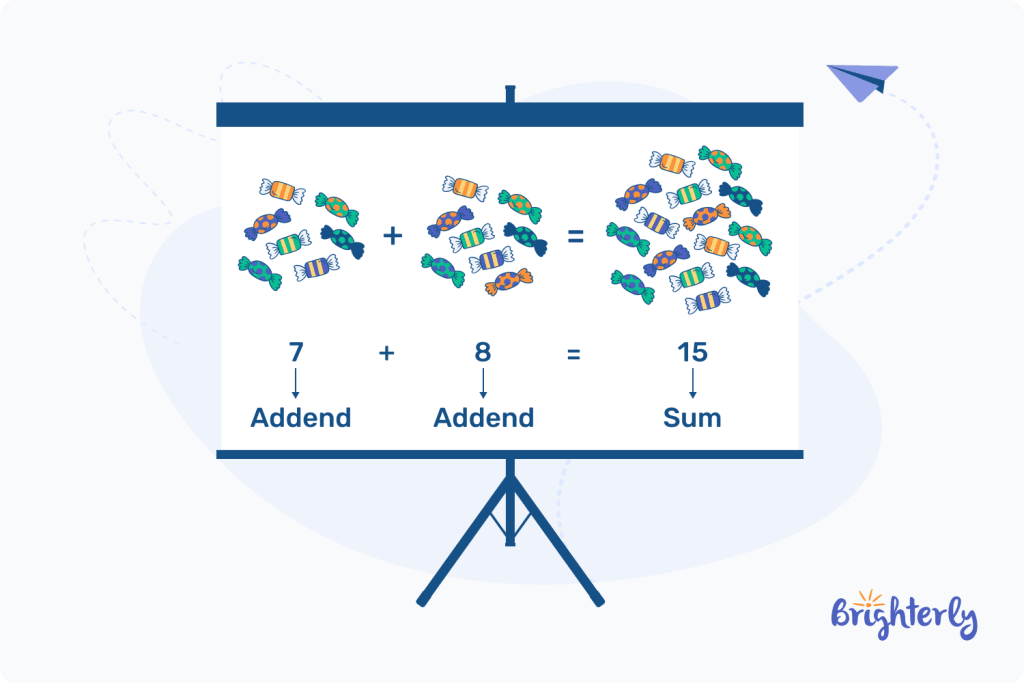
Two addends that are the same number are called identical addends and the process of adding them is called doubling. 

Different Forms of Addends

Addends are not just positive whole numbers. They may appear as negative whole numbers, fractions, decimals, terms, or even complex equations. 

• Positive numbers: This is the most common form of addends where the numbers in the equation are positive integers such as 1, 2, 3, 4, etc.
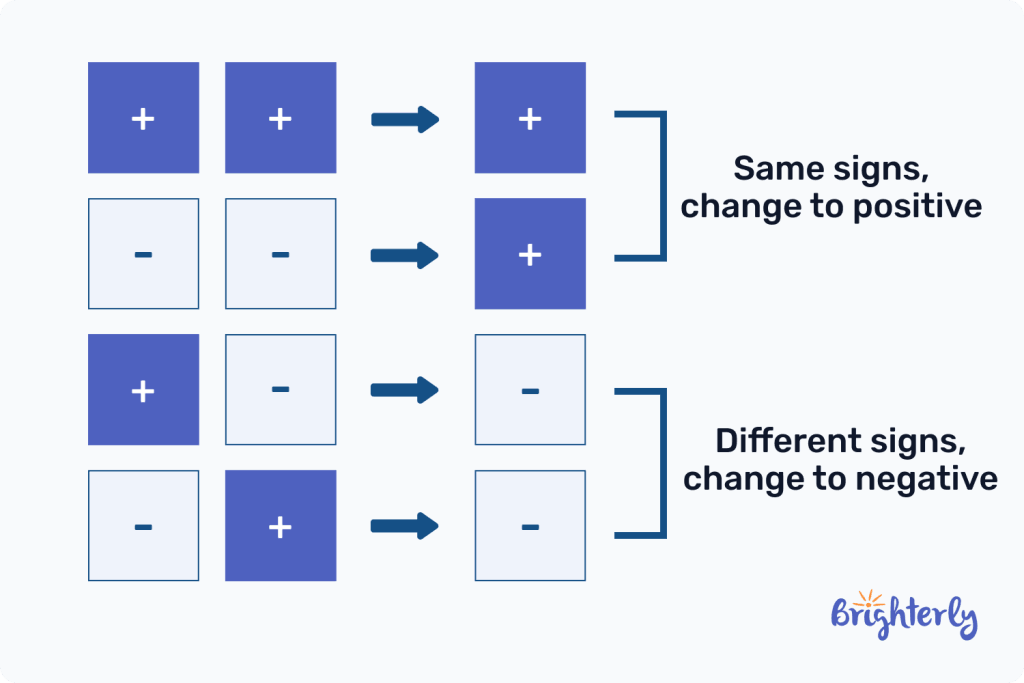
• Negative numbers: Here, the numbers we add are negative integers such as –1, –2, –3, –4, etc. When we add a negative number to another negative number the sum is negative.

• Decimals: We can put together decimal numbers to form a sum. The method of calculation is the same as adding positive integers, except, we also have to watch out for the decimal point.

• Fractions: Math addends can also be in the form of fractions. When this happens, if the fractions share the same denominator, we add the numerators to get the sum and leave the denominator as is. However, if the denominators are different, we find their lowest common multiple, change the numerators to match the new denominator, and then add just the numerator.

• Terms: Unknown values can also be addends. This can be variables such as x and y.
• Complex equations: Addends can also be comprised of more than one of the forms we listed above. This means we can have a positive number, decimal number and terms as addends.

The components of an addition equation separated by the plus sign (+) are the addends.

Examples of addends

Let’s go over the examples of addends.

Positive numbers

• 15 + 5 = 20. The addends are 15 and 5.

Negative numbers

• –12 + –7 = –19. –12 and –7 are the addends.

Decimal numbers

• 2.4 + 5.8 = 8.2. 

Fractions

• ½ + ½ = 1

Terms

• x + x = 2x

Complex equations: 

• 2x + 0.5 + 3x = 5x + 0.5

Math tutors

Is your child bored with math?

Our interactive lessons will engage them from the first class

Let’s start learning Math!

Rule of Change of Addends

The rule of change of addends is the addition principle which states that whenever we increase or decrease the addends by a particular amount, the sum also increases or decreases by that amount.

For instance, in the addend example, 12 + 9 = 21, reducing 12 by 2 makes the equation become 10 + 9 = 19.

We can see that the sum, 21 is also reduced by 2 to become 19.

Likewise, if we increase one of the addends (9) by a number (2), the sum increases by 2.

12 + 11 = 23.

Solved Examples on Addend

Solved Math problem 1

Give examples of sums with one addend of 10.

Solution

Here are some addend examples that include 10:

Solved Math problem 2

What are the addends in the following equations:

•  53 + 42 + 1 = 96
• 22 + 11 = 33
• 3x + 4x = 7x
• –2 + 2 = 0

Solution

Practice Problems on Addend

Frequently Asked Questions on Addend

What are addends?

Addends are components of an addition equation that make up the sum. The addends are separated by the plus sign (+).

How can I help my child understand addends better?

Help your child understand addends by using real-life objects to demonstrate how much they are when counted together. For instance, you can give them 2 cookies first, then 3 cookies, and ask them to count how many cookies they have in total. Also, use interactive games and online resources like the ones available at Brighterly.

What are some strategies for teaching addition and addends?

Some strategies that can make addition and addends easier include using a number line to add by counting rightwards from the first addend to where you land — you move towards the right as many times as the number of the second addend. Another strategy is to break down the number into smaller parts. For instance, when we want to add 4 + 7, we can break down 7 to 4 + 3 so the equation becomes 4 + 4 + 3 = 11. 

How can I make learning about addends fun and engaging?

Make learning about addends fun for children by using objects they play with and language they are familiar with. On paper, use interactive designs and attractive colors to maintain their attention. Brighterly’s worksheets are an excellent online resource for this.

What are some common misconceptions children may have about addends?

Some common misconceptions children may have about addends include thinking the addends must maintain the order given – the commutative property debunks this. Other misconceptions include thinking that addends must always be positive whole numbers. Zero cannot be an addend, and so on.

How can I assess my child’s understanding of addends?

You can know how much your child understands addition and addends by observing their comprehension skill in addition-related problems. Engage them in conversations and ask questions about addition and addends to see how well they understand the topic. You can also give them exercises such as in Brighterly’s worksheets to track their progress.

Addend: worksheets

In our worksheets you can find addend math examples for different levels including; addends example grade 1, addends example grade 2, and addends example grade 3.

Our worksheets are designed to match the respective grade level of your child.

• Addition on Number Line
• Addition with Regrouping
• Missing Addend Worksheets

Jessica Kaminski

72 articles

Jessica is a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.