Area and Perimeter – Definition with Examples
reviewed by Jo-ann Caballes
Updated on November 12, 2024
Shapes can have various forms of measurement. Here, we discuss area and perimeter, area vs perimeter, examples of area, practice questions, and more.
Happy learning!
What is area and perimeter?
Area and perimeter are two distinct measurements in geometry used for calculating the size and boundaries of shapes.
Area in math definition
The area is the amount of square space contained within a two-dimensional shape. We measure the area in square units, i.e. if it is a mile, we measure it in square miles, if it is in inches, we measure it in square inches, and so on
Perimeter definition in math
In a 2-dimensional shape, a perimeter is the total length that spans across the shape.
How to find the area and perimeter?
We can find the area for a 2-dimensional figure, through different formulas depending on the type of shape.
The perimeter is found by summing the lengths of all the sides of a polygon or a plane shape (square, triangle, rectangle, etc.).
Area and perimeter examples
Perimeter and area can prove useful in the conduct of our daily affairs from architecture, construction, farming, and many more. These are some area examples:
- We can measure the square feet of a wall by using area.
- With area, flat-screen TVs can be measured in square inches.
- Large landscapes can be measured in square meters with area too, and so on.
Perimeter too, can be applicable for real-life uses. Here are some perimeter examples:
- With perimeter, we can measure a fence around a house
- In scenes of construction, have you noticed yellow caution tape around the place? This perimeter outline is to secure the area where the construction takes place.
Differences between Area and Perimeter
Below are some differences between area and perimeter
| Area | Perimeter |
| Area is the measurement of the space a shape occupies | Perimeter is the measurement of the outside boundary of a shape |
| We measure area with square units | We measure the perimeter in linear units |
| The area is calculated in different ways depending on the type of shape. | Perimeter is the sum of the lengths of the sides of a polygon |
Area and perimeter formulas
Here are the formulas for area and perimeter of different shapes:
Square
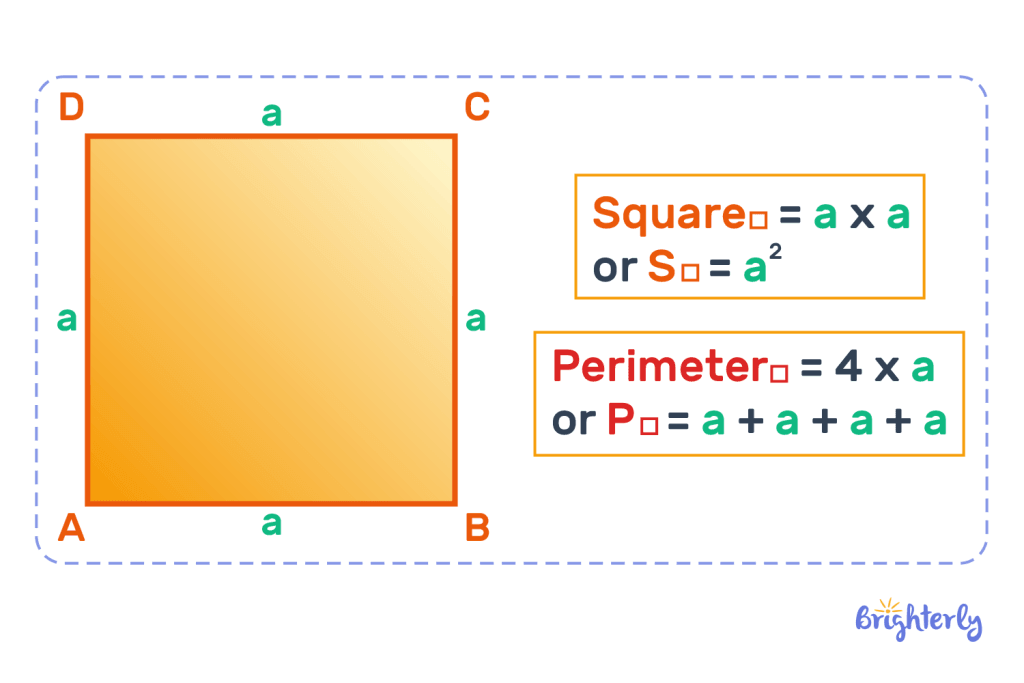
The perimeter and area of a square are:
The area for a square is the length multiplied by its breadth
Therefore, area = a × a or a2
The formula for the perimeter of the square is 4 multiplied by one side since all sides are equal or like we said earlier, you can add the sides:
Perimeter = 4 × a
OR
Perimeter = a + a + a + a
Triangle
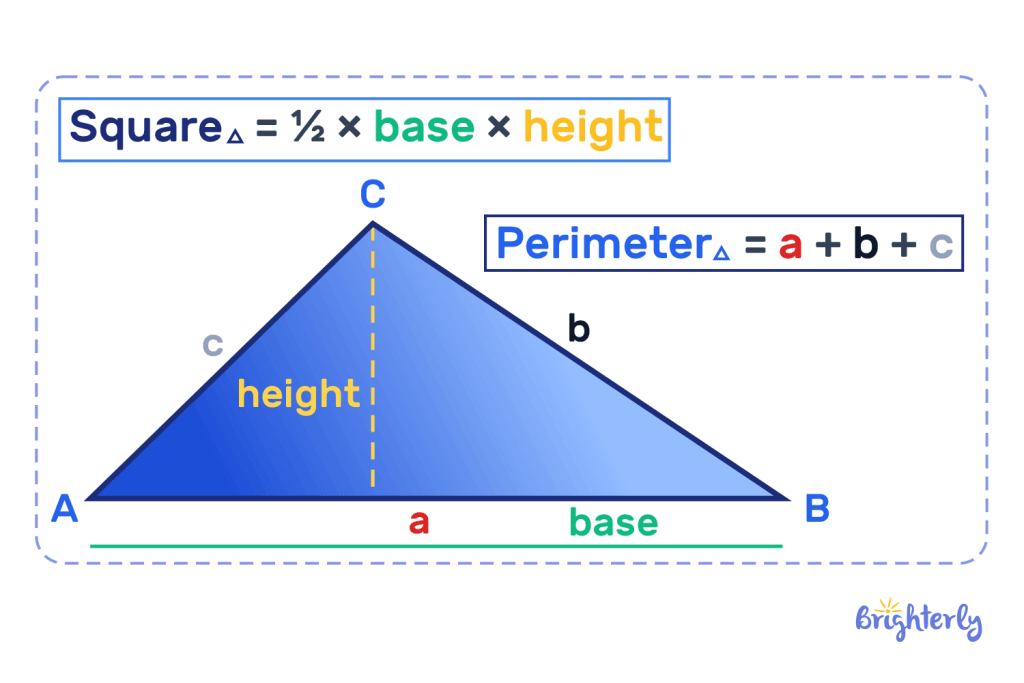
The area for a triangle is ½ multiplied by the base and by the height.
Area = ½ × base × height
The perimeter is the total summation of the sides.
Perimeter = a + b + c.
Rectangle
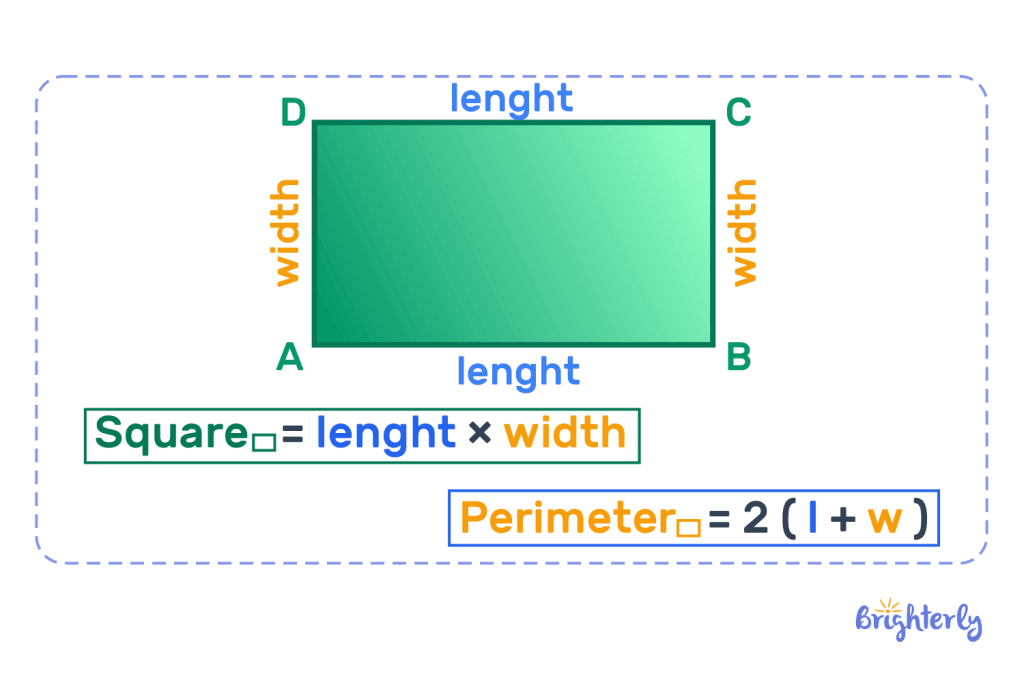
The area for the rectangle is the length multiplied by the width.
Area = length × width
The perimeter of the rectangle is 2 multiplied by the length plus the width since a rectangle has two equal sides.
Perimeter = 2(l + w)
Circle
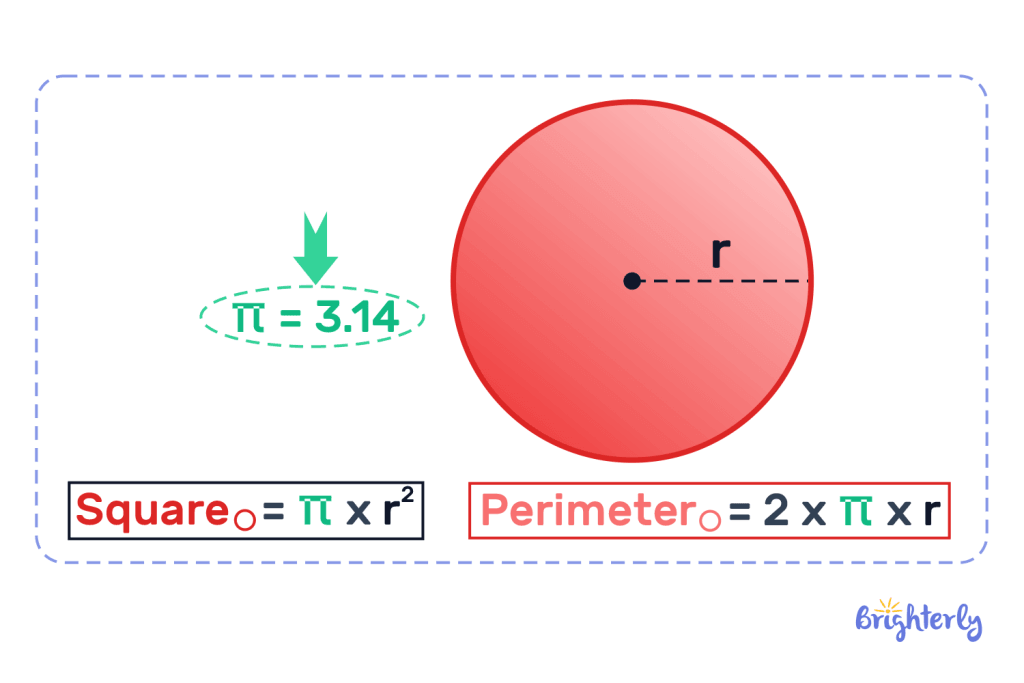
The area and perimeter of a circle are similar but not the same.
The area for a circle is pi multiplied by the square of a radius.
Area = π × r2
The perimeter of a circle is 2 multiplied by pi and the radius
Perimeter = 2 × π × r
Note that π = 3.14
Solved Math Tasks: Examples
Solved math problem 1
A square has an area of 42 square cm, what is the perimeter?
Answer
Following the formula for the area and perimeter of a square, we know that the area of a square is its length multiplied by its breadth, this means 42 cm2 = l × b.
The next step is to find the length for each side, to do this, we find the square root of 42 which is 6.48
|
Thus, perimeter = 4 × 6.48 =25.92 cm. |
Solved math problem 2
George has a triangular pizza slice with a base of 3 units and a height of 4 units, what is the area of the triangle?
Answer
We simply multiply ½ by 3 units and by 4 units to find the area:
½ × 3 × 4 = 6
|
The area is 6 square units. |
Solved math problem 3
What is the area of a circle when its radius is 10 cm?
Answer
Per the formula above, area = 3.14 × 10 × 10
|
Therefore, the area of the circle is 314 cm2. |
Area and Perimeter: Practice Math Problems
Area and Perimeter: worksheets
Although mainly used for 2-dimensional shapes, areas, and perimeter set the pace for understanding more complex measurements of shapes in geometry — hence why learning them is crucial for young mathematicians.
Practice more on area, perimeter, and other measurements with our free worksheets:
Math homework help for grade 1-8
Get the homework support your child needs!
Choose kid's grade
Math Program
Boost Your Child's Math Abilities! Ideal for 1st-8th Graders, Perfectly Synced with School Curriculum!
