Area of Triangle – Definition with Examples
Updated on January 12, 2024
The area of a triangle is a fundamental concept in geometry, representing the space enclosed by its three sides. This area is a two-dimensional measurement, typically calculated in square units like square centimeters or square meters. Understanding the area is crucial for various applications in mathematics, science, and engineering.
What is the Area of a Triangle?
The area of a triangle is a measure of the space enclosed within its three sides. To understand this concept, imagine a triangle drawn on a flat surface. The area is what you would measure if you wanted to cover the triangle completely with paint. This concept is fundamental in geometry and is often used in various mathematical calculations and real-world applications.
Area of a Triangle Formula
The most common formula for finding the area of a triangle is: Area = ½ × base × height. In this formula, the ‘base’ refers to any side of the triangle, and the ‘height’ is the perpendicular distance from the chosen base to the opposite vertex. It’s important to note that the height must be perpendicular to the base. This formula is versatile and can be used for all types of triangles, making it a fundamental tool in geometry.
Area of a Right Angled Triangle
Calculating the area of a right-angled triangle is straightforward using the standard area formula. In a right-angled triangle, one of the sides is perpendicular to another, forming a right angle (90 degrees). These two sides act as the base and height in the area formula. Therefore, the area of a right-angled triangle can be calculated by Area = ½ × base × height, where the base and height are the two sides that form the right angle.
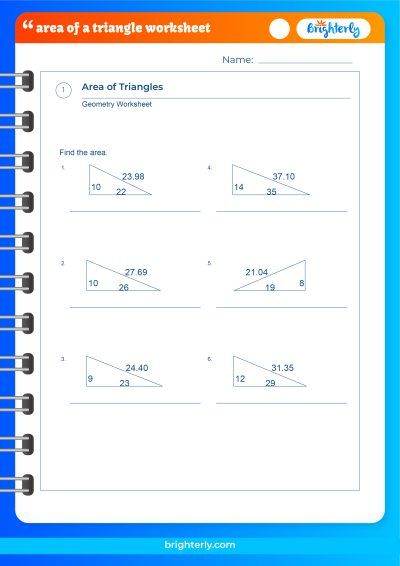
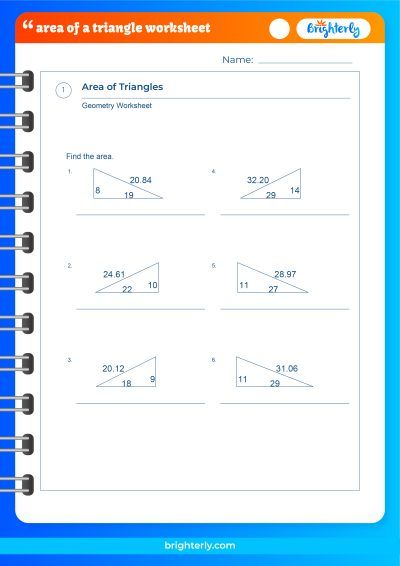
At Brighterly, we believe that practice is the key to mastery. That’s why we invite you to explore our area of a triangle worksheets, where you can find an array of additional practice questions, complete with answers.
Area of an Equilateral Triangle
An equilateral triangle has all three sides of equal length. To find its area, you can use the formula: Area = (sqrt(3)/4) × side². This formula derives from the standard area formula by substituting the height with the formula derived from the properties of an equilateral triangle. Since all sides are equal, using any side length will give the correct area.
Area of an Isosceles Triangle
In an isosceles triangle, two sides are of equal length. The area can be calculated using the standard formula, but finding the height might require additional steps. The height can be found by dividing the triangle into two right-angled triangles and then using the Pythagorean theorem. Once the height is known, apply the area formula: Area = ½ × base × height.
Area of Triangle Using Heron’s Formula
Heron’s formula is useful for finding the area of a triangle when all three sides are known. The formula is Area = sqrt(s × (s-a) × (s-b) × (s-c)), where ‘a‘, ‘b‘, and ‘c‘ are the lengths of the sides, and ‘s’ is the semi-perimeter of the triangle, calculated as s = (a + b + c) / 2. This formula is particularly helpful in cases where the height of the triangle is not readily available.
Area of Triangle With 2 Sides and Included Angle
When two sides of a triangle and the angle between them are known, the area can be calculated using the formula: Area = ½ × a × b × sin(C), where ‘a‘ and ‘b‘ are the lengths of the two sides, and ‘C‘ is the included angle. This formula is derived from trigonometric principles and is especially useful in trigonometry and physics.
How to Find the Area of a Triangle?
To find the area of a triangle, identify the type of triangle and the measurements provided. Use the standard area formula for most cases, but switch to specific formulas like Heron’s formula or the formula for the area with two sides and an included angle as needed. The key is to correctly identify the base and height or the applicable measurements and angles.
Area of Triangle when 3 Sides are Given
When the lengths of all three sides of a triangle are given, Heron’s formula is the most effective method to find the area. First, calculate the semi-perimeter (s), then apply the formula Area = sqrt(s × (s-a) × (s-b) × (s-c)). This method does not require the height of the triangle, making it particularly useful for irregular triangles where the height is not easily determined.
Practice Questions on Area of Triangle
Remember, the best way to learn mathematics is by applying the concepts in practical situations. Let’s walk through some practice problems that cover different types of triangles and the various ways we can calculate their areas.
-
Right-Angled Triangle
- Problem: The base of a right-angled triangle is 8 cm and its height is 5 cm. Find the area.
- Solution: Use the formula
A = 1/2bh(Area = 1/2 x base x height). Here, base (b) = 8 cm, and height (h) = 5 cm. So, the area of the triangle is 1/2 x 8 x 5 = 20 cm².
-
Equilateral Triangle
- Problem: Find the area of an equilateral triangle with a side length of 6 cm.
- Solution: Use the formula
A = (√3/4) * side². Here, side length = 6 cm. So, the area of the triangle is (√3/4) x 6² = 15.59 cm² (rounded to two decimal places).
-
Isosceles Triangle
- Problem: An isosceles triangle has a base of 10 cm and a height of 12 cm. Calculate the area.
- Solution: Use the formula
A = 1/2bh. Here, base (b) = 10 cm, and height (h) = 12 cm. So, the area of the triangle is 1/2 x 10 x 12 = 60 cm².
-
Triangle using Heron’s Formula
- Problem: Find the area of a triangle with sides of lengths 7 cm, 8 cm, and 9 cm.
- Solution: Use Heron’s formula
A = √[s(s - a)(s - b)(s - c)]. First calculate the semi-perimeter (s) = (7+8+9)/2 = 12 cm. Then, substitute these values into the formula to get: A = √[12(12 – 7)(12 – 8)(12 – 9)] = 26.83 cm² (rounded to two decimal places).
-
Triangle with 2 Sides and Included Angle
- Problem: Two sides of a triangle measure 5 cm and 6 cm, and the included angle is 60 degrees. What is the area of the triangle?
- Solution: Use the formula
A = 1/2ab sin(C). Here, a = 5 cm, b = 6 cm, and C = 60 degrees. So, the area of the triangle is 1/2 x 5 x 6 x sin(60) = 13.0 cm² (rounded to one decimal place).
Frequently Asked Questions on Area of a Triangle
We’ve gathered some of the most common questions we receive about the area of a triangle, and have provided comprehensive answers to ensure your understanding is as solid as a well-built triangle.
Can the area of a triangle be negative?
- No, the area of a triangle cannot be negative. Area represents a physical space and is always a positive value.
Is the formula for the area of a triangle always ½ × base × height?
- While ½ × base × height is the most common formula, other formulas like Heron’s formula or the formula for two sides and an included angle are also used, depending on the information available.
How do you find the height of a triangle?
- The height can be found using geometric methods, such as drawing a perpendicular from a vertex to the opposite side, or using trigonometric functions in more complex triangles.
Can Heron’s formula be used for all types of triangles?
- Yes, Heron’s formula can be applied to any triangle as long as the lengths of all three sides are known.
Information Sources:
Online Winter Math Camp for Grades 1-8
Join us to help your kid achieve their full math potential.
Choose kid's grade
Online Winter Math Camp for Grades 1-8
Join our Math Winter Camp and boost your child's math skills with our best tutors.
