Brackets in Math – Definition with Examples
reviewed by Jo-ann Caballes
Updated on July 15, 2025
Most people are familiar with brackets in the English language. But, it also applies to mathematics.
And just like in English where we use brackets to group words and phrases, we may also use brackets in math to group expressions and numbers.
Additionally, brackets are the first order of operation for solving mathematical problems. Let’s learn more about the brackets in math meaning and brackets examples in this article.
What are Brackets?
Math brackets are symbols used to group numbers and mathematical expressions together, giving these grouped numbers or expressions higher priority over other operations in the equation.
What does a bracket look like?
When we picture a bracket in math, we probably think of the round, symmetrical curves “( )”. These are called parentheses or round brackets and are only one of the different types of brackets.
However, there are other types.
What Are the Different Types of Brackets?
There are three main types of brackets in math. Here they are and the corresponding brackets symbol:
- Round brackets or Parentheses: “( )”
- Curly brackets or Brace brackets: “{ }’.
- Square brackets, also known as Box brackets: “[ ]”
Did you notice the difference between these bracket symbols? Well, they also serve different purposes.
Let’s go over them.
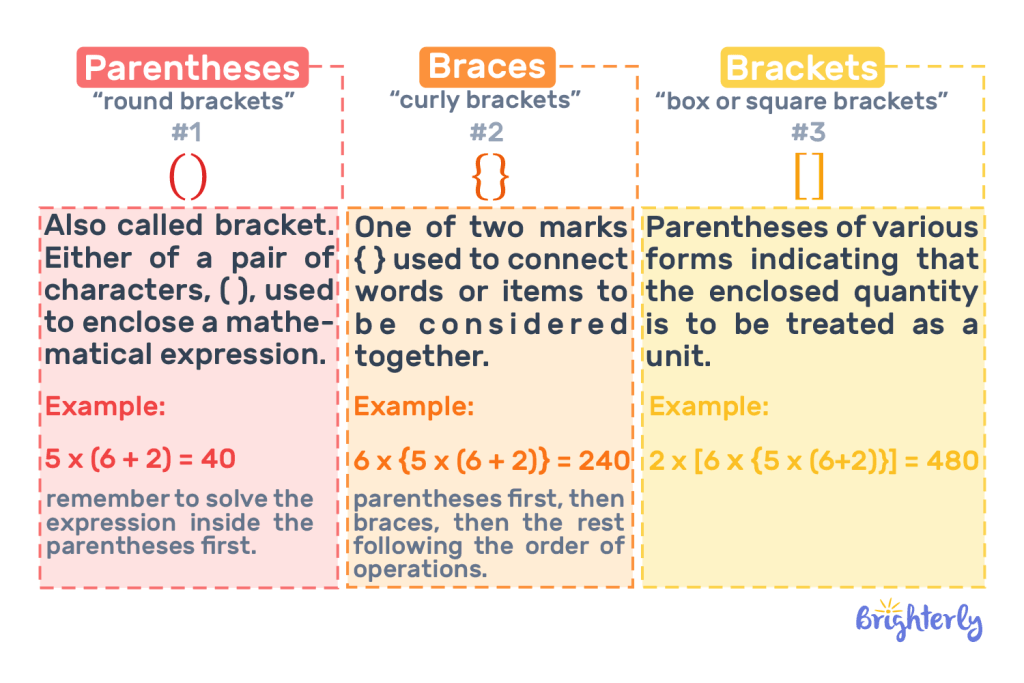
What Are Parentheses Brackets?
Parentheses or round brackets “( )’ are the most common types of brackets used in math. The other types of brackets are sometimes even called types of parentheses but parentheses are a type of bracket.
We use the parentheses bracket symbol to group expressions within an equation. Parentheses are also the first order of operations according to PEMDAS or BODMAS, which means we always solve the numbers in the parentheses first in an equation.
Parentheses in math example
For example, in the equation 3 + (4 – 1) we first solve the number in the parentheses, i.e., 4 – 1 = 3. Then, we can solve the equation outside: 3 + 3 = 6.
What is the difference between brackets and parentheses in math?
Parentheses are one of the different types of brackets, round brackets to be specific. Square and curly brackets are some of the other brackets in math that serve unique functions different from parentheses.
How to Use Parentheses in Math?
Aside from grouping numbers in equations, parentheses perform other functions, and here are some of them:
We use parentheses for multiplication:
When there is no arithmetic operation between a number and the number(s) inside parentheses, the parentheses serve a multiplication purpose.
For example, to solve the equation 4(5) the parentheses bracket symbol would be converted to multiplication, which means it becomes 4 × 5, which equals 20.
Another example is 6 (7 – 3)). Here, we’d first solve the numbers in the parentheses, 7– 3 = 4. Then multiply by the number outside the parentheses, 6 × 3 = 18.
We use parentheses to isolate numbers
Parentheses help in isolating numbers that are unique to the original equation.
For example, in an addition equation, parentheses can help us identify negative numbers by isolating them:
9 + (–6) + 4 + 2.
We use parentheses to group numbers
This is the primary use for parentheses bracket in math— to group numbers. This is also the first order of operation in solving mathematical equations, i.e., solving the grouped numbers before the rest.
For example, 34 + 21 (4 – 2).
Here, we solve the equation within the parentheses (4 – 2) = (2). Then, we use the parentheses as multiplication so the equation becomes 34 + 42 = 76.
What Are Curly Brackets?
Also known as brace brackets or simply braces in math, the curly brackets are used to group a set in mathematics. For instance, to express numbers 1 – 5 in a set, it would be:
{1, 2, 3, 4, 5}
Since it is a type of bracket, the curly brackets symbol is also used to group numbers. However, this applies only to large equations where there is already a parenthesis. The braces symbol comes after the parentheses but before the square brackets. For instance:
[9 – {4 + (–3)}] + [6 + {3 × (–2)}]
We’d solve this as follows:
[9 –1] + [6 +(–6)]
8 + 0
= 8.
Other instances of where we may use the curly brackets in math are:
7[8 + {9 – 4 (5)}], [12 – {4 × (5 + 7)}], etc.
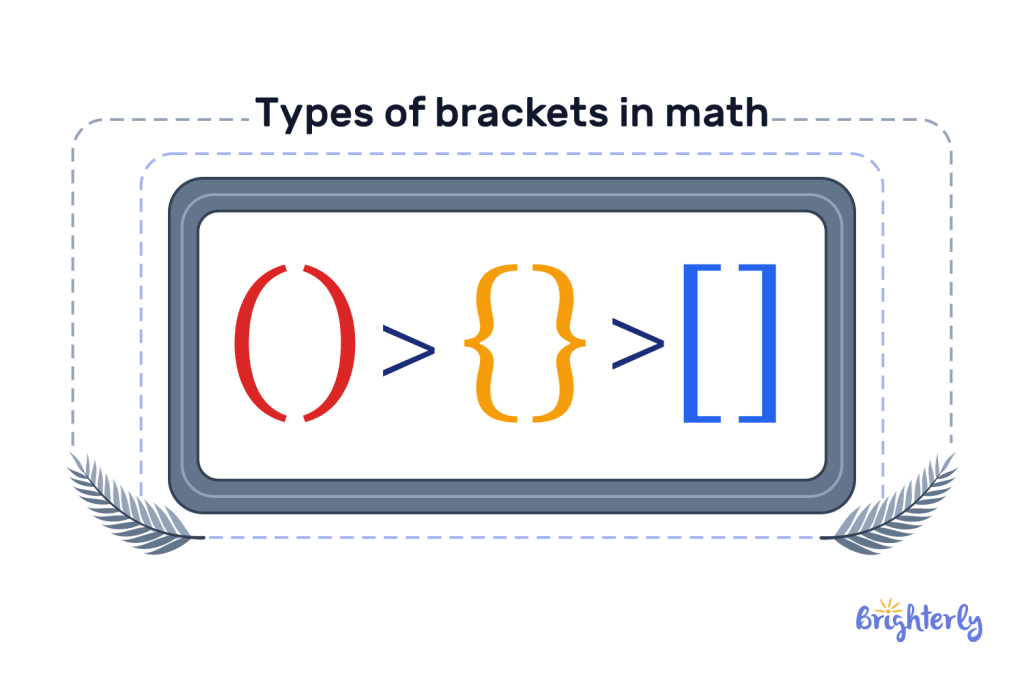
The order for using the curly brackets with the other brackets is:
What Are Square Brackets?
Square brackets are the more encompassing type of bracket. In large and complicated equations, a square bracket can group sub-equations into one equation. This way, the equation is kept clear.
For instance:
[32 × (6 + 7 – 12) + (–8 + 5)]
The square brackets help us maintain control of the equation, allowing us to solve each sub-equation, especially when multiple groupings are involved.
Parentheses vs brackets in math
Some people often confuse all the different types of brackets as parentheses. So, let’s look at brackets vs parentheses in math to see their differences.
What Is the Order of Operations for Brackets?
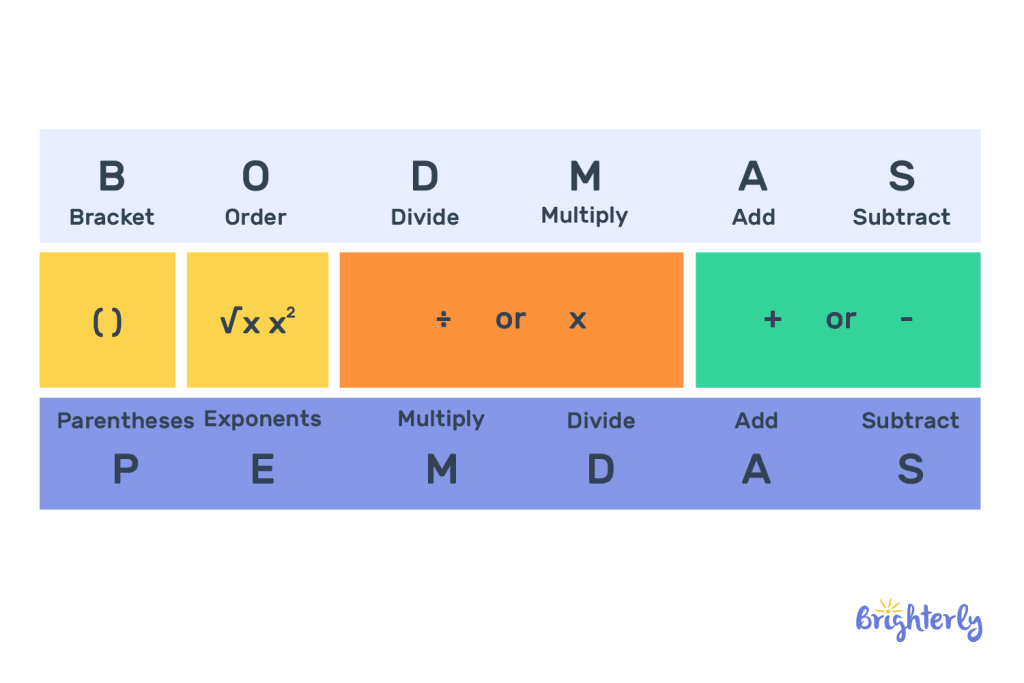
The order of operations is a set of guidelines to be followed when solving any mathematical equation.
You can remember it by the acronym PEMDAS or BODMAS.
Let’s look at an example of PEMDAS in action:
For the equation; 21 – 45 × 7 – 9 × 0, if we solve it directly, it would be:
= –24 × 7 – 9 × 0
= –168 – 9 × 0
= –177 × 0
= 0.
This is incorrect. However, if we solve the problem with the PEMDAS order it becomes:
Multiplication first:
21 – 315 – 0
Then subtraction:
–294.
Thus, the correct answer is –294.
According to these rules, we always solve brackets or parentheses first. But what happens when there is more than one type of bracket in an equation?
As we mentioned earlier, we solve the parentheses or round brackets first, then the curly brackets, and finally, the square brackets:
[{()}]
This means we follow the order of operations in the parentheses first before the braces and we solve the box bracket last.
For example:
5 [7 + {–3 + 4(6 + 1)}]
5 [7 + {–3 + 4(7)}]
5 [7 + {–3 + 28}]
5 [7 + {25}]
5 [32]
= 160.
In this example, we solved the operations within the round bracket before proceeding to the curved bracket, and then the square bracket.
Please note that per the brackets in math-s rules, the order of operations should be followed within the bracket types, meaning exponents come before multiplication or division which comes before addition or subtraction.
Solved Examples on Brackets
Solved math problem 1
What is the solution to the equation:
(56 – 14) – (12 + 8)
Solution
According to the BODMAS rule, we first solve the contents of each bracket, so the equation becomes:
| (42) – (20) = 22. |
Solved math problem 2
Following the rules to solve equations in bracket math, answer the following:
[8 × (4 + 9 – 12) + (8 × 0)]
Solution
First, we solve the parentheses; (4 + 8 – 12) + (8 × 0)
= (0) +(0)
Then, we can solve the square brackets;
[8 × (0))]
| Therefore, the result is 0. |
Solved math problem 3
What is the solution to the equation:
(22 ÷ 4 + 3 × 2) – (64 ÷ 3 – 12)
Solution
Even when solving inside a bracket in math, remember that multiplication or division comes before addition and subtraction. Therefore, we solve it as follows:
(5.5 + 6) – (21.33 – 12)
(11.5) – (9.33)
| = 2.17 |
Solved math problem 4
Use the rules for brackets in math to solve the following:
{(9 + 3) ÷ (8 – 3)} × 3
Solution
First, we start with the parentheses:
{(12) ÷ (5)} × 3
Then, the curly brackets:
{2.4} × 3
| = 7.2 |
Solved math problem 5
Solve the equation according to the bracket types:
[316 – {(9 ÷ 3) – (7 – 4) + 5} + 20]
Solution
First, we solve the contents in the round brackets:
(9 ÷ 3) = 3
(7 – 4) = 3.
Our equation thus becomes:
[316 – {(3) – (3) + 5} + 20]
Then, we solve the curly brackets:
{0 + 5} = 5.
Finally, we solve the square brackets:
[316 – {5} + 20]
| [311 + 20] = 331 |
Solved math problem 6
9 × [4 + {17 – (14 – 5)}]
Solution
Again, we start with the parentheses:
(14 – 5) = 9.
Then, the curly brackets
{17 – (9)} = 8
And the square brackets:
[4 + {8}] = 12
Finally, we solve what is outside the brackets:
9 × [12] = 108.
| The solution is 108. |
Solved math problem 7
Following the rules to solve equations in bracket math, answer the following:
16 {(30 ÷ 15) + (72 ÷ 8)} – {(28 ÷ 7) + (14 ÷ 2)}
Solution
16 {(2) + (9)} – {(4) + (7)}
16 {11} – 11}
| 176 – 11 = 165. |
Practice Problems on Brackets
Frequently Asked Questions on Brackets
What do brackets mean in math?
Brackets in math are used to group expressions together. They are the first order of operation, therefore, the numbers in the bracket must be solved before we proceed with other parts of the equation.
What is the difference between parentheses, curly brackets, and square brackets?
Parentheses () are the most common types of brackets. The curly brackets {} are used to group sets of numbers and the square brackets can be used to group different sub-equations or to encapsulate a large equation.
What is the order of operations for brackets?
For the bracket types, we solve the parentheses first, then the curly brackets, and lastly, the square brackets.
[{()}].
Brackets in math: worksheets
Understand brackets now? Well, you can learn even more about them with Brighterly’s free worksheets:







