Circle Theorems: Definition, Formulas, and Examples
reviewed by Jo-ann Caballes
Updated on October 21, 2024
Welcome to Brighterly, where we make complex math concepts simple!
Today, we’ll be delving into the world of geometry and shapes and looking at circle theorems.
There are 8 different circle theorems geometry that we’ll explore today.
Here, we’ll go through all circle theorems and how you can use them to work out different types of angles in a circle. We’ll also share examples, plus practice questions and fun worksheets.
Consider this your cheat sheet circle theorems!
Circle theorems in geometry: definition
The definition of circle theorems geometry are theories that explain different angle properties within a circle. The circular angle definition is an angle created within a circle by a chord, tangent or radius, and circle theorems allow us to understand how they work and calculate missing angles – even without a protractor!
8 circle theorems
There are 8 main geometry circle theorems that we’ll cover today. Each of the circle theorem rules are different:
- Angle at the center theorem
- Angles in the same segment theorem
- Cyclic quadrilateral theorem
- Angle in a semicircle theorem
- Tangent-radius theorem
- Chord of a circle theorem
- Alternate segment theorem
- Angles inside the circle theorem
Circle theorem #1: Angle at the center theorem
The angle at the center circle theorem states that the angle at the center of a circle is twice the angle at the circumference.
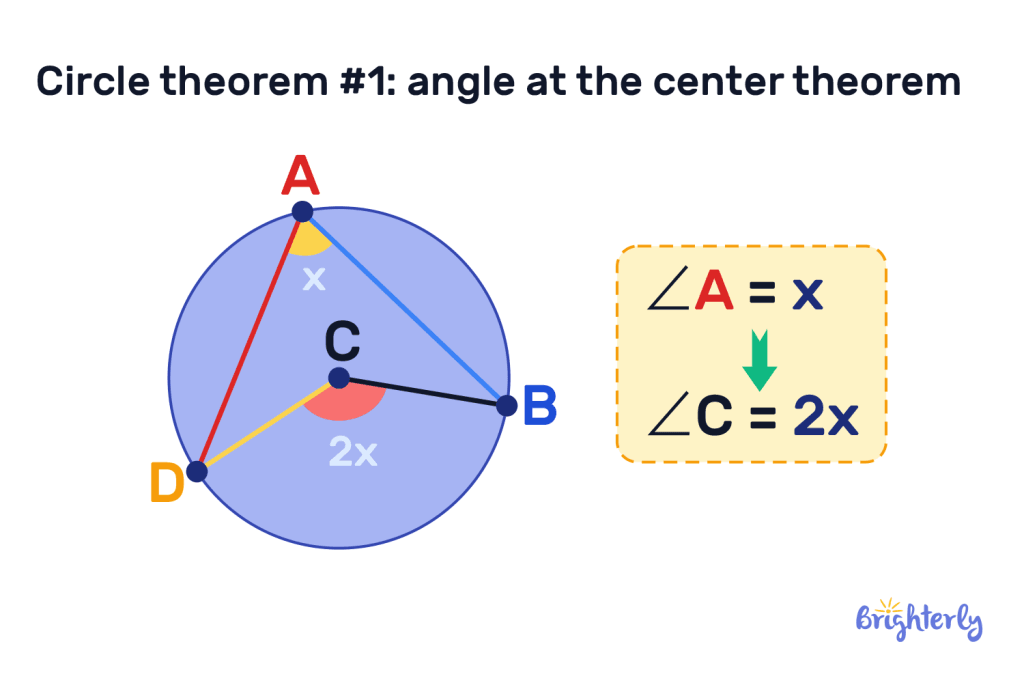
If we use the angle above, points B and D are both connected to A and C, creating two angles. The angle of BCD is exactly twice the size of the angle ABD, so we can see that the theorem is proved here.
For this theorem to work, there must always be at least 1 chord line that reaches from one part of the circumference to another part.
Circle theorem #2: Angles in the same segment
The angles in the same segment theorem states that angles at the circumference of the circle that are subtended by the same arc in the same segment are equal to one another.
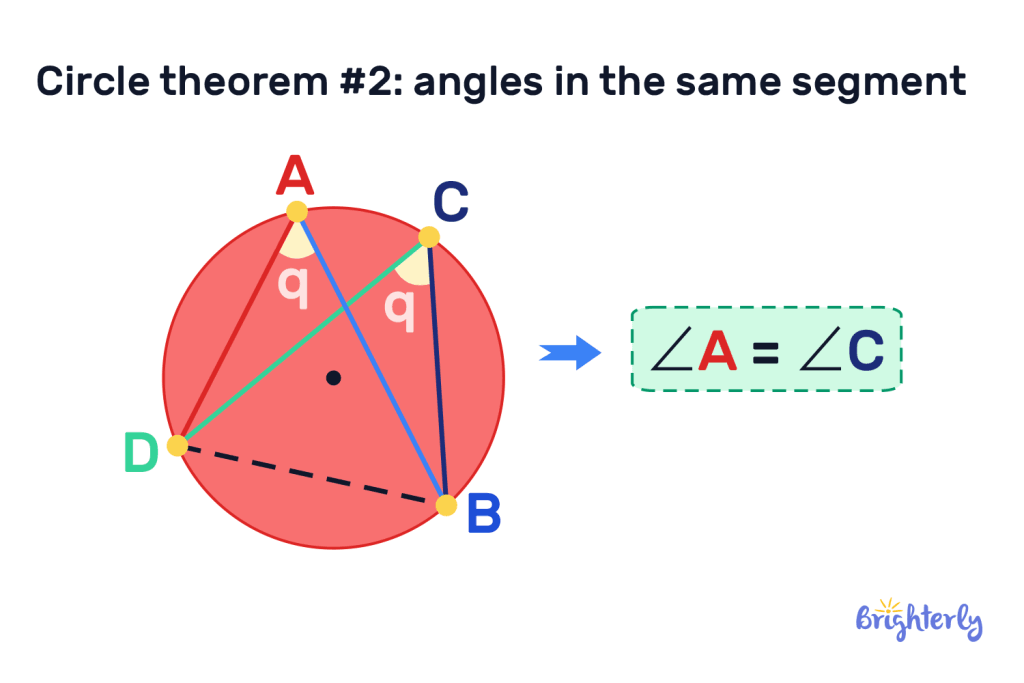
In the above example, we can see that a chord (DB) has been created to divide the circle into two segments: minor and major. A and C are then both connected to D and B by two more chords. You’ll see that both angles DAB and DCB are both equal. This would be true for any other angles created in this major section, proving the circle theorem that angles in the same segment are equal.
If one of our angles were in the minor segment, it would be different to angles in the major segment. However, if we had multiple angles in the minor segment, they would be the same as one another.
Circle theorem #3: Cyclic quadrilateral
The cyclic quadrilateral describes a quadrilateral (a four-sided closed shape) that can be inscribed inside the boundaries of a circle. In these cyclic quadrilaterals, the opposite angles will always add up to 180°.
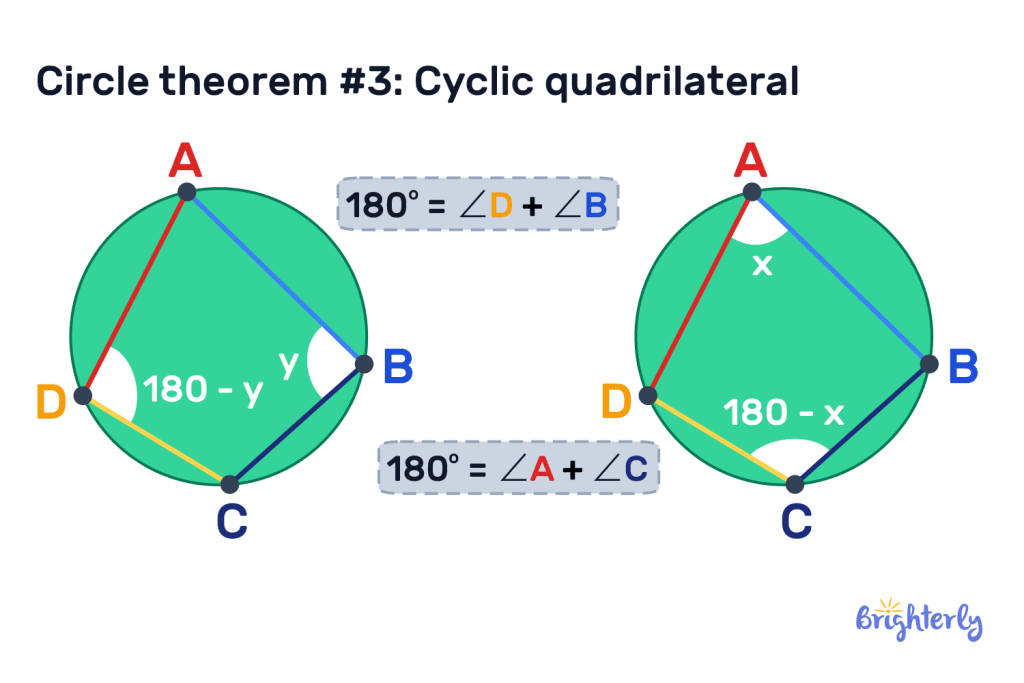
You’ll see from this circle theorem example above that both opposite sets of angles combine to make up 180°. This means, like all quadrilaterals, all cyclic quadrilateral internal angles will add up to 360°.
Circle theorem #4: Angle in a semicircle
The angles in a semicircle theorem states that angles created within the boundaries of a semicircle are 90°.
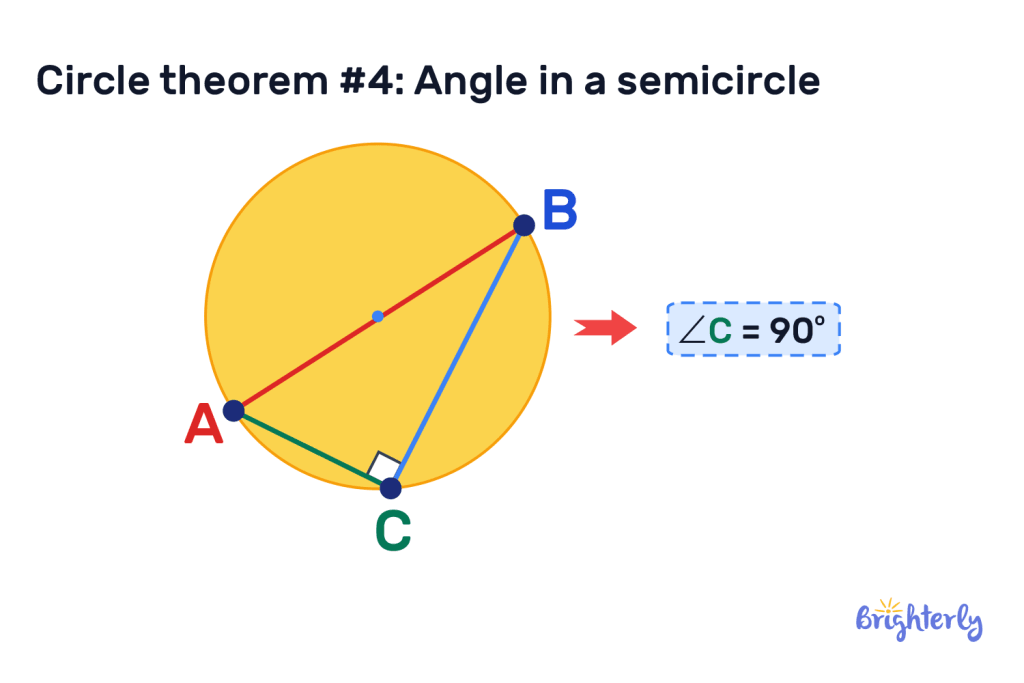
To show this circle theorem, a chord must be drawn through the center of a circle to divide it into two. Then, you place a point on the circumference within your semicircle and draw two more chords to connect to it. The angle created by these additional chords will always be 90°, no matter where in the semicircle you draw it.
Circle theorem #5: Tangent-radius
The tangent-radius theorem covers multiple key angles in a circle rules.
The first is that the angle between the radius and a tangent will always be 90°. To see this in action, draw a straight line from the center of your circle to only one point on the circumference – in contrast to a chord, this line will only go through half of your circle. Next, draw a tangent outside your circle that will also meet that same point on the semicircle. The angle created by these two lines will always be 90°.
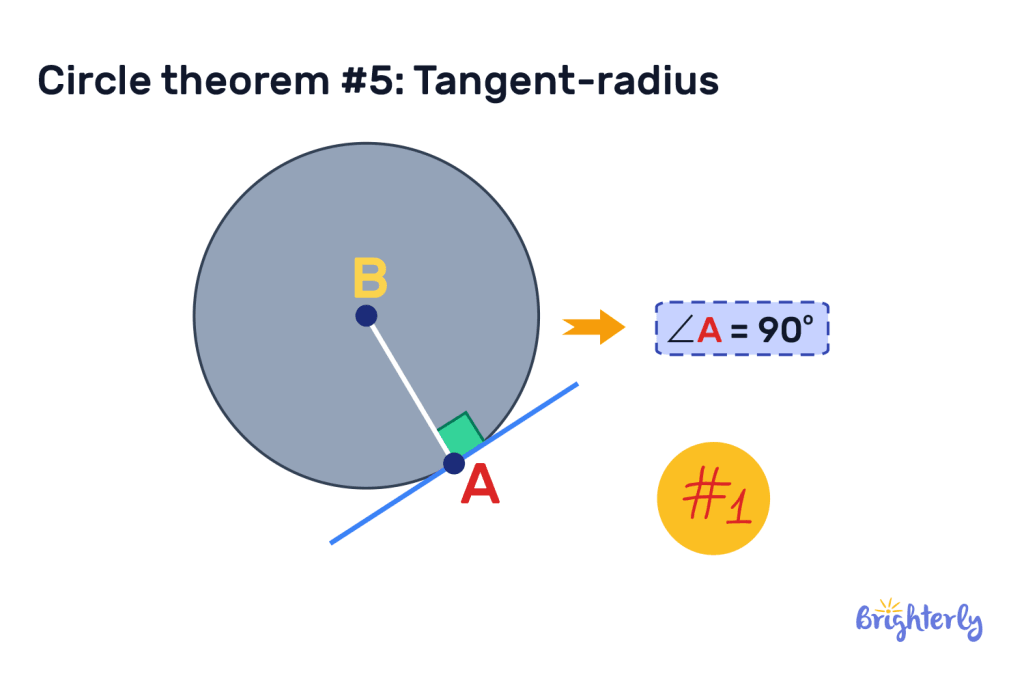
The second part of this circle theorem is that tangents that meet at the same point will always be equal in length. If you identify two points on the circumference of your circle and join them together with a line segment, the lines will both be the same length.
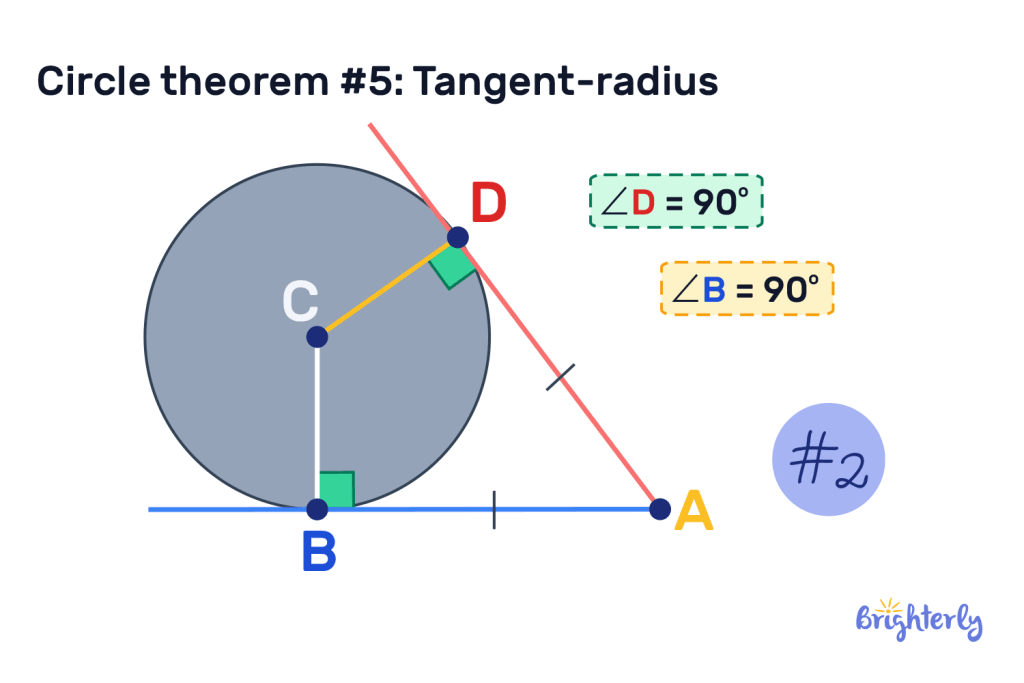
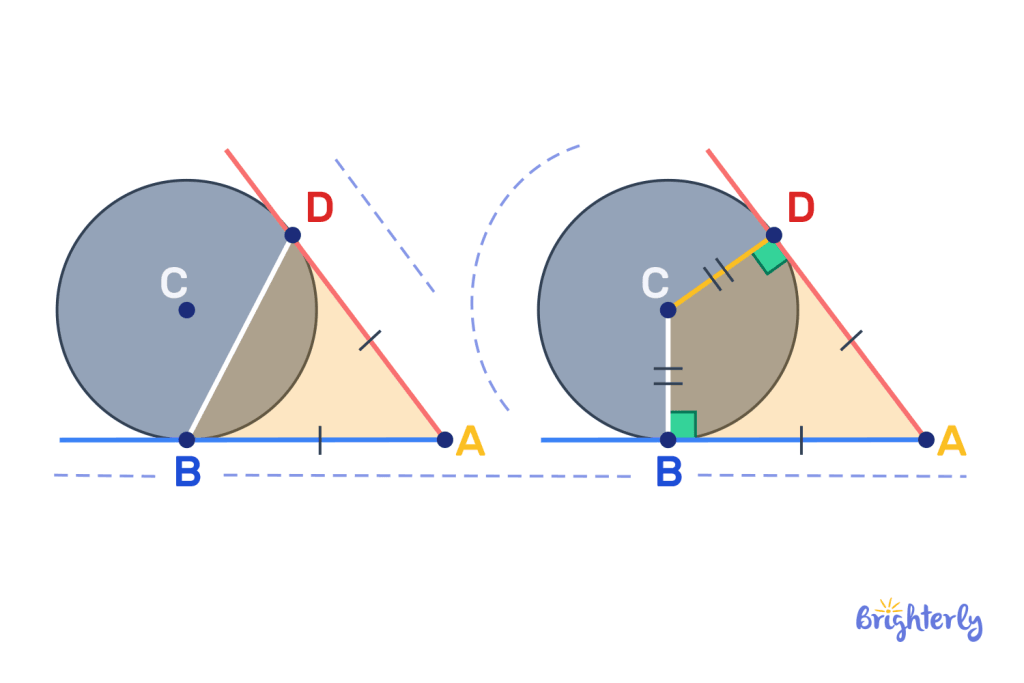
Additionally, using these two tangents, we can create two different shapes with different angles in a circle rules. If we connect both points on the circumference via a chord, we will always create an isosceles triangle. If we create two radius lines that connect our points to the center, we will always create a kite.
Circle theorem #6: Chord of a circle theorem
The chord of a circle theorem dictates how chords and radius lines interact with one another when they intersect. This theorem states that when a radius bisects a chord in a circle, it will always create right angles.
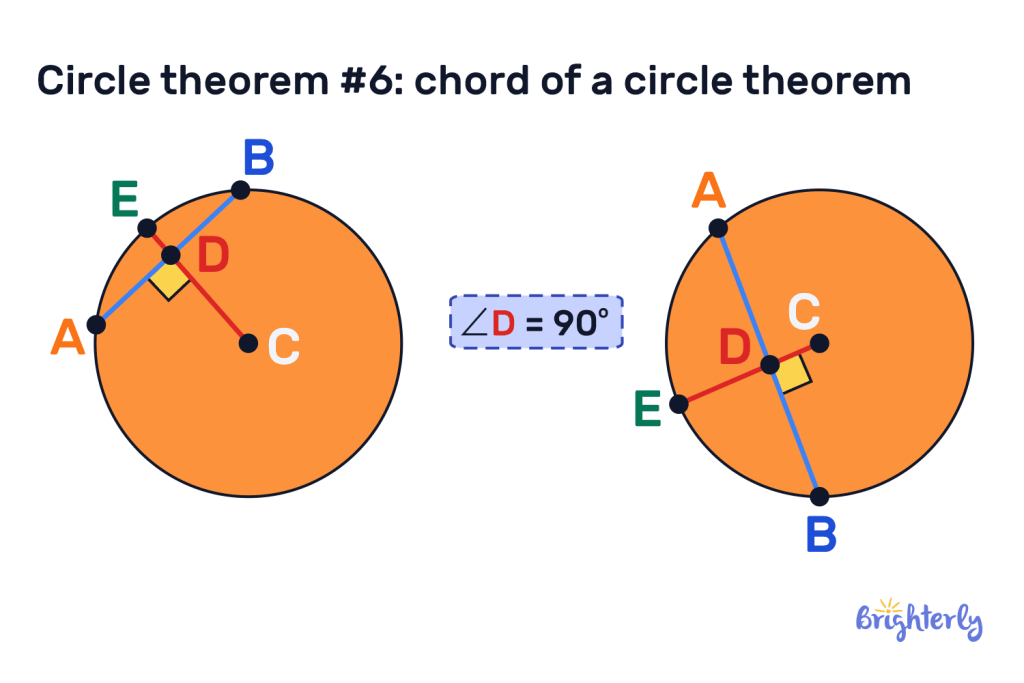
This theorem will always be true, no matter where in the circle your intersecting chord and radius are placed, as we can see from the examples above.
Circle theorem #7: Alternate segment
This circle theorem refers to how tangents and chords interact with one another and the angles they create when intersecting. It states that the angle between a chord and a segment will be equal to the angle created in the alternate segment.
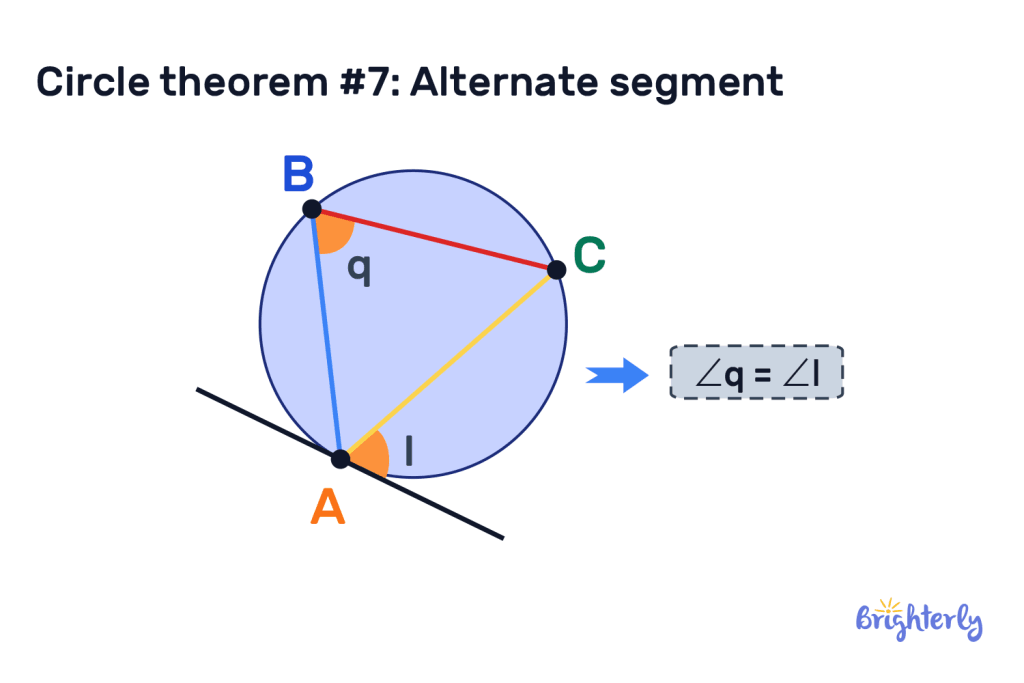
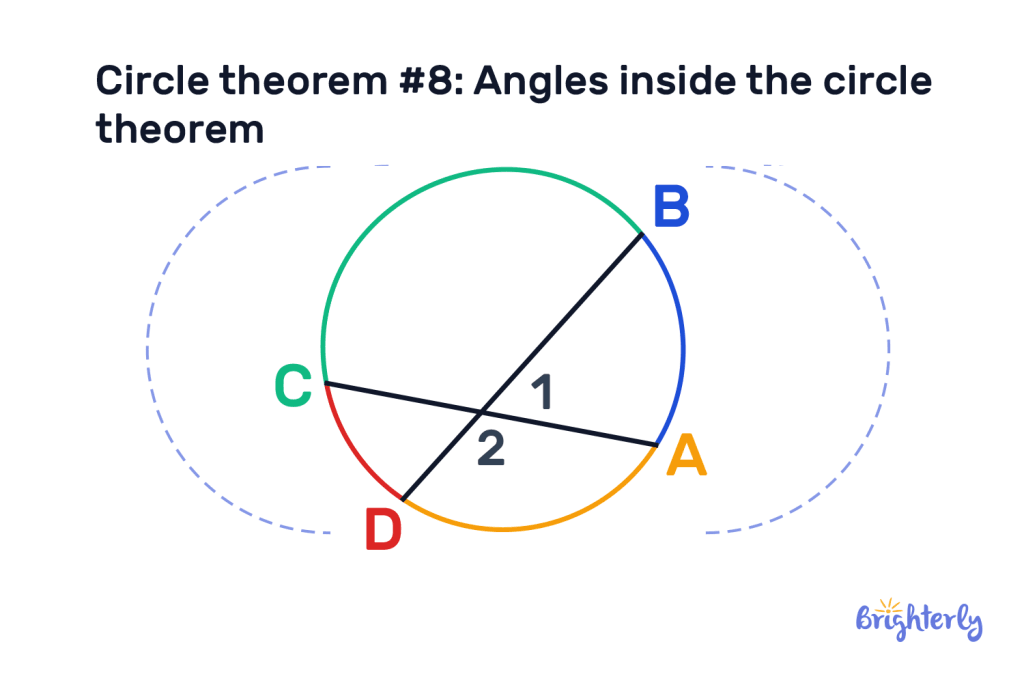
Circle theorem #8: Angles inside the circle theorem
The angles inside the circle theorem is straightforward and states that the size of angles created by two chords intersecting within a circle are half the size of the arcs intercepted by the angles and their vertical angles.
Circle theorems formulas
There are a range of formulas that can support circle theorems, including standard circle formulas and angles in circles formulas.
Circle formulas
To work with circle theorems geometry, it’s helpful to know the key circle formulas:
- Circumference of a circle: 2 × π × radius
- Length of an arc: (central angle made by the arc ÷ 360°) × 2 × π × radius
- Area of a circle: π × R²
- Area of a sector: (Central angle made by the arc/360°) × π × R²
Central angle of a circle formula
To calculate the angle between two radius lines in a circle, you’ll use the central angle of a circle formula.
These angles in circles formulas can be expressed as:
Central angle, θ = (Arc length × 360º) ÷ (2πradius) degrees
or
Central angle, θ = Arc length/radius
Angle in a semicircle formula
You can use the following angles in circles formula to work out the angle in a semicircle:
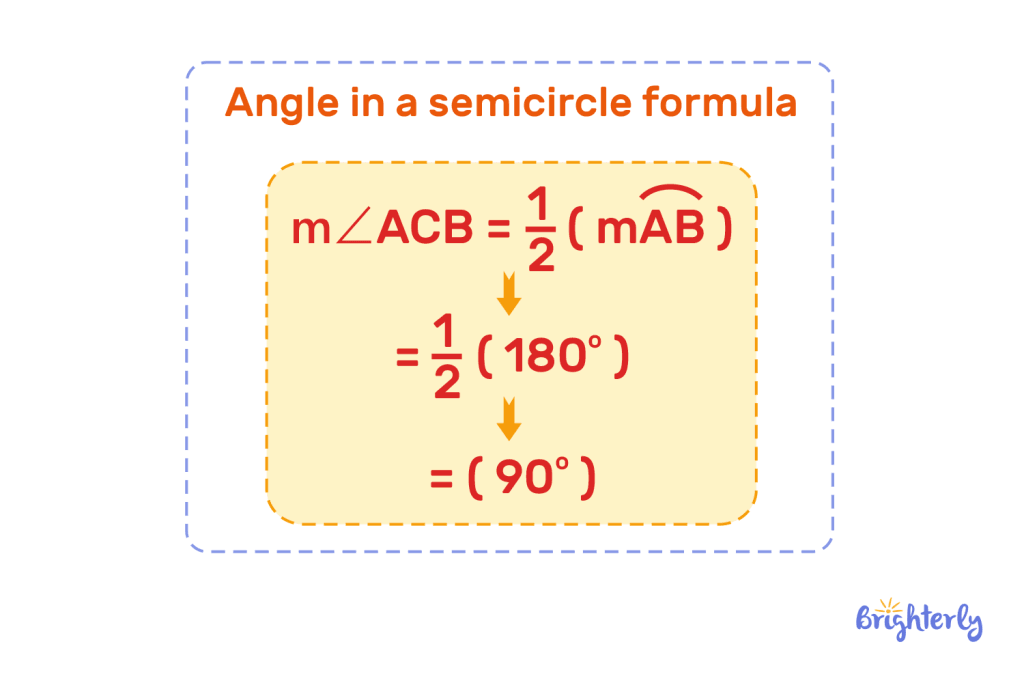
Angles in the same segment formula
Use this formula to work out angles in the same segment:
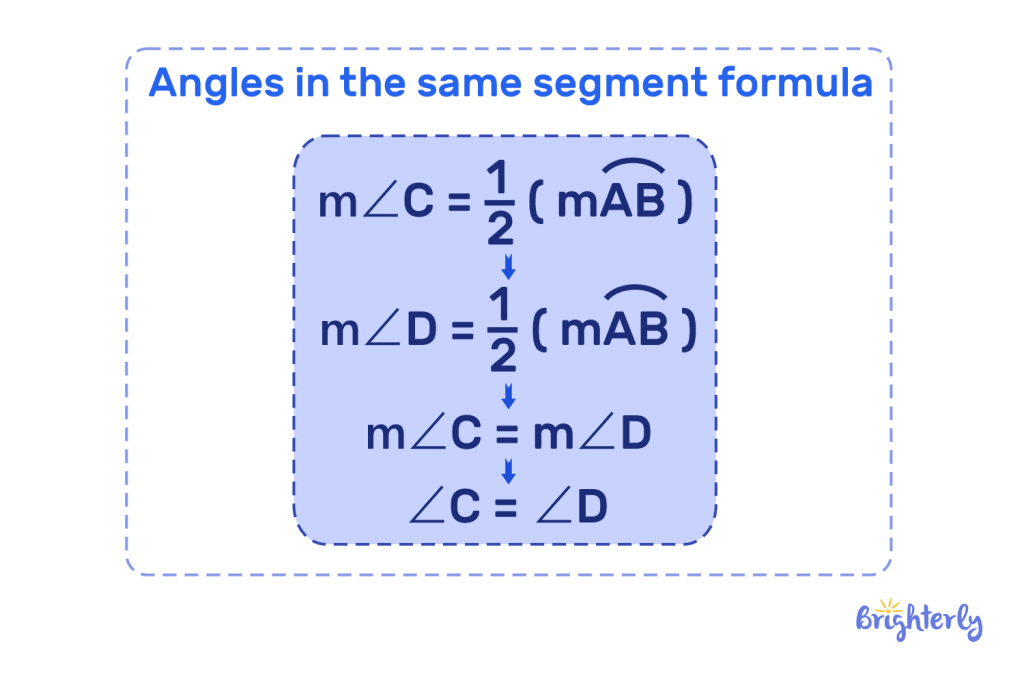
Cyclic quadrilateral formula
You can use the following formula to work out cyclic quadrilateral angles:
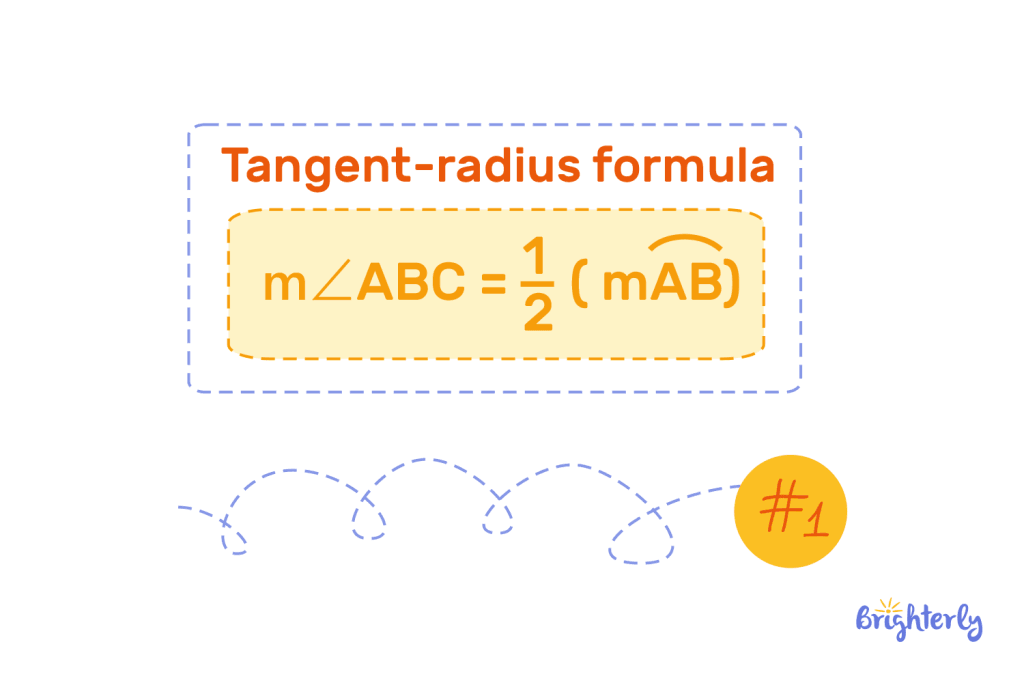
Tangent-radius formula
This angles in circles formula works with the tangent radius theorem to work out your angles within your circle:
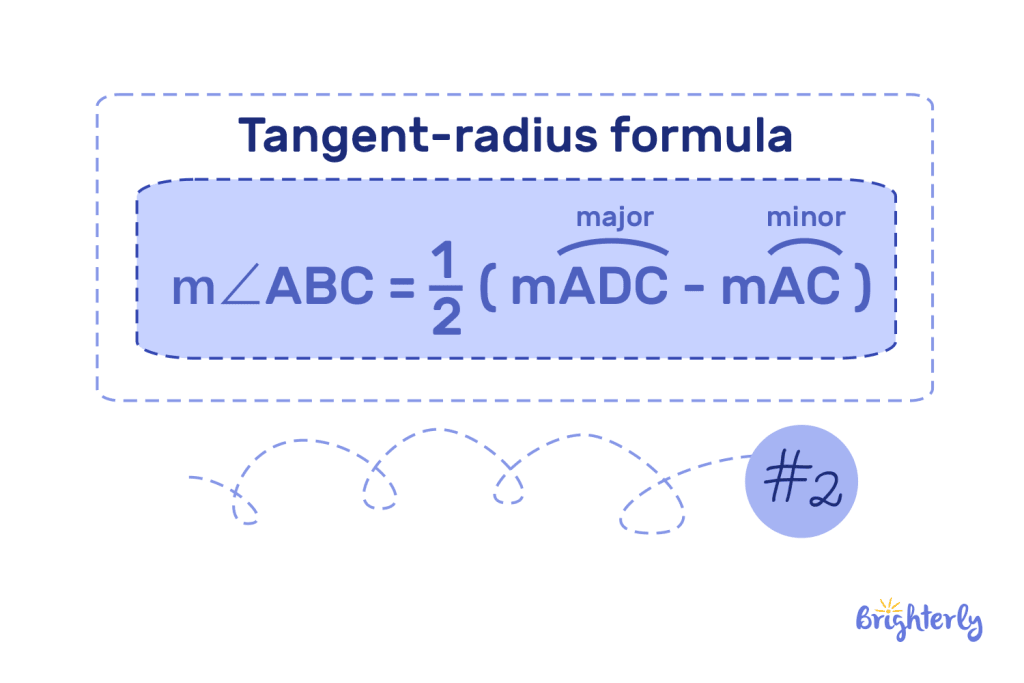
For angles outside of your circle, use this formula:
Solved math tasks: examples
Time to put your knowledge of geometry circle theorems to the test with our solved math tasks! Complete each task then review the answer to see if you’re correct.
Solved math task 1
Using the angle in a semicircle theorem, work out the angle of a:
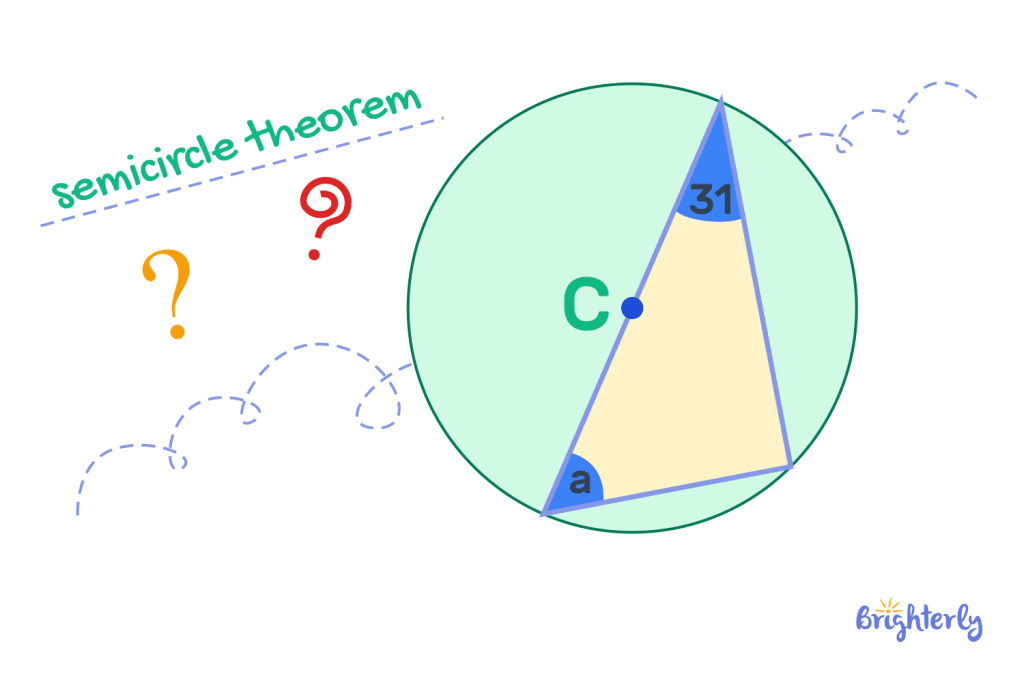
Answer:
| 59°. |
We know from the circle theorem that the remaining angle is 90°, so to work out this angle, we remove the two known angles from 180°.
180° – 90° – 31° = 59°
Solved math task 2
Using the angle at the center theory, work out angle e:
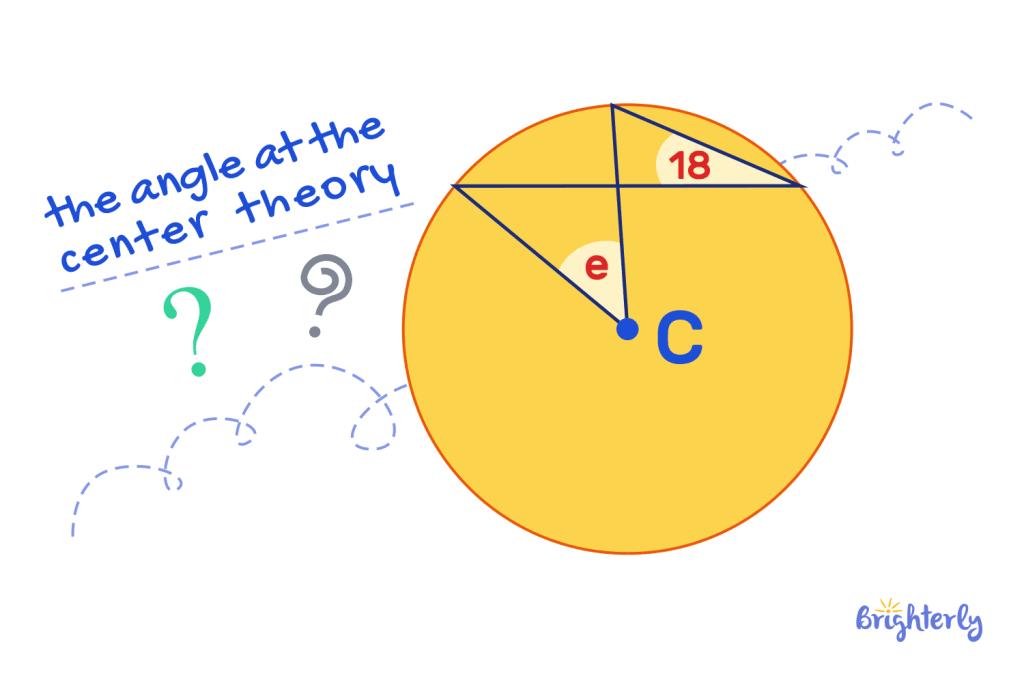
Answer:
| 36° |
We know from the circle theorem that the angle at the center is twice the angle of the circumference, so we double the known angle.
18° x 2 = 36°
Circle theorems: practice math problems
Circle theorems: worksheets
Want to become a master at circle theorems? Check out our cool math worksheets to become a geometry whizz!
Math homework help for grade 1-8
Get the homework support your child needs!
Choose kid's grade
Math Program
Boost Your Child's Math Abilities! Ideal for 1st-8th Graders, Perfectly Synced with School Curriculum!
