• Math tutors
• /
• Knowledge Base
• /
• Cone – Definition With Examples

Cone – Definition With Examples

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on November 12, 2024

Cones are one of many three-dimensional shapes. Here, we will discuss the definition of a cone, talk about the attributes of a cone, and treat the examples of cones, along with practice questions and relevant worksheets.

What Is a Cone?

A cone is a 3d shape with a circular base and a pointed tip which is called the vertex or apex. 

Cone definition

A cone in math is a three-dimensional solid shape with a circular base that leads to a pointed pinnacle known as the apex. 

The cone in geometry, like other three-dimensional shapes, has multiple areas — two areas to be exact. The two areas are the total surface area and the curved surface area.

The total surface area is the cumulative area of the base from its vertex to the circular base. The curved surface area, on the other hand, is the area of just the curved surfaces of the shape.

What are the attributes of a cone?

Now that we’ve defined a cone, the easiest way to identify the shape is by its curved surface, circular base, and pointed tip. However, the cone has some other cone attributes that make it unique. Here are some of them: 

• The cone has 1 edge which is the meeting point of the circular base and the curved surface.
• It has two faces: the flat circular surface at the bottom and the curved surface at the side that leads up to the tip.
• There are three parts of a cone — radius, height, and slant height. 

The radius is from the center of the base to any point in the circumference.

The height is the distance from the center of the base to the vertex of the cone.

The slant height is the length from the peak of the cone to the edge outside the base of the cone.

Cone examples

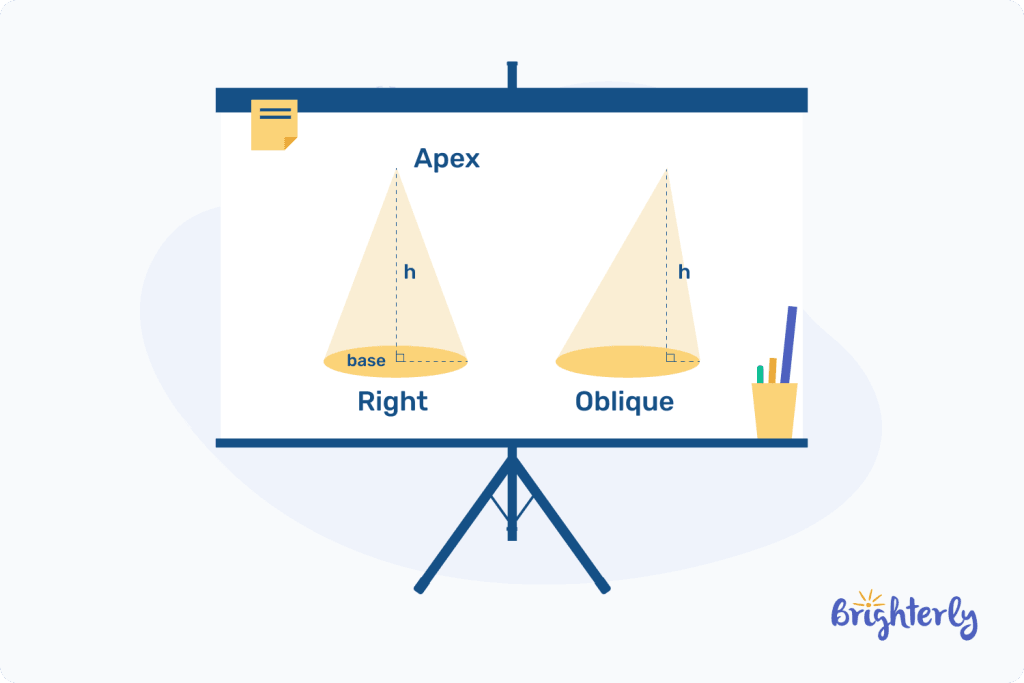
Cone shape examples can appear in two forms: A right circular cone and an oblique cone. The difference between these two is the location of the apex to the base:

Right circular cone:

Here, the distance from the apex of the cone to the center of the base (the axis) is perpendicular which forms a right angle if you draw a line to trace the apex to the center of the base. The vertex is directly above the middle of the base, meaning this is the most common example of a cone as we see in daily life such as the traffic cone.

Oblique cone:

The oblique cone is like the right circular cone except that the apex is not directly above the center of the circular base. This cone has a skewed appearance.

Cone formulas

There are formulas for determining the total surface area of a cone, its curved surface area, volume, and slant height. Here are the formulas for cone:

Slant Height of a cone

The formula for the slant height of a cone is the square root of the square of the radius plus the square of the height. It is derived from the Pythagoras theorem. 

It is expressed as: 

Curved surface area 

Remember that a cone has two surface areas: the flat and curved surface area. The curved surface area is the part that wraps around the upper part of the cone and leads to the vertex. 

To find the curved surface area, we multiply the radius by the slant height of the cone and pi (π). 

Therefore, the formula is expressed as;

CSA =  π ✕ r ✕ l 

Don’t forget that π = 3.14

Total surface area

As we mentioned earlier, the total surface area is the cumulative area of the cone. Its formula is the summation of the curved surface area and the circular base area.

Note that the circular base area is π ✕ r²

Therefore, total surface area = circular surface area + circular base area

OR

TSA = π ✕ r ✕ l + π ✕ r² square units 

Volume of a cone

Volume is the quantity of space occupied by an object. The volume of a cone is the space the shape occupies or how much capacity it can contain.

We find the volume of the cone by multiplying ⅓ by π, the square of the radius, and the height of the cone.

Thus, V = ⅓ ✕ (π ✕ r² ✕ h) cubic units.

Cone real-life examples

A cone looks like a circle and a triangle put together to form another shape, and we see it literally everywhere. Here are some cone shape examples in real life: 

• A traffic cone — it’s in the name!
• An ice cream cone
• A camping tent 
• Party hats
• Megaphone
• Funnel

Solved Math Tasks: Examples

Solved math problem 1

When the radius of the base of a cone is 5 cm and the slant height is 25 cm, what is the curved surface area?

Answer

Remember that CSA = π ✕ r ✕ l which means:

CSA = 3.14 ✕ 5 ✕ 25

= 392.5 cm²

Solved math problem 2

What is the total surface area of a cone when it has a slant height of 38 cm and a radius of 6 cm?

Answer

TSA = π ✕ r ✕ l + π ✕ r²  and when converted, it becomes:

Solved math problem 3

How much can a cone have as its volume when the radius is 7 cm and the height is 30 cm?

Answer 

V = ⅓ ✕ (π ✕ r² ✕ h) 

V = ⅓ ✕ (3.14 ✕ 7 ✕ 7 ✕ 30)

V = ⅓ ✕ (4615.8)

Cone: Practice Math Problems

Cone: worksheets

Ice cream cones, party hats, traffic cones, and more, are some of the real-life cone examples we see every day. To better understand this shape, we explain the cone as a 3d shape,  formula for cone, and give examples, too.

Children can understand cones and the structural world of geometry better through our free worksheets:

• Surface area and volume worksheets
• 2d and 3d shapes worksheets 
• 3d shapes worksheets

Jessica Kaminski

72 articles

Jessica is a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.