Cos2x – Formula, Identity, and Solved Math Tasks
reviewed by Jo-ann Caballes
Updated on March 10, 2026
Cos2x is a trigonometric function that gives the value of cosine when the angle is 2x.
In this article, we’ll cover the definition of cos2x and its formulas, derivations, properties, cos 2x identity, and relation to other trigonometric functions. We’ll also share cool math worksheets and practice test questions for you to cement your learning!
What is cos2x?
Cos2x is the cosine of double the angle. ‘Cos’ stands for cosine, which is a key function in trigonometry. The 2x refers to the angle being doubled.
Definition of cos2x
The definition of cos2x in trigonometry is a function that represents the cosine of twice any given angle (x). The cos2x identity is also called the double-angle identity of the cosine function.
As an example, let’s say we want to find the cos2x trig identity of an angle that is 30°. Double that is 60°, so the cosine of that would be its cos2x value.
The cos 2x formula
There are 2 main types of formulas that determine what does cos2x equal. Here they are:
Formula in terms of cos(x)
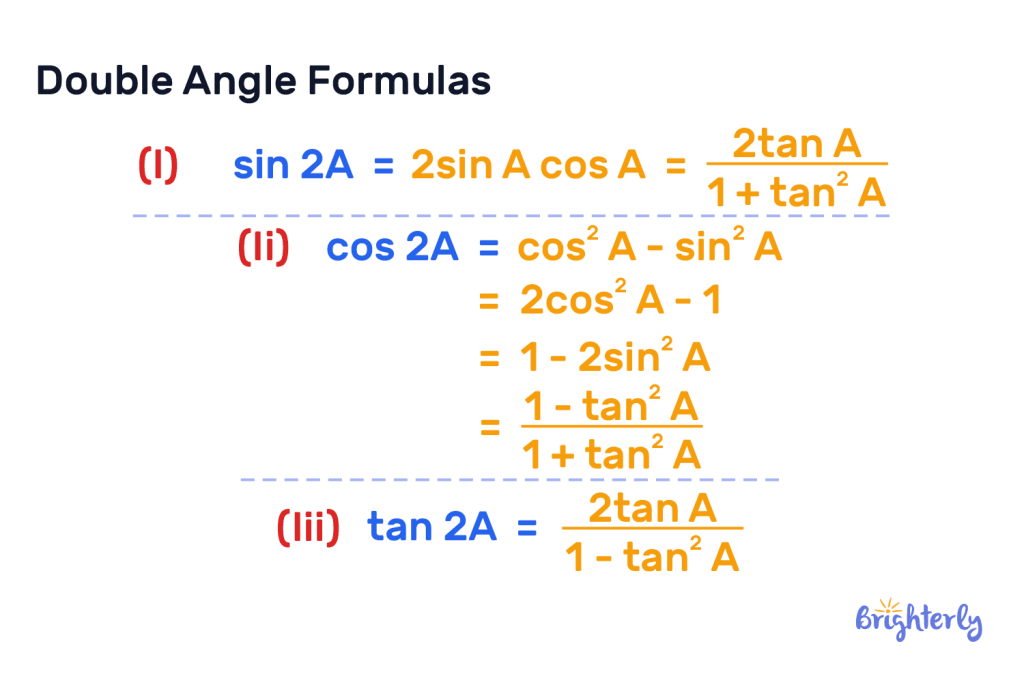
The formula of cos2x in terms of cos(x) is cos(2x) = 2cos²x – 1. We use this formula when we don’t know the value of sin(x).
Formula in terms of sin(x)
The formula of cos2x in terms of sin(x) is cos(2x) = 1 – 2sin²x. As you may have guessed, we use this value when we don’t know the value of cos(x).
Derivation of cos2x formula
Cos2x derivative means showing how the formula is obtained from basic trigonometric identities. There are two ways you can do this:
Derivation using the cosine rule
The derivation using the cosine rule takes us back to the concept of the unit circle and the basic definition of cosine. We derive the formula of cos2x by applying the cosine rule to an appropriate triangle, furthering our understanding of how this function behaves.
Derivation using double-angle identity
We can also apply derivation using double angle identity by using a little more algebraic manipulation. This has the same result and again aids in our understanding of cos2x’s properties and behavior. It also relates to the cosine-squared identity.
Cos2x in relation to other trigonometric functions
Cos(2x) function is not an isolated one. Cos 2x trig identity is closely connected to other trigonometric identities. Using the Pythagorean identity sin²x + cos²x = 1, we can rewrite it in different forms:
- cos(2x) = cos²x − sin²x
- cos(2x) = 2cos²x − 1
- cos(2x) = 1 − 2sin²x
It is also related to tangent through the following cos(2x) identity:
cos(2x) = (1 − tan²x) / (1 + tan²x)
This connects it indirectly to secant since 1 + tan²x = sec²x.
Through these relationships, we can also use cos2x to rewrite expressions and solve trigonometric equations.
Cos2x and sin2x
In relation to sin2x, the cos(2x) identity can be seen in the equation cos²x+sin²x = 1. This equation represents the Pythagorean trigonometric identity. When we subtract cos2x from either side in this formula, it becomes sin2x + cos2x -cos2x = 1 – cos2x, which can be simplified as sin(2x) = 2sinx cosx.
Cos2x and tan2x
We can use cos2x in terms of tan x. In fact, even without knowing the exact values of cos(x) or sin(x), we’re able to identify cos2x. We do this by amending the cos2x formula with tan2x.
Cos2x and sec2x
The reciprocal of sec(x) is cos(x), meaning that these two trigonometric functions are also related, and we can easily solve any equations involving both functions.
What does cos^2x equal?
The expression cos²x means (cosx)2, or cosine multiplied by itself. While it may look simple, we can rewrite cos²x in several useful ways using trigonometric identities.
From the Pythagorean identity sin²x + cos²x = 1, we can express it as:
cos²x = 1 − sin²x.
We can also use the double-angle one from cos2x identities to also write:
cos²x = (1 + cos(2x)) / 2.
These equivalent forms can come especially handy when you are solving trigonometric equations, simplifying expressions, or working with integrals. Knowing how to rewrite cos²x will let you move between different trig functions more easily and make many problems much simpler to handle.
Trig identity of cos2x
Basic identity
The cos2x basic identity can be defined by its formula in trigonometry: cos(2x) = cos²x – sin²x. This formula is a foundational part of trigonometric equations.
Double-angle identity
The cosine function can also be known as the double-angle identity. We can describe the cosine of a double angle in terms of the cosine and sine functions in trigonometry. It is also related to the cos-squared identity.
The double-angle identity of cos 2x is an expansion of its basic identity. It provides us with three equivalent forms, aka what is cos^2x equal to: cos(2x) = cos²x – sin²x = 2cos²x – 1 = 1 – 2sin²x. We can see the versatility of cos2x through these cos 2x identities, which allow us to express it in terms of a single trigonometric function, either cosine or sine. This also relates to the cos-squared identity.
Multiple-angle identity
We can generalize the multiple-angle identity from the double-angle identity. For example, the double-angle formula cos(2x) = 2cos²x − 1 shows how we can rewrite the cosine of a larger angle in terms of cos x.
We can also expand this idea further to expressions like cos(3x), cos(4x), and beyond, which lets us express trigonometric functions of multiple angles using powers of sine or cosine.
Properties of cos2x
The properties of cos2x help us to identify and understand it. It has properties in two key areas:
Properties of cos2x in trigonometric functions
When it comes to trigonometric functions, cos2x has the ability to show the recurrence of cosine. This recurrence means it repeats its values every 360 degrees or 2π radians. It also shows the fact that the cosine function is even – i.e., cos(2x) = cos(-2x), meaning it can make calculations simpler.
Properties of cos2x in even and odd functions
Because cosine is even, this means cos2x is even too. In other words, it doesn’t change if we use x or -x. When working with negative angles, calculations become much easier thanks to cos2x.
Writing equations using cos2x
There is some information you need to know when it comes to writing both simple and complex equations using cos2x. We cover this below.
Simple equations involving cos2x
Simple equations involving cos2x are fairly straightforward to write and work with. If we use the example of cos(2x) = 0, we’ll show you how. To solve, simply find the value of 2x, then half it (aka divide by 2) to solve for x.
Complex equations involving cos2x
Complex equations involving cos2x require an understanding of concepts like trigonometric identities. Once you understand these concepts, you can easily solve more complex cos2x equations. Let’s use the example of the equation 2cos²x – 1 = sin(x). Knowing the double angle identity, we can substitute cos(2x) in for 2cos²x – 1, simplifying our equation and making it easier to solve.
Practice problems on cos2x
Simple practice problems
Simple practice problem 1
Find the value of cos2x when x = 30 degrees.
Solution:
Because cos2x means finding the cosine of double the angle, we know that 2x = 60 degrees.
Next, we know that cos(60 degrees) = ½, thanks to the standard values of trigonometric functions.
| So, to solve, cos(2*30 degrees) = cos(60 degrees) = 1/2. |
Simple practice problem 2
Evaluate cos2x when x = 45 degrees.
Solution:
Doubling the angle gives us 2x = 90 degrees. Now, cos(90 degrees) = 0.
| So, cos(2*45 degrees) = cos(90 degrees) = 0. |
Complex practice problems
Complex practice problems 1
Solve the equation cos(2x) = cos(x) for x in the interval [0, 2π).
Solution:
This equation is true when 2x = x + 2nπ or 2x = -x + 2nπ, where n is an integer.
The first equation simplifies to x = 2nπ. In the interval [0, 2π), this gives us the solutions x = 0 and x = 2π.
The second equation simplifies to 3x = 2nπ, which gives x = 2nπ/3. In the interval [0, 2π), this gives us the solutions x = 0, x = 2π/3, and x = 4π/3.
| So the solutions to the equation cos(2x) = cos(x) in the interval [0, 2π) are x = 0, x = 2π/3, x = 4π/3, and x = 2π. |
Complex practice problems 2
Solve for x in the equation 2cos²x – 1 = sin(2x) in the interval [0, 2π).
Solution:
This equation can be rewritten using the double angle identities as cos(2x) = sin(2x). This equation is true when 2x = π/4 + nπ. Simplifying, we get x = π/8 + nπ/2.
| The solutions to this equation in the interval [0, 2π) are x = π/8, x = 5π/8, x = 9π/8, and x = 13π/8. |
Cos2x: Practice Math Problems
Cos2x: worksheets
Now that you’ve learnt about cos²(x) identity, formulas, and more, it’s time to build on that knowledge. We have many free math worksheets for you to explore, which cover important geometry and trig topics:
- Trigonometry worksheets
- Area and circumference of a circle worksheets
- Angles in a triangle worksheets
- Missing angles in a triangle worksheets
Make sure to download them and have a look!
Frequently asked questions on cos2x
What does cos2x represent?
Cos2x represents the cosine of the double of an angle. This means that cos2x is the cosine of the angle that is twice as large as any given angle, which we’ll call x.
What is the formula for cos2x?
There isn’t just one formula for cos2x. In fact, there are three formulas, all derived from the basic and double identities of cosine. The formulas are:
- cos(2x) = cos²x – sin²x
- cos(2x) = 1 – 2 sin²(x)
- cos(2x) = 2 cos²(x) – 1
How is cos2x used in real-world applications?
Cos2x has many applications in the real world. It is used in fields like computer science, engineering, and physics, and can be used to solve problems involving periodic motion, signal processing, wave function analysis, and even in the computation of certain types of integrals in calculus.
How can I solve equations involving cos2x?
You can solve equations involving cos2x in different ways, but you’ll need to understand algebraic manipulation and trigonometric identities. Depending on your equation, you may use Pythagorean identities (i.e., sin²x + cos²x = 1), the properties of even and odd functions, or double-angle identities to solve equations involving cos2x.
Is cos2x an even or odd function?
Cos2x is an even function. This means it has the property that cos(2x) = cos(-2x) for all x. This property is a result of the fact that the cosine function is even.
Is cos2x the same as cosx2?
No, they are different. Cos(2x) means the cosine of double the angle x, so the angle is multiplied by 2 before taking the cosine. In contrast, cos(x²) means the cosine of x squared. Here, you first square x, then take the cosine of that result.
Math & reading from 1st to 9th grade
Looking for homework support for your child?
Choose kid's grade
Math & Reading for Grades 1–9
Build real confidence for your child with a Brighterly math or reading tutor.
