CPCTC: Definition, Postulates, Theorem, Proof, Examples
reviewed by Jo-ann Caballes
Updated on November 15, 2024
Welcome to Brighterly, where learning mathematics is an exciting adventure!
Today, we’re going to delve into geometry and explore the concept of CPCTC!
In this article, we’ll explore the CPCTC meaning and what it stands for. We’ll also share practice test problems and math worksheets for you to test your knowledge!
What is CPCTC in geometry?
CPCTC in geometry is a theorem that relates to congruent triangles and their corresponding parts. CPCTC is an important element in geometry and our understanding of triangles.
So when do you use CPCTC? It can be used in many real-world scenarios including engineering, architecture and even art! Let’s see how we can define CPCTC below.
CPCTC: definition
The definition of CPCTC in geometry is a theorem that states the corresponding parts of two congruent triangles – i.e. the angles and sides that match – are also congruent. This is the CPCTC property. It’s a principle that’s widely used to solve problems and provide proofs in geometry.
This means if you have two triangles with equal lengths and angles (corresponding sides), they are congruent triangles.
What does CPCTC stand for?
CPCTC stands for ‘corresponding parts of congruent triangles are congruent’ – this phrase really does what it says on the tin!
CPCTC example
The best way to provide CPCTC examples is through a visual. In the CPCTC geometry examples below, you’ll see two congruent triangles. You’ll also see that their sides and angles are also congruent!
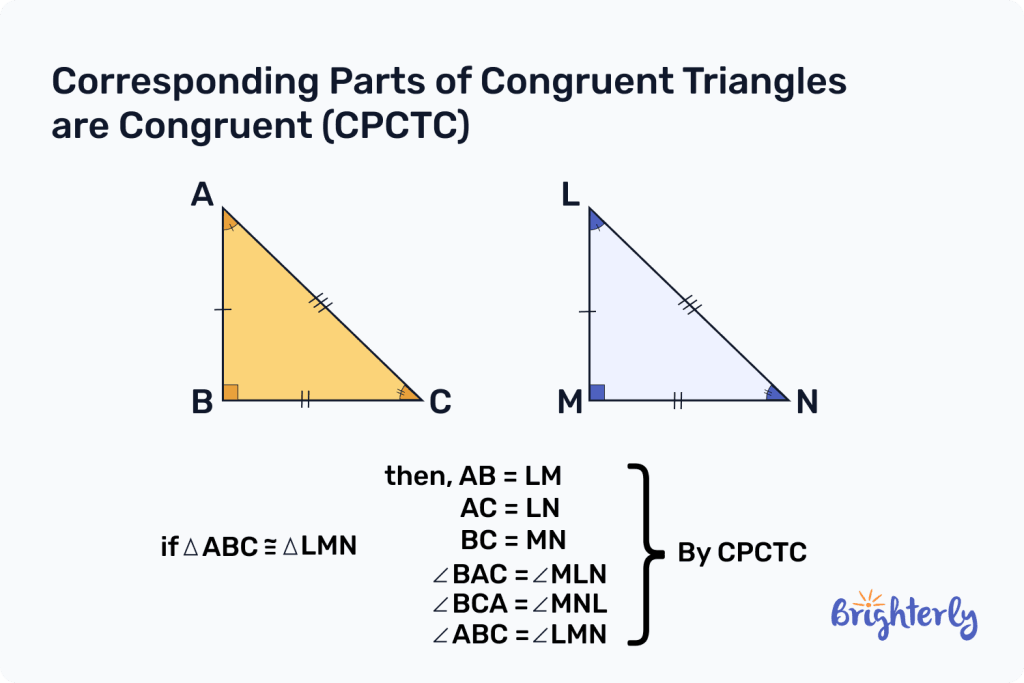
Congruent triangles
Congruent triangles in geometry are triangles that are identical to one another – meaning they have the same shape and size. If you placed one of the triangles on top of the other, they would match perfectly. To truly understand CPCTC in geometry, you need to be familiar with congruent triangles. Two triangles are congruent if they meet one of the following conditions (congruence rules):
- Side-Side-Side (SSS)
- Side-Angle-Side (SAS)
- Angle-Side-Angle (ASA)
- Angle-Angle-Side (AAS)
- Right angle-Hypotenuse-Side (RHS)
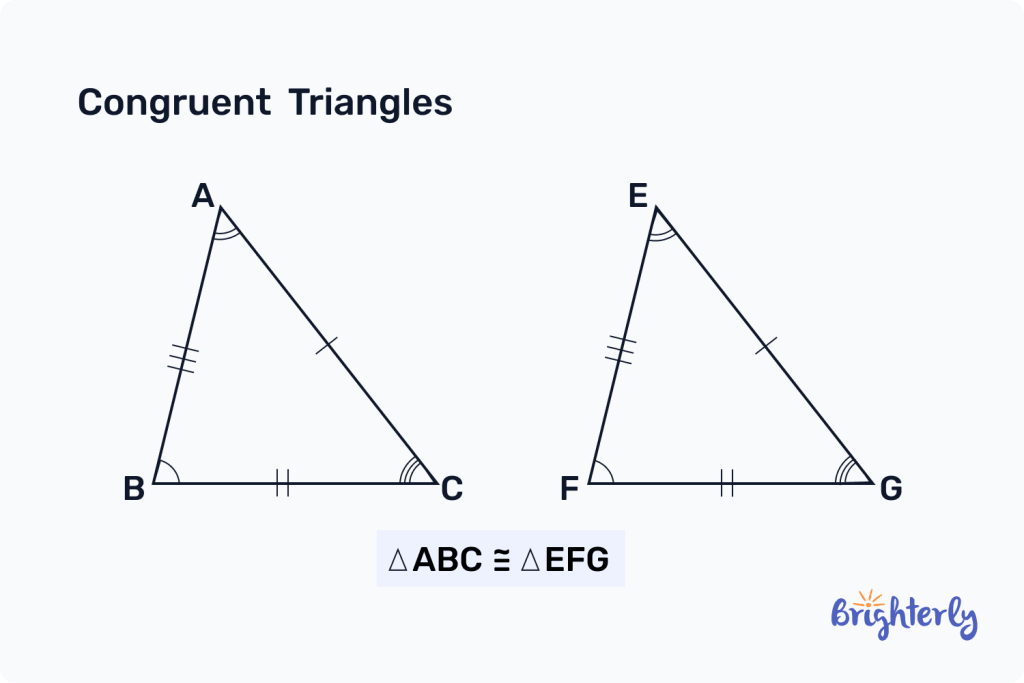
Corresponding parts
Corresponding parts are related specifically to congruent triangles. They refer to the sides and angles in triangles that are the same as one another. So your first angle in your first triangle is congruent to the first angle in your second triangle, the second to the second, and so on. The same applies to the sides of the triangles, making them equal in length.
CPCTC triangle congruence
CPCTC math is one method of proving that two triangles are congruent because if both the angles and the sides of two triangles are identical, then the triangle must be identical. By identifying if any of the congruence principles are true (SSS, SAS, ASA, AAS, RHS), we can prove their corresponding parts are congruent via CPCTC.
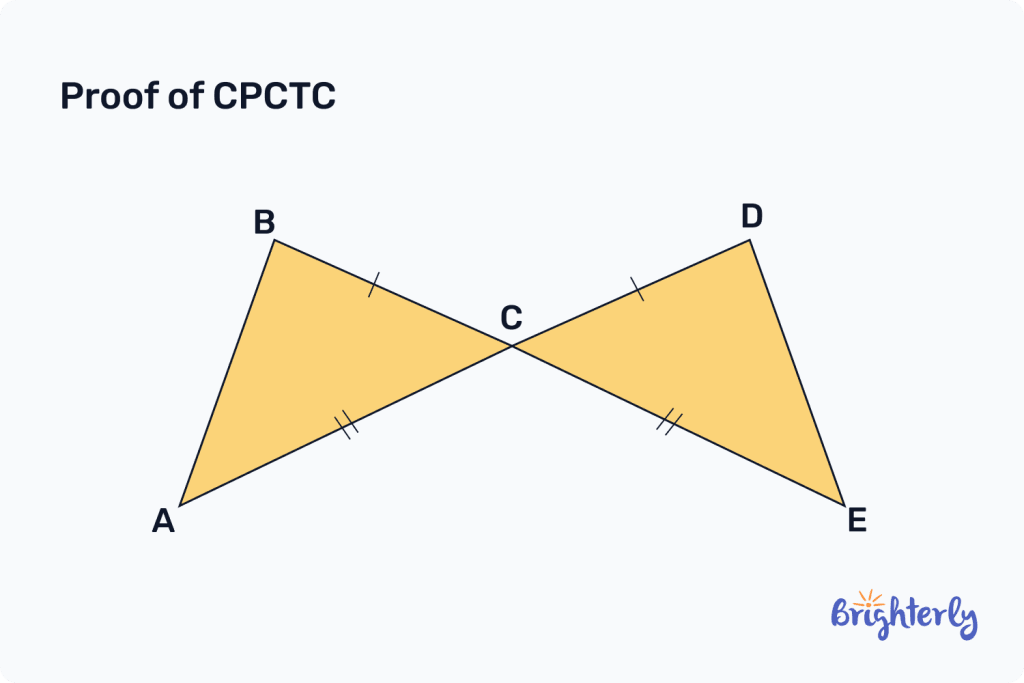
CPCTC proof
We can prove CPCTC in geometry through the theorems and postulates of geometry. Let’s dive into how exactly that works:
We have two triangles, Triangle ABC and Triangle DEF. We know they are congruent (using one of the congruence rules). By definition of congruence, the corresponding parts of these triangles are congruent. Therefore, we can say that ∠A ≅ ∠D, ∠B ≅ ∠E, ∠C ≅ ∠F, AB ≅ DE, BC ≅ EF, and AC ≅ DF.
Solved examples on CPCTC
Now you know all about CPCTC math, it’s time to test yourself! Answer our example questions and see if you get them right!
Solved math task 1
In two congruent triangles, ABC and DEF, ∠A = 40°, ∠B = 80°, and ∠C = 60°. Find the measures of ∠D, ∠E, and ∠F.
Answer:
∠D = ∠A = 40°, ∠E = ∠B = 80°, and ∠F = ∠C = 60°
Because the triangles are congruent, by CPCTC, the corresponding angles of the triangles will be congruent.
| Therefore, ∠D = ∠A = 40°, ∠E = ∠B = 80°, and ∠F = ∠C = 60°. |
Solved math task 2
In two congruent triangles, MNO and XYZ, M side length = 12 cm, N side length = 6 cm and O side length = 9 cm. Find the measures of the lengths X, Y and Z.
Answer:
X = 12 cm, Y = 6 cm and Z = 9 cm.
Because the triangles are congruent, by CPCTC, the corresponding lengths of the triangles will be congruent.
| Therefore, ∠D = ∠A = 40°, ∠E = ∠B = 80°, and ∠F = ∠C = 60°. |
Practice problems on CPCTC
CPCTC: worksheets
Ready to become even more of a whizz on CPCTC? Check out our cool math worksheets and practice your learning!
Frequently asked questions on CPCTC
What does CPCTC stand for?
CPCTC stands for ‘corresponding parts of congruent triangles are congruent‘. The full name accurately represents the CPCTC theorem that two triangles are congruent, and their corresponding parts (angles and sides) are congruent too.
What does CPCTC represent and when would you use it?
CPCTC represents ‘corresponding parts of congruent triangles are congruent’, and you would use it to prove that two congruent triangles have corresponding parts that are also congruent.
How is CPCTC used in geometry?
CPCTC helps us solve problems related to triangles in geometry. If we apply the theorem, we can make assertions about how equal corresponding parts in two triangles mean the two are congruent.
What are congruent triangles?
Congruent triangles are triangles that are identical – i.e. they have the same shape and size. If you placed one triangle over the other triangle, they would match perfectly.
How can I prove that two triangles are congruent?
You can prove two triangles are congruent through multiple methods, including Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), Angle-Angle-Side (AAS) and Right Angle-Hypotenuse-Side (RHS) congruence rules. By showing the corresponding parts meet one of these rules, you prove two triangles are congruent.
Why is CPCTC important in geometry?
CPCTC is important in geometry because it allows us to prove that triangles are congruent. It helps us understand the equality of corresponding parts, making it an important principle for proving theorems and solving geometric problems.
Can CPCTC be used in real-life applications?
Yes, CPCTC can be used in real-life situations. CPCTC can be used by engineers and architects to ensure the accuracy and consistency of corresponding elements in structures. By applying the principles of CPCTC, they can ensure that congruent components of a building or object fit together seamlessly.
How can I practice applying CPCTC?
You can practice applying CPCTC by using our worksheets, solved math problems and practice test problems, which provide real geometry tasks to practice on. You can then use hands-on activities like constructing real-life congruent triangles and analyzing their corresponding parts.
Problems with Geometry?
- Is your child finding it hard to master geometry concepts?
- An online tutor could be of assistance.
Choose kid's grade
Does your child need extra help with understanding geometry basics? Start studying with an online tutor.
