Denominator – Definition, Examples, Facts, FAQs
reviewed by Jo-ann Caballes
Updated on May 21, 2025
At Brighterly, we make mathematics simple, easy and fun for kids to learn.
As part of our series on fractions, we’re going to look at the denominator here.
In this article, we’ll cover the denominator definition and examples, answer questions and provide practice and solved math questions to help you put your knowledge to the test.
What is a denominator?
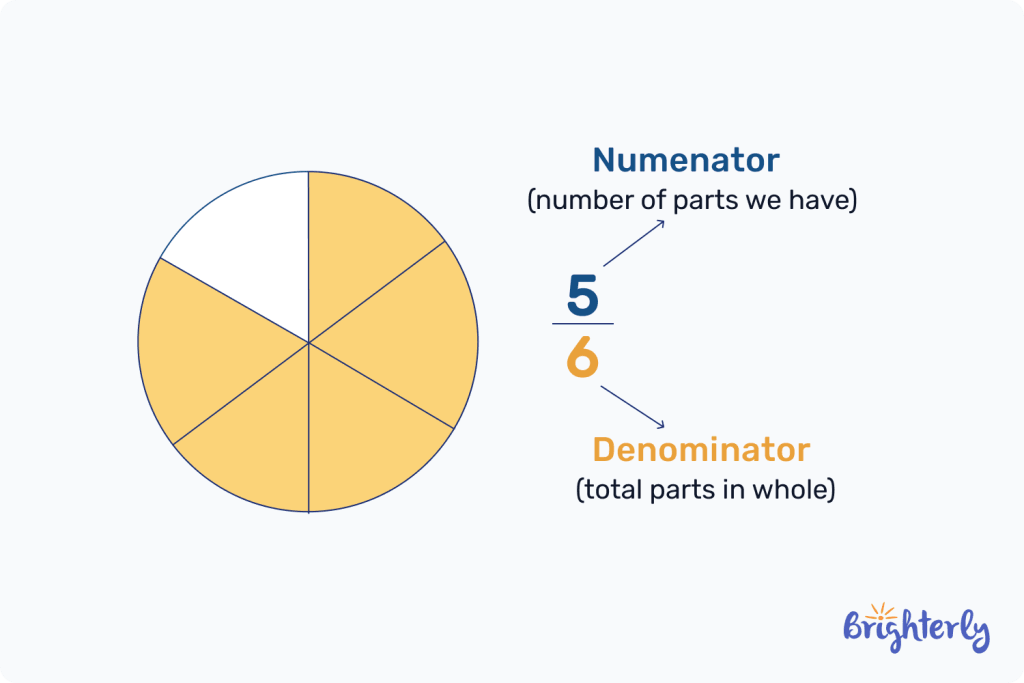
A denominator forms the bottom number in a fraction. The denominator meaning is the number below the line, and it tells us the number that is being divided into parts. For example, in ⅗, the fraction denominator of 5 is reflecting 5 parts of a whole.
The denominator is a key mathematical function when it comes to basic fraction operations, rational numbers and more, so it’s essential for kids to understand. It aids in both simple and complex mathematical calculations. Many ask, “Which one is the denominator in a fraction?” and the answer is the bottom number in a fraction.

Numerator and denominator
Once we define the denominator in math, we then need to define the numerator. The numerator represents the other part of your fraction, the top part. It represents how many parts of the whole number we have – so to use our example above, ⅗ represents 3 parts of 5 total parts.
The fraction denominator and numerator work together in a fraction to provide meaningful information about the whole. We need both in a fraction – one cannot exist without the other.
How to find the denominator of a fraction
To find the denominator of a fraction, you simply need to identify the bottom number in a fraction.
Denominator: examples
Here are some examples of fraction denominators:
| Fraction | Denominator |
| ½ | 2 |
| ¾ | 4 |
| ⅝ | 8 |
| 7/10 | 10 |
| 9/15 | 15 |
It’s also helpful to visualize fraction denominators in real-world scenarios, so here, we cover some scenarios.
| Scenario | Working out your denominator |
| Sharing a pizza | If you cut a pizza into 8 slices and take two of those slices, you’ve taken 2/8 of the pizza. Your denominator is the number of slices in the pizza. |
| A book-reading challenge | If you’re taking part in a book reading challenge, in which you need to read 10 books over the summer, and you’ve read 4 books, you’ve read 4/10. In this fraction, 10 is your target number and your denominator. |
| Saving money | If you wanted to save £100 and you’ve already saved £35, you’d have the fraction of 35/100. Here, the denominator is 100, because it is again your total target. |
Can a denominator be 0?
No, a denominator in fractions can’t be 0. This is because division by 0 is undefined in math. So we don’t have a clear way to interpret or understand a fraction where the denominator is 0. If the denominator is how many equal parts something is split into, we can’t split something into zero parts.
Types of fractions based on the denominator
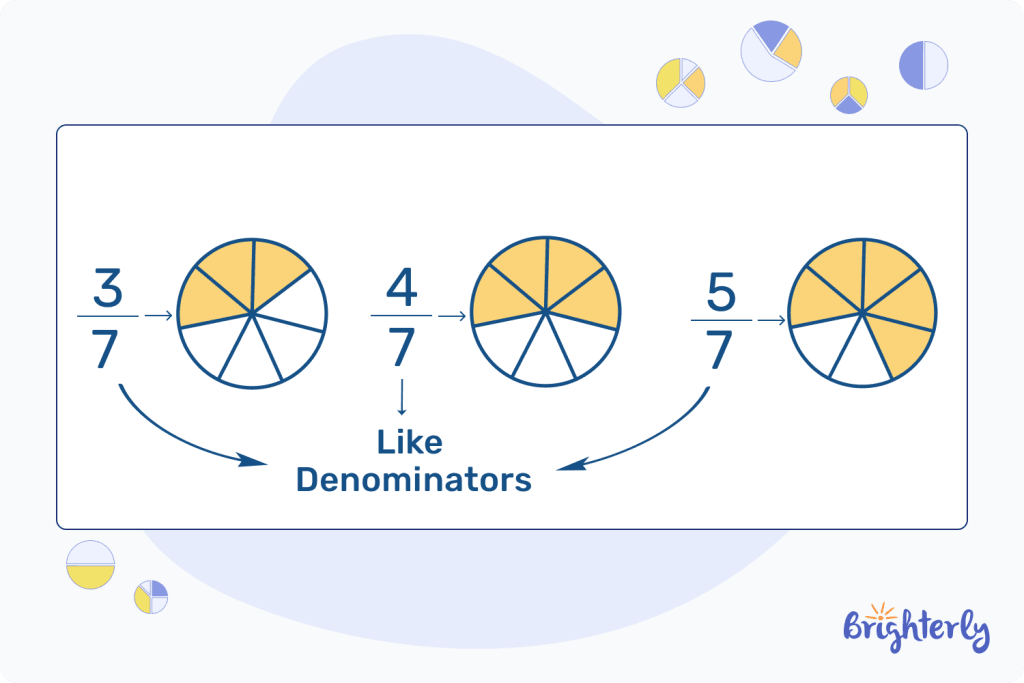
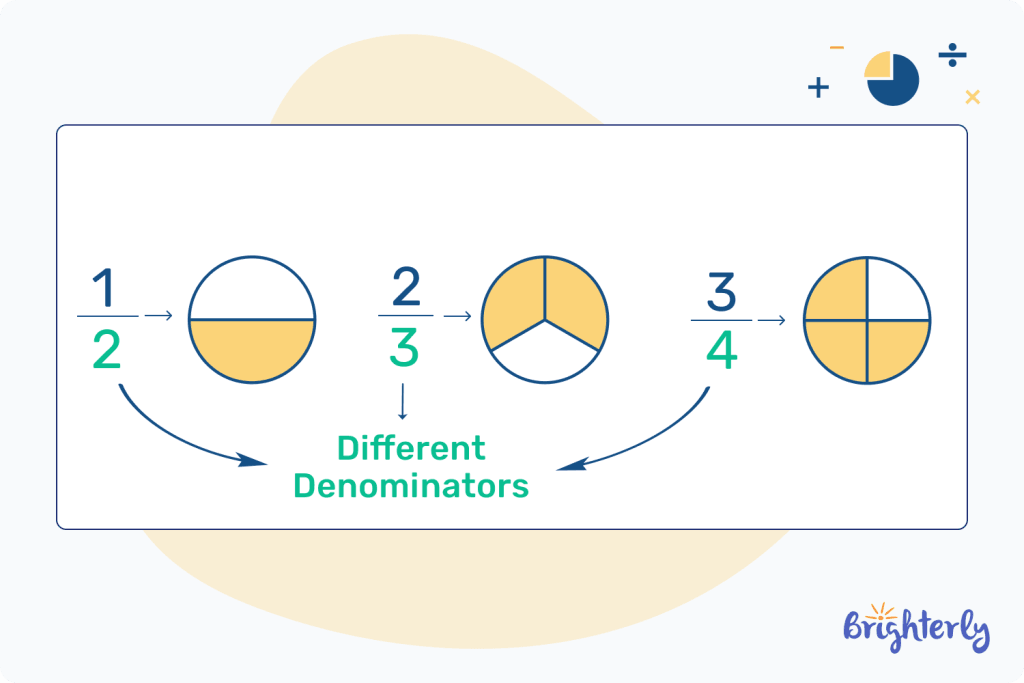
Your denominator can help you to categorize multiple fractions, too. If you have more than one fraction, you can classify them as like or unlike based on their denominator.
So, if your denominators of a fraction are all the same, like ⅕ and ⅖, they’re classed as like fractions. If your fractions have different denominators, such as ⅗ and ½, they’re classed as unlike fractions.
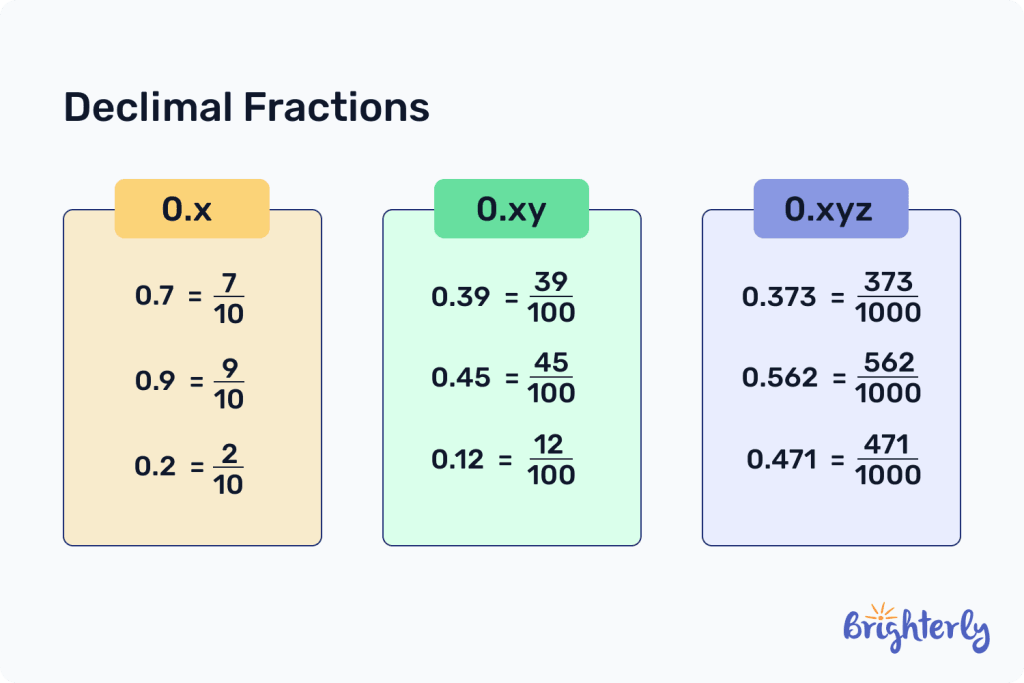
You can also have decimal fractions based on their denominator. Decimal fractions have denominators in numerals of 10 – so for example, 10, 100, 1000 – and can easily be translated into decimals. For example, 4/10 easily becomes 0.4.
Least common denominator
When it comes to working with multiple fractions in operations, like addition and subtraction, having a common denominator is essential for making them more manageable. That’s where the least common denominator (LCD), also known as the lowest common multiple, comes into play – this is the smallest number that can be evenly divided by all denominators in the set of fractions.
Let’s take the example of working with ⅗ and ½. Here, our lowest common denominator is 10, because it’s the lowest number both 5 and 2 can be divided into. The lowest common denominator makes working with fractions that have unlike denominators so much easier.

How to Find the Least Common Denominator
There’s an easy way to find the least common denominator of your fractions, but it takes a little work. You’ll need to determine the least common multiple of the denominators, and the easiest way to do that is to list the multiples of each denominator in fractions.
If we use the examples of ⅔ and ¾, you’ll list:
- Multiples of 3: 3, 6, 9, 12, 15, 18…
- Multiples of 4: 4, 8, 12, 16, 20, 24…
Then, you’ll need to identify the smallest number in both lists, which in this case is 12. You’ll find that you’ll need to list only a few multiples to find your least common multiple. But be aware that for larger numbers, you may need to list more of their multiples to find the least common multiple!
Denominator in division
The fraction denominator is also important to division, and this is especially true when you’re dividing fractions. In division, the denominator of the divisor becomes the numerator of the multiplier.
Let’s take the example of dividing ½ by ⅔. First, you’d need to multiply ½ by ⅔, which is 3/2, to get ¾.
Denominator in ratio
The denominator in the ratio represents the second term. And remember, the ratio is a comparison of two numbers by division.
Let’s take the example of the ratio 3:4. Here, 4 is the denominator of a fraction in a ratio. Ratio is important to understand concepts like proportions and rates, so it’s essential to understand the role of the fraction denominator here.
Simplifying fractions
If you’re working with large fractions, you’ll want to simplify those fractions to make them easier to work with and transform them into simpler numbers.
To do that, you need to work out the lowest common multiple of both your numerator and your denominator in a fraction.
You should list out all the numbers your fraction is divisible by first. So, let’s use the example of 16/24.
- Numbers 16 is divisible by: 1, 2, 4, 8
- Numbers 24 is divisible by: 1, 2, 3, 4, 6, 8, 12
Then, you need to identify the largest common number and divide both your numerators and denominators by it.
The largest number here that both numbers are divisible by is 8.
- 16 ÷ 8 = 2
- 24 ÷ 8 = 3
Therefore, your simplified fraction is ⅔.
Solved math tasks: examples
Here, we’ve included some solved math tasks that will help you practice your fraction denominator and fractions knowledge. Try out the tasks then check the answers to see if you’re right!
Solved math task 1
I have a snack bowl with 15 snacks in it. 5 of those snacks are chocolate bars.
Represent the chocolate bars as a fraction.
Answer:
| 5/13. |
Solved math task 2
Find the lowest common denominators of ⅝ and 11/12.
Answer:
| 15/24 and 22/24. |
To work this out, find:
- Multiples of 8: 8, 16, 24, 32, 40, 48
- Multiples of 12: 12, 24, 36, 48
The lowest common multiple of both numbers is 24, so you’d work out what you need to multiply your numbers by to get 24.
- 8 x 3 = 24. Multiply your 5 by 3: 15
- 12 x 2 = 24. Multiply your 11 by 2: 22.
Solved math task 3
Rewrite the fractions ⅙ and 1/18 as fractions with 54 as the common denominator.
Answer:
|
9/54 and 3/54. |
Divide 54 by your denominators:
- 54 ÷ 6 = 9
- 54 ÷ 18 = 3
Then, you just need to multiply your numerators by those numbers to get your equivalent fractions:
- 1 x 9 = 9
- 1 x 3 = 3
Denominator: practice math problems
Denominator worksheets
We’ve created some free math worksheets that cover fraction denominators to help you solidify your knowledge:







