Division Property of Equality – Definition With Examples
reviewed by Jo-ann Caballes
Updated on December 11, 2024
Division property of equality is one of the most crucial formulas in math that can be used anywhere: from groceries to rocket science. However, it can be tricky for many students. That’s why we’ve gathered everything you need to know about this topic, so you’ll get your answers to questions such as “Which equation requires the use of the division property of equality to be solved?”.
What Is Division Property of Equality?
The division property of equality states that if you divide both sides of an equation by the same non-zero number, the equation remains balanced or equal.
Division property of equality definition
The division property of equality definition states that if you divide both sides of an equation by the same number (if it’s not a zero), the equation will remain balanced or equal.
Division property of equality example
To better understand this topic, let’s take a closer look at some examples of the division property of equality. Let’s take a look at one of the easiest illustrations for kids in third grade:
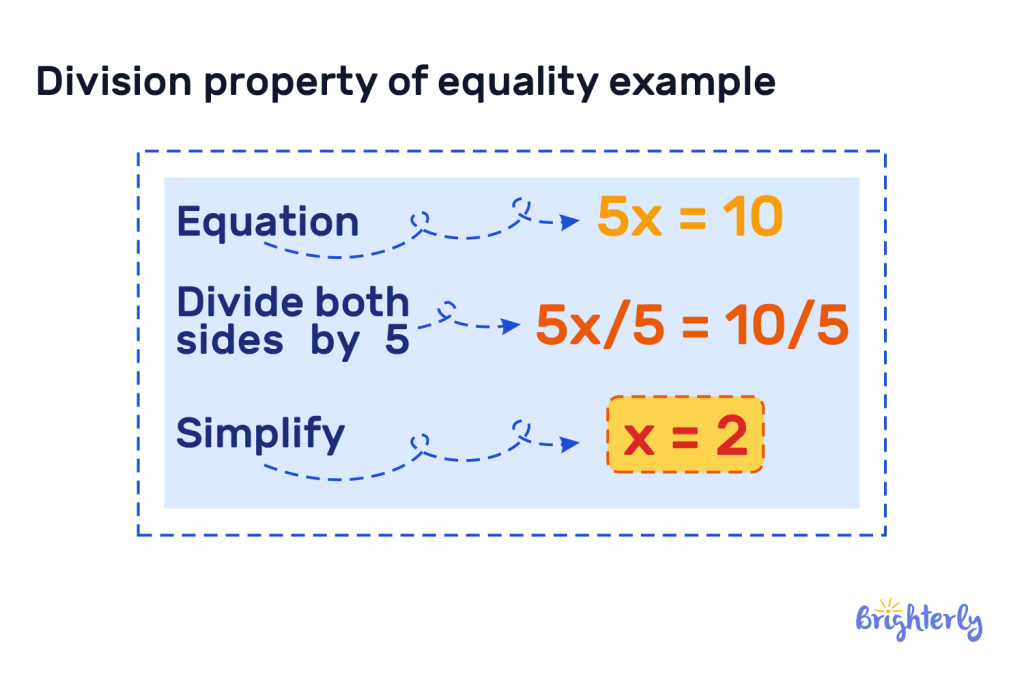
In this example of the division property of equality, we divided both sides of the equation by 5 to isolate the variable x.
The Inverse of Division Property: Multiplication Property of Equality
The multiplication property of equality states that if you multiply both sides of an equation by the same non-zero number, the equation remains balanced or equal.
Imagine a situation where 5 people get 3 apples each, and we need to determine the total amount of apples. In this situation, the equation will look the next way.
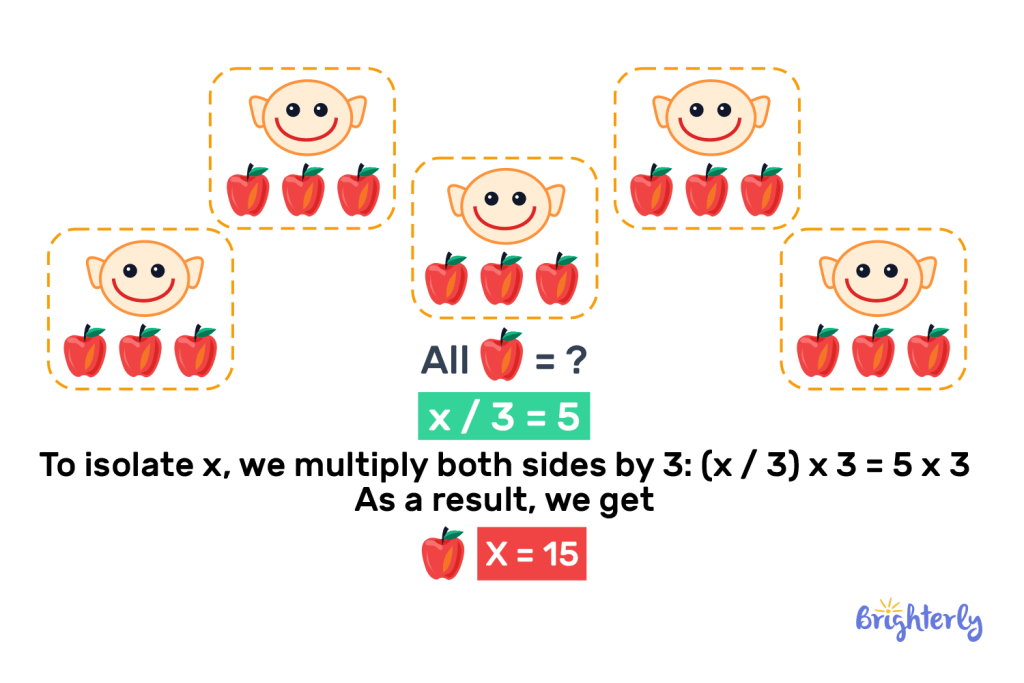
In essence, multiplication and division are inverse operations. They “undo” each other. So, while solving an example of the division property of equality, you can use multiplication.
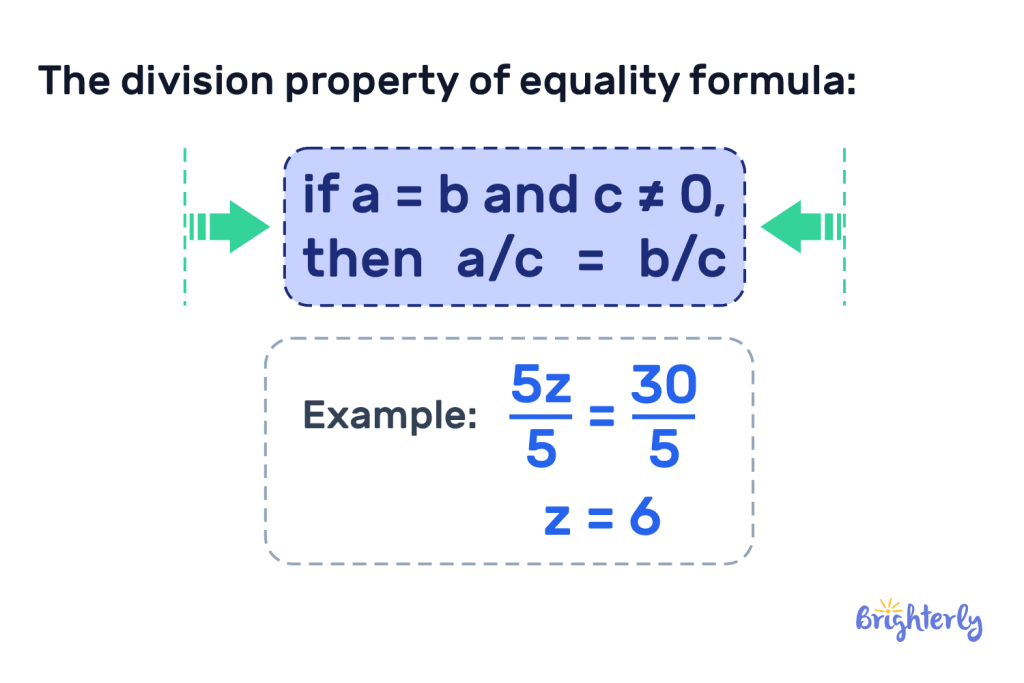
Formula of Division Property of Equality
The division property of equality formula is pretty easy and can be described in the next way: “If a = b and c ≠ 0, then a/c = b/c.”
Division Property of Equality Calculator
Luckily for students, there are dozens of division property of equality calculators that can help them in this tedious task. Moreover, modern AI-based chatbots can help solve equations, too! You can just put the equation into the chat and ask the bot to get the answer and provide you with an in-depth explanation of each step.
We still recommend double-checking AI-based answers on division property solutions, but at least they can simplify your understanding of this concept.
Division Property of Equality in Geometry
The division property of equality in geometry follows the same rules as in algebra. While working with shapes, if two lengths, areas, or volumes have some ratio, we can divide them both by the same non-zero value, and they will still have the same ratio. Those division properties aid in finding unknown values and solving complex geometrical problems.
Division Property of Equality with Fractions
Division property of equality still works even when you work with fractions. When we divide both sides of an equation by the same fraction, the equation is balanced. Numbers are different, but the ratio is the same.

What Are the 8 Properties of Equality?
There are 8 crucial properties of equality that you should know about. These are reflective, symmetric, transitive, and substitution properties and characteristics related to the math actions in the equation (addition, subtraction, multiplication, and division). Let’s examine all of them in a simple visualization:

How Is the Division Property of Equality Used?
The division property of equality is used in solving equations by isolating parts of it. You need to understand the definition of division property of equality and the concept that lies behind it to transform the equation into a simpler form. Here’s a step-by-step breakdown of how it’s used.

That’s literally all! As you see, the properties of division here are easier than you expected.
Solved Examples of Division Property of Equality
Let’s review the division property of equality examples to solidify your knowledge. Put it into practice with an example.
- Let’s find the X value in the equation: 8x = 48
All you need to do is divide both sides by 8 to get that x = 6 - Let’s find the Y value in the equation: 7y = 14
Divide both sides by 7 to get y = 2
If you want to know how to solve the division property of inequality, the general rule stays the same: if both sides are divided by the same positive number, then the sense (inequality symbol) remains the same.

Remember, the balance is the key to any equation. Let’s solidify the knowledge with the division property of inequality example:
4x ≥ 20
Identify the coefficient as the first step. The coefficient of x is 4. Divide both sides by the coefficient: 4x / 4 ≥ 20 / 4. Simplify this equation to get x ≥ 5.
Explanation: We divided both sides of the inequality by a positive number (4). When dividing by a positive number, the inequality symbol remains the same.
Practice Problems on Division Property of Equality
Problem 1: Sharing Cookies
If 4 classmates share 24 cookies, how many does each of them get?
Answer
Let’s set the X as the number of cookies per companion.

Problem 2: Dividing Candy
A teacher has 35 pens to distribute equally among 5 students. How many office supplies will each student get?
Answer
Let’s set the X as the number of pens per student. In this case,

Division Property of Equality: Practice Math Problems
Division Property of Equality: Worksheets
We know that the division property of equality is not the easiest topic for any student. That’s why we’ve gathered the best free algebra worksheets to upgrade and solidify the math skills of your child:
- Solving Equations With Variables On Both Sides Worksheets
- Algebra Equations Worksheets
- Multiplication and Division Worksheets Grade 3
Frequently Asked Questions on Division Property of Equality
What is the Division Property of Equality?
The division property of equality notes that if you have an equation and divide its parts by the same number, the equation remains balanced.
How does the Division Property of Equality work?
The division property of equality works in the way that if you divide both sides of an equation by the same number, the equation stays balanced.
Can the Division Property of Equality be used with fractions?
Yes, you can use the division property of equality with fractions as well as decimals. If you divide both parts of the equation by the same number, the equation and its ratios will stay balanced.
How is the Division Property of Equality used in real-life situations?
The division property of equality is used in various real-life situations. If you know the total cost of several items, you can use this property to calculate the cost of each item. You can determine the average speed by knowing the distance and time taken.