Common Multiples – Definition, Properties, Examples
reviewed by Jo-ann Caballes
Updated on November 12, 2024
Welcome to Brighterly, where we are no strangers to helping children navigate through the fun, yet sometimes challenging world of mathematics.
Today, we’re going to take a look at common multiples. Common multiples are numbers that we find in the multiples of two or more numbers.
Here, we cover the common multiple definition and common multiple meaning, as well as examples to simplify the concept, and finally, practice questions to help the young Einsteins master the topic that is common multiple.
What is a common multiple?
Common multiples are the numbers that appear in the multiples of two or more numbers.
Remember that multiples are the results we get when multiplying a whole number by another integer.
For example, the multiples of 2 are 2, 4, 6, 8, 10, etc.
And so are the multiples of 4: 4, 8, 12, 16, and so on.
Common multiples refer to the same multiples that occur when two or more numbers are multiplied by other integers.
Therefore, we can rightly say that the common multiples of 2 and 4 are 4, 8, 10, 12, and so on.
How to find common multiples?
To find the common multiples of two or more numbers, we start by listing out the multiples of each number.
For example, if we were to find the common multiples of 7 and 3, we would begin by listing all multiples of 7.
These are: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, and so on
Then, list all multiples of 3, i.e. until we find the number of common multiples we need. In this case, just two will suffice:
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42.
Now that we have listed the multiples of both numbers, we can specify the numbers that appear in their multiples:
These are 21 and 42.
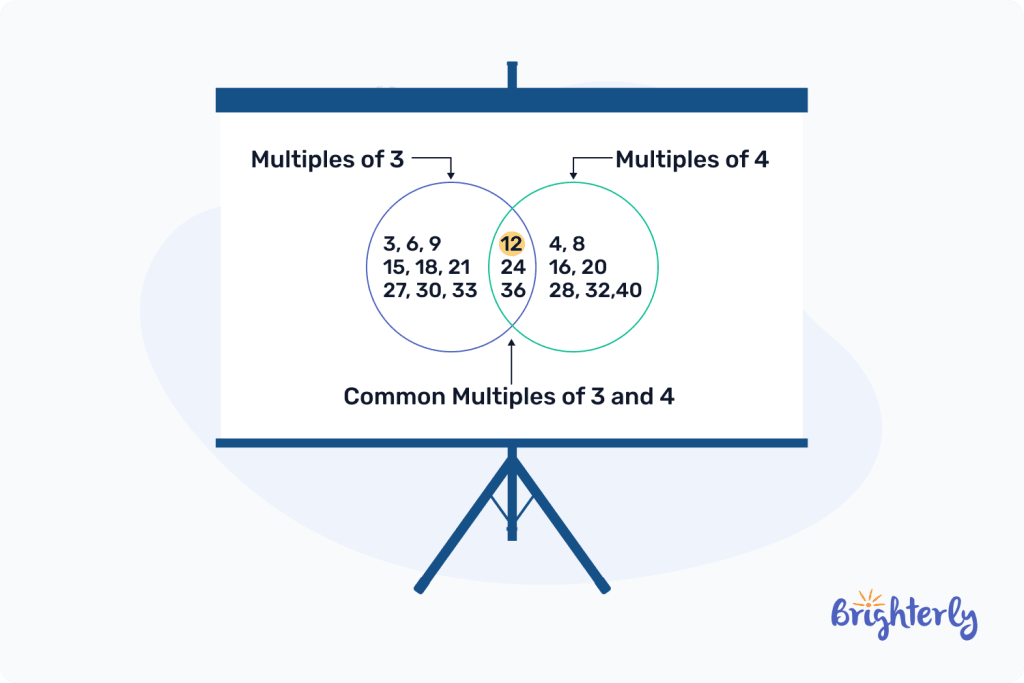
Another way we can quickly identify the same numbers that occur in the multiples of both numbers is by using a common multiple chart.
We highlight the multiples of 6 and 7 with different colors to find their multiples as in the image below:
Next, we can easily identify the common multiples as any number that has the highlight color of both multiples
Thus, the common multiples of 6 and 7 from 1 to 100 are 42 and 64 only.
However, please note that this method is not advisable for finding the common multiples of larger numbers.
Common multiple between two numbers
We can find the common multiples between two numbers simply by listing out each of the two given numbers, then writing out the multiples, and finally, identifying which numbers from the lists occur in both multiples.
For instance when finding the first common multiple of 3 and 5:
Multiples of three are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, etc.
Multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, and so on.
Therefore, the first common multiple of 3 and 5 is 15.
Note that the common multiple(s) between two numbers must be divisible by those numbers.
Common multiple between three numbers
We can also find the common multiples between three numbers and even more. All we have to do is follow the same procedure as before:
We list out the multiples of each number, then identify the multiples that occur across all the numbers, not just two of them but all.
For instance, if we were to look for the common multiples of 2, 4, and 7:
The multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, etc.
The multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, and so on.
The multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, etc.
Upon close examination, we can tell that some numbers occur in the multiples of 2 and 4 but do not occur in 7 such as 4, 8, 12, and so on. However, we cannot call these numbers the common multiples of 2, 4, and 7 because for it to be a common multiple, it has to appear in the multiples of all the numbers given.
Therefore, the common multiples of 2, 4, and 7, begin with 28, followed by any number that occurs in the multiples of the three numbers — the next is 56 by the way!
Again, remember that the common multiple of the numbers must be divisible by those numbers.
What is the least common multiple of 4 and 3?
The least common multiple (LCM) is the lowest multiple across two or more numbers.
This means we are to find the lowest number that is divisible by both 4 and 3.
We start by writing down the multiples of four which are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, and so on.
After which, we list the multiples of three: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, and so on.
Now that we know the multiples of 3 and 4, the next thing is to identify the smallest common multiple or the multiple that occurs first in both numbers which is 24.
We can also find the least common multiple of numbers with the prime factorization method where we list the prime factors that make up each number, then multiply the common factors.
Likewise, we can use the division method: we simplify each number to its lowest divisible form and multiply the factors.
Common multiple: Properties
The properties of common multiples are the unique features that are specific to common multiples:
- There are an infinite amount of common multiples between two or more integers.
- The product of two or more integers is most likely a common multiple of those integers. For instance, 6 is one of the common multiples of 3 and 2, and 2 × 3 = 6.
- When coprime numbers (numbers that are not divisible except by 1) are multiplied, the result is the common multiples of both numbers. For example, the coprime numbers 8 and 15, when multiplied give us 120, and the common multiples of 8 and 15 are the multiples of 120 which are 120, 240, 360, 480, 600, 720, and so on.
- This also means the lowest common multiple of the coprime numbers is their product result. For instance, for coprime numbers 2 and 3, the least common multiple of both numbers is their product which is 6.
Solved Math Tasks: Examples
Solved math problem 1
Answer the following questions:
- Is 16 a multiple of 4?
- What are some common multiples of 5 and 7?
Answer
1. Firstly, we multiply 4 by other whole numbers until we find 16 and the multiples of 4 are 4, 8, 12, 16, etc.
|
Therefore, 16 is a multiple of 4. |
2. The second question requires that we list multiples of 5 then the multiples of 7. The multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, and so on.
Then, the multiples of 7 which are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, and so on.
We can identify from both lists that the lowest common multiple for 5 and 7 is 35.
And as we learned above, since 5 and 7 are coprime numbers, their common multiples are the multiples of 35.
| Therefore, the multiples of 35 which are 35, 70, 105, 140, 175, 210, 245, 280, etc, also serve as the common multiples of 5 and 7. |
Solved math problem 2
What are the first five common multiples of 6 and 9?
Answer
Unlike our previous example of 5 and 7, 6 and 9 are not coprime numbers, which means we need to scan through the lists of their multiples to identify which numbers appear in both.
The multiples of 6 are 6,12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, and so on.
The multiples of 9 are 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, etc.
|
The first five common multiples are 18, 36, 54, 72, and 90. |
Solved math problem 3
What is the least common multiple (LCM) of 7 and 11?
Answer
The least common multiple is the smallest common multiple for our given numbers so again, we list out the multiples of 7 which are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, and more.
Then we look at the multiples of 11 which are 11, 22, 33, 44, 55, 66, 77, etc. We don’t need to keep going since we’ve found the first number that occurs in the multiples of both integers.
|
77 is the least common multiple of 7 and 11. |
Common multiple: Practice Math Problems
Common multiple: worksheets
Improve your child’s mastery of common multiples by engaging them with our free worksheets:
Problems with Fractions?
- Does your child struggle to master fractions?
- Try lessons with an online tutor.
Choose kid's grade
Is your child having trouble understanding the concept of fractions? An online tutor could provide the necessary support.
