Mixed Number – Definition, Example, Facts
reviewed by Jo-ann Caballes
Updated on October 28, 2024
Numbers can be expressed as whole, decimals, and fractions. We can also express numbers as mixed numbers — this type is used in representing numbers in both whole numbers and fractions.
Read on to learn more about the mixed number meaning along with examples and practice questions.
What is a mixed number?
A mixed number, also known as a mixed fraction, is used to express improper fractions by combining a whole number and a proper fraction. This combination is used to represent numbers in a more comprehensible format.
Mixed number definition
We define a mixed number as the mixture of a whole number and a proper fraction. This mixture makes numbers easier to express instead of using improper fractions. An improper fraction is a fraction type where the denominator is less than the numerator such as 3/2
Mixed number example
For the example of a mixed number, let us take the improper fraction mentioned above 3/2. If it were a mixed number, it would become 11/2.
As a mixed number fraction, it has changed from what was an improper fraction to a whole number (1) and a proper fraction (1/2 ).
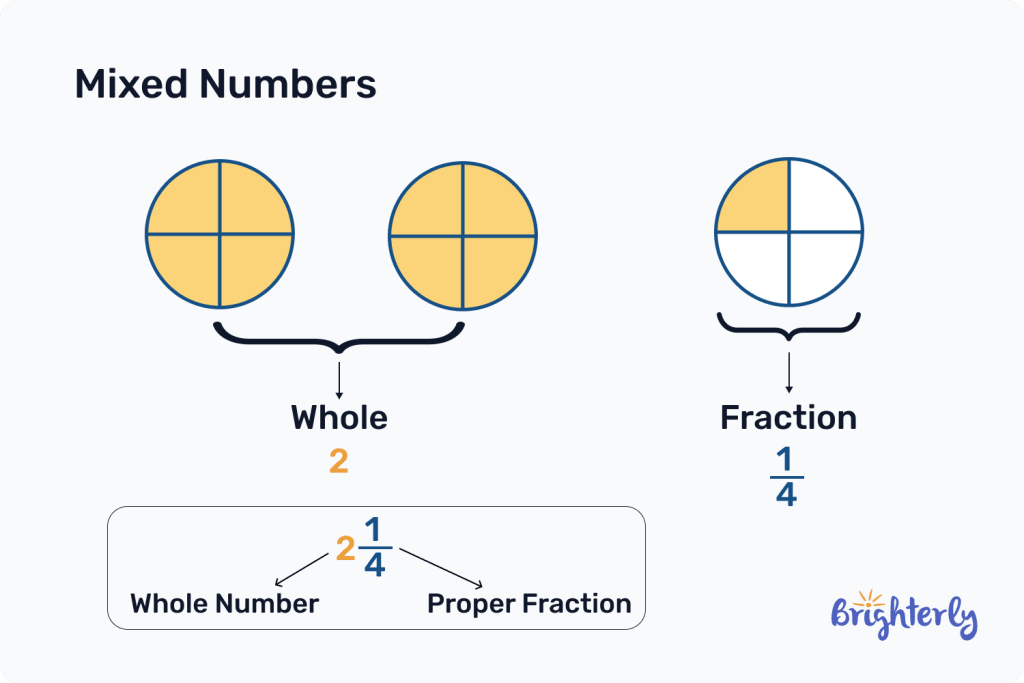
Parts of a Mixed Number
The parts that make up a mixed number can be broken down into three:
- Whole number
- The numerator (the number on the top of the fraction)
- The denominator (the number at the bottom of the fraction)
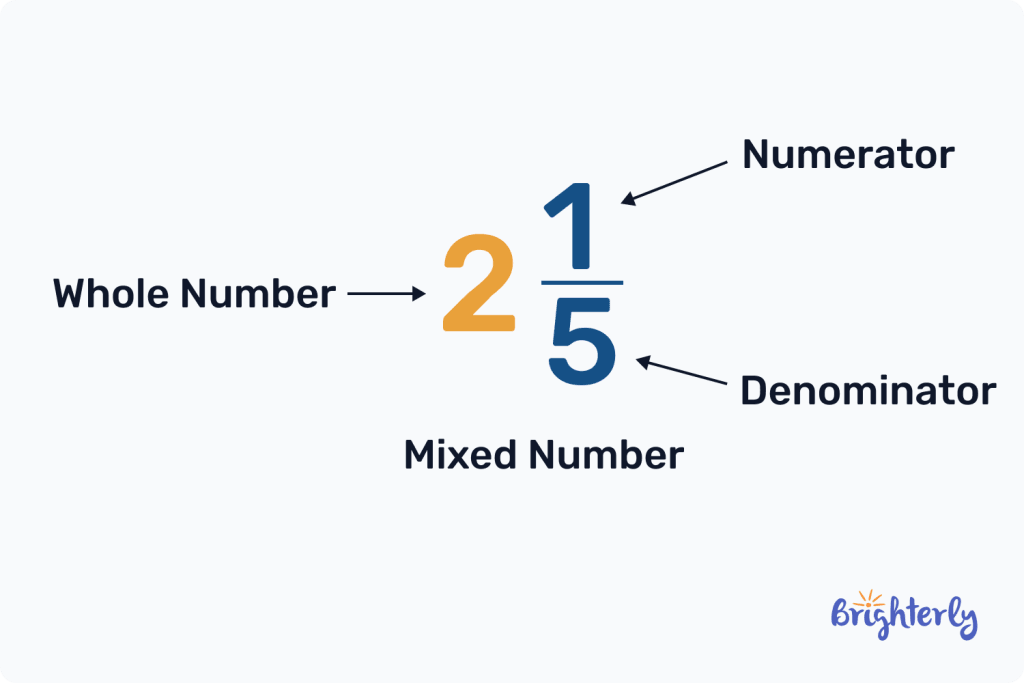
The numerator and denominator make up a part of the whole number. If we had 5/5 as our fraction that would be a complete whole number (1) because the numerator and denominator are the same.
With mixed number fractions, we can show whole numbers and their fractional remainder. This helps us understand that the denominator is the amount needed for a number to become a whole.
For instance, if John was given 11/2 of a cake, this means the cake can be divided into 2 parts, and if John was given 1 part and half, it also means only 1/2 of the cake is left.
Properties of Mixed Numbers
The following properties are the qualifying ingredients that determine a mixed number:
- It has three parts (whole number, numerator, and denominator), or two parts if you like (whole number and proper fraction)
- It can be converted to and from an improper fraction
- It must be greater than 1
What is a mixed fraction?
A mixed fraction is the same as a mixed number – the mixture of a whole number and a proper fraction.
We used mixed fractions instead of improper fractions because they are more convenient for representing numbers that are not up to another whole number. For instance, it is easier to understand that 13/4 is close to 2 but we can’t say the same about 7/4.
How to convert improper fractions and mixed numbers?
Improper fractions can be changed to mixed numbers and vice versa, let’s first go over how to change improper fractions to mixed numbers using 7/4:
Step 1: We divide the numerator by the denominator, i.e., the number at the top by the number at the bottom: 7 ÷ 4 = 1 quotient and a remainder of 3. This is because 4 can be found in 7 once (1) and what is left is 3.
Step 2: The quotient (1) is then converted to the whole number and the remainder becomes our numerator.
Step 3: The denominator remains the same, which means the mixed number is 13/4.
Using 13/4, here’s how to convert mixed numbers to improper fractions:
Step 1: We multiply the denominator by the whole number: 4 × 1 = 4
Step 2: We sum the product with the numerator: 4 + 3 = 7, and this becomes our new numerator.
Step 3: Once again, the denominator remains the same, making 7/4 the improper fraction.
Adding and subtracting mixed numbers
Mixed numbers can be added, subtracted, and even multiplied. However, they need to be converted to improper fractions first. Here are the ways to calculate mixed numbers:
Adding mixed numbers
After the mixed number has been converted to an improper fraction, we would then sum the two numerators only. For example, if we were to add 32/3 and 61/3, we would convert them to improper fractions which is 11/3 +19/3 = 30/3 = 10.
Subtracting mixed numbers
The same method applies to the subtraction of mixed numbers. If we were to subtract 73/6 – 39/6, we would first convert them to improper fractions: 39/6 – 27/6 = 12/6 = 2.
Note: If the numbers do not share a common denominator, you will find the lowest common multiple of both denominators and use it as your new denominator after calculation.
Mixed Numbers: Real Life Examples
Mixed numbers examples can be found in most places in the real world if you pay close attention. Below are some examples:
- One and a half of a cake can be expressed as 11/2
- Two-quarters of a gallon of water is a mixed fraction of 23/4
- If the time is 2:30, it can be 21/2 or 22/4 when converted to a mixed fraction.
Solved Math Tasks: Examples
Solved math problem 1
Express this as a mixed number:
A pizza has 8 slices, Jimmy eats 2 and a half, and Mark eats 2, how many are left?
Answer
8 – 41/2 = 31/2
| There are three and a half slices of pizza left. |
Solved math problem 2
Convert the mixed fraction 122/5 to an improper fraction.
Answer
Following the steps we discussed above, we’d convert the given numbers thus:
5 × 12 + 2 = 62
| = 62/5. |
Solved math problem 3
What is the improper fraction 53/14 when converted to a mixed number?
Answer
53 ÷ 14 = 3 with a remainder of 11
| = 311/14 |
Mixed Number: Practice Math Problems
Mixed Number: worksheets
In this article, we have explained what is a mixed number, examples, and more, yet you can further your child’s learning about mixed numbers and fractions with Brighterly’s free worksheets:
- Mixed numbers worksheets
- Converting mixed numbers to improper fractions worksheets
- Improper fractions to mixed numbers worksheets
Struggling with Numbers?
- Is your child having difficulties with grasping numbers lessons?
- An online tutor could provide the necessary help.
Choose kid's grade
Does your child need additional support with understanding numbers concepts? Start lessons with an online tutor.
