• Math tutors
• /
• Knowledge Base
• /
• Obtuse Triangle – Definition with Examples

Obtuse Triangle – Definition with Examples

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on October 7, 2024

Every triangle must have a cumulated angle of 180° degrees. This is the same for an obtuse triangle. However, for the obtuse triangle, there are more degrees on a single angle than the rest. 

Keep reading to learn more about the obtuse triangle math definition, examples of an obtuse angle, and practice questions.

What is an obtuse triangle?

An obtuse triangle is a triangle that has one “obtuse” interior angle with a degree of more than 90°. This interior angle measures more than the other two angles, giving the triangle an obtuse shape. However, when added with the other 2 angles, the total angle of an obtuse triangle remains 180°.

Math tutors

Improve your child’s math skill today with Brighterly

Let them be at the top of their class.

Book free lesson

Which triangle is obtuse?

The obtuse triangle angle is the interior angle that measures more than 90° degrees, but less than 180° degrees. The other two angles are less than 90° degrees when combined  However, the obtuse angle, when added with the other two angles, is 180° degrees. 

To identify the obtuse angle in a triangle, look out for the longest side, then check the angle that is opposite – that’s the obtuse angle.

What does an obtuse triangle look like?

An obtuse triangle looks like a normal triangle except that one angle has a higher measurement than 90°,  which makes the other angles less than 90°when added.

It is identifiable because one side of the triangle is visibly longer than the other. This side is the opposite of the obtuse angle.

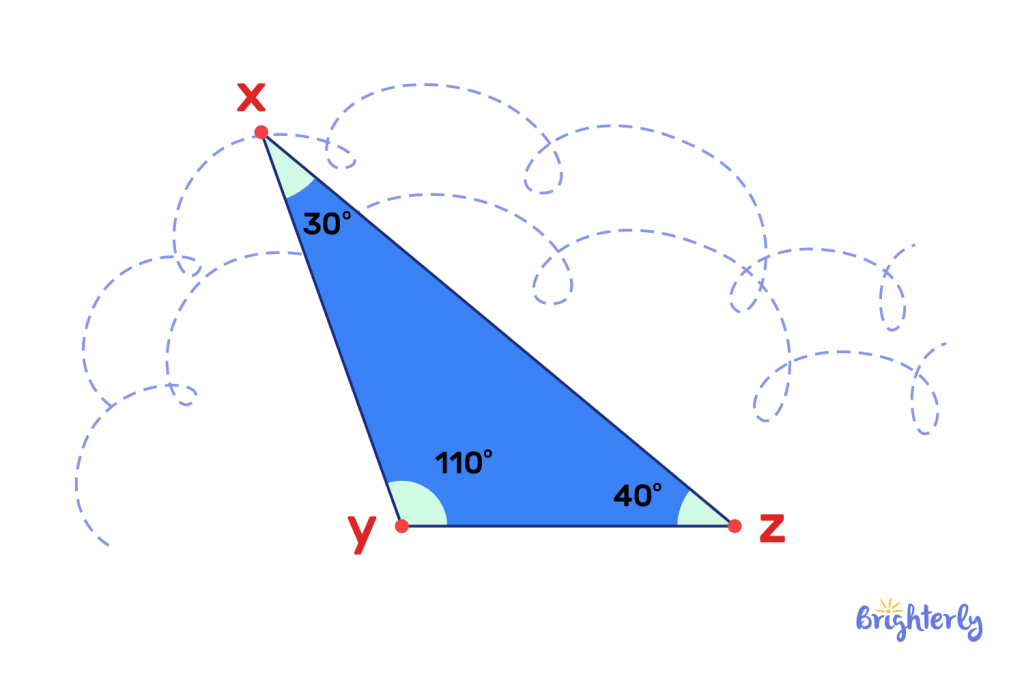
What does an obtuse scalene triangle look like?

There are two types of an obtuse triangle:

• Scalene triangle 
• Isosceles triangle

The Obtuse scalene triangle is unequal at all angles. The obtuse angle remains the largest by measuring more than 900 degrees but the other angles do not maintain the same angle degrees.

For instance, in an obtuse scalene triangle, the obtuse angle may be 1100 degrees and the other smaller angles may be 40° and 30° respectively.

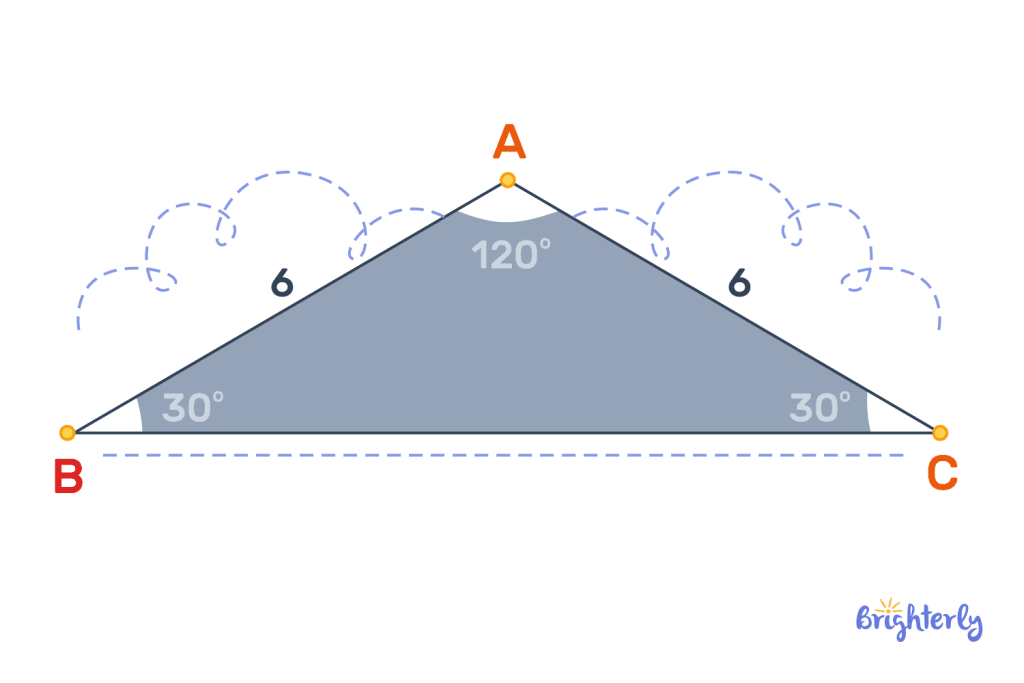
The Isosceles triangle, however, has the obtuse angle with the largest degree, and two angles with the same degree measurements.

For instance, in an obtuse isosceles triangle, the obtuse angle may be 1100 degrees and the other acute angles may be 35° and 35° respectively.

How many angles are in an obtuse triangle?

The obtuse triangle also has just 3 angles like all other triangles. However, the obtuse triangle has no right angle but has 2 acute angles (i.e., angles with less than 90° degrees) and an obtuse angle.

Examples of obtuse triangles

Let’s consider pizza! If a pizza slice is cut into a large triangular slice, the tip can be an obtuse angle with the bottom part as the largest side. Here are some other examples of an obtuse triangle in real life: 

• A cloth hanger: The obtuse angle is at the top where the hook is located
• An open book: If you open a book by the right amount, it will form an obtuse triangle, with the obtuse angle as the point where the two pages meet.

Look at your surroundings, what other examples of obtuse triangles do you see?

What types of triangles can have an obtuse angle?

As we have covered above, the isosceles triangle and the scalene triangle are the two types of triangles that can have an obtuse angle. 

The scalene triangle has unequal angles in every corner and the isosceles triangle has two acute angles and one with a larger measurement.

What shapes have obtuse angles?

Obtuse angles are not unique to triangles alone. You can find obtuse angles in any of these other polygons:

• Trapezoids
• Parallelogram
• Rhombus
• Pentagons
• Rhombus, and so on.

For each of these shapes, the obtuse angle may be different, for instance, a parallelogram with an obtuse angle will have the angle on two sides since it is a quadrilateral shape.

An example of an obtuse-angled parallelogram is a slanted rectangular window.

Solved Math Tasks: Examples

Solved math problem 1

Which of the following are characteristics of a triangle that has one obtuse angle:

1. The triangle has three equal sides. 
2. The triangle has a right-angle
3. The triangle has an angle greater than 90° degrees and two equal angles 

Answer

Note that an obtuse triangle cannot have a right angle because the obtuse angle is larger than 90° degrees.

Solved math problem 2 

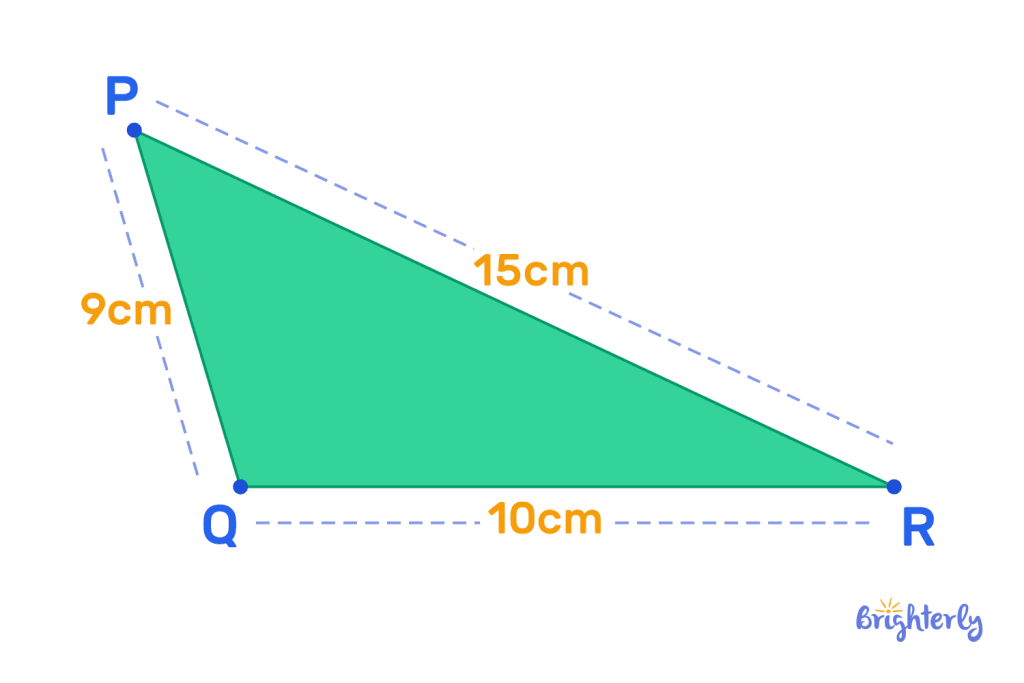
What type of obtuse triangle is this?

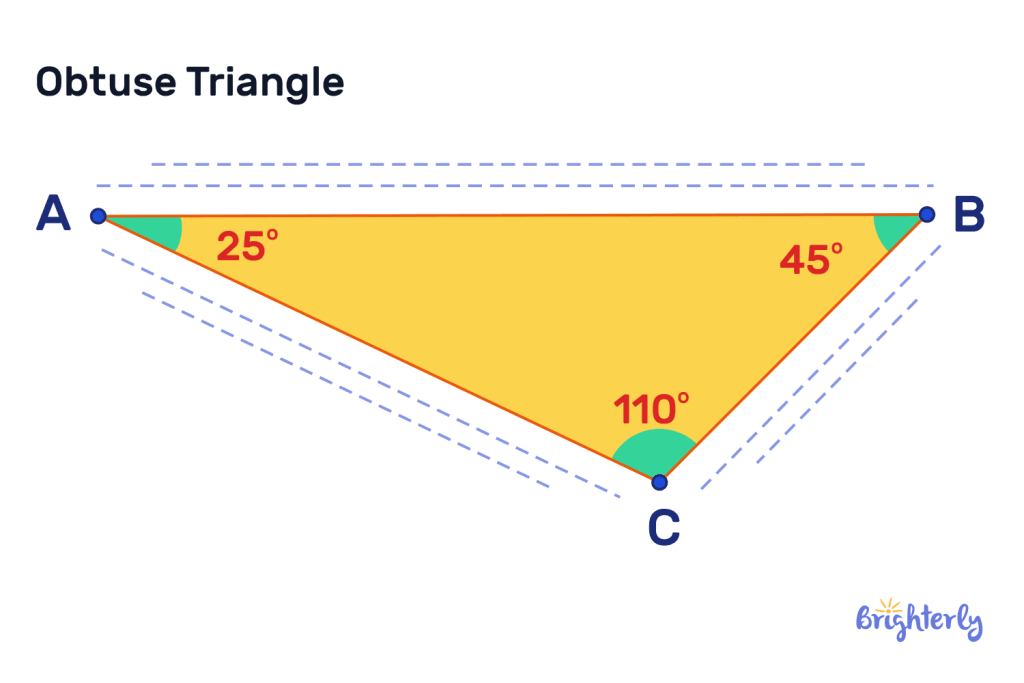
Answer

Solved math problem 3

How would you define an obtuse triangle?

1. A triangle where all the angles are greater than 90° 
2. A triangle with one angle of 90° and one obtuse angle
3. A triangle  with two angles of 90° and above

Answer

An obtuse triangle: Practice Math Problems

Obtuse Triangle: worksheets

Learn more about the obtuse angle in geometry, as well as other cool shapes with Brighterly’s free worksheets:

• Area of parallelogram worksheet
• Missing angles in a triangle worksheet
• Area of a Triangle worksheet
• Trigonometry worksheet

Jessica Kaminski

72 articles

Jessica is a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.