• Math tutors
• /
• Knowledge Base
• /
• Partial Product

Partial Product

Jessica Kaminski

Updated on December 11, 2024

Multiplication is a major arithmetic property but solving it isn’t always an easy process, especially for young learners. 

This is where the partial product method comes in. It involves splitting large numbers into smaller parts and then summing the answer. The result is the same as doing the multiplication directly. The difference is that multiplication is easier when beginners multiply using partial products.

Let’s learn more about the partial products definition and 5th-grade partial products with Brighterly

What is a Partial Product?

We know that a product is the multiplication of two or more numbers and partial means a section or part of something.

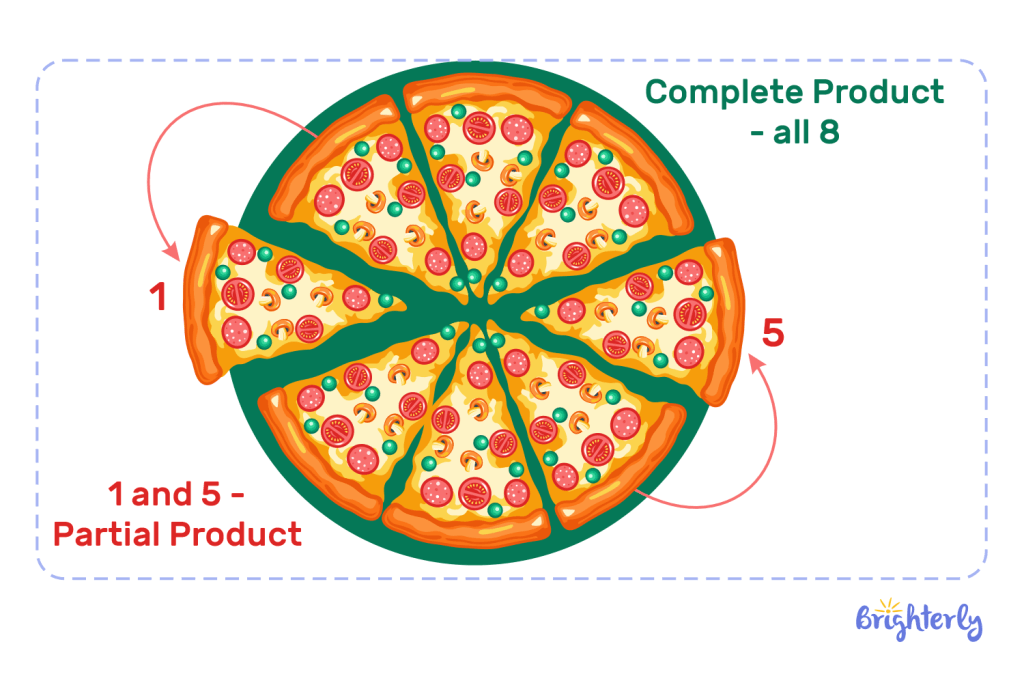
This means we can conclude that the partial products meaning is the multiplication of parts of a given set of numbers.

Partial Product Definition

Partial product can be defined as a method of solving multiplication problems by breaking down the numbers into parts and then multiplying these parts individually. After we get the “partial products”, we add them together to get the final answer. 

Partial products examples

Let’s look at some examples of partial products.

For instance, if we were to multiply 4 by 42, here’s how we can use the partial product method to solve the problem:

First, we break the number 42 into 40 + 2 and then multiply each part by 4.

40 x 4 + 2 x 4

= 160 + 8

= 168.

Please remember that the multiplication partial products method is only applicable for solving multiplication problems involving numbers greater than 10. 

Distributive Property of Multiplication

The distributive property of multiplication is the mathematical property that states that for three numbers (a, b, c), the product result of a by b and a by c is equal to the product of a by b plus c:

a x (b + c) = a x b + a x c 

Partial product multiplication

The partial products method is based on the distributive property of multiplication. 

Product of Two Numbers Using the Partial Product Method

Remember, as stated above, the partial product only applies when it includes numbers greater than 10. 

This can be the multiplication of a two-digit number with a one-digit number or the multiplication of a two-digit number with a two-digit number.

Multiplication of a Two-Digit Number with a One-Digit Number

This is multiplying a number less than 10 by a number greater than 10.

A partial product example is multiplying the 1-digit number 6 by the 2-digit number 53:

We follow the distributive property to expand and solve for the answer, so, 53 becomes 50 + 3, and the new equation is:

6 x (50 + 3) = 6 x 50 + 6 x 3

300 + 18 = 318

6 x 53 = 318.

Multiplication of a Two-Digit Number with a Two-Digit Number

Here, we multiply two numbers that are both greater than 10. For instance, let’s multiply 14 by 82.

We still use the distributive property, except with little tweaks:

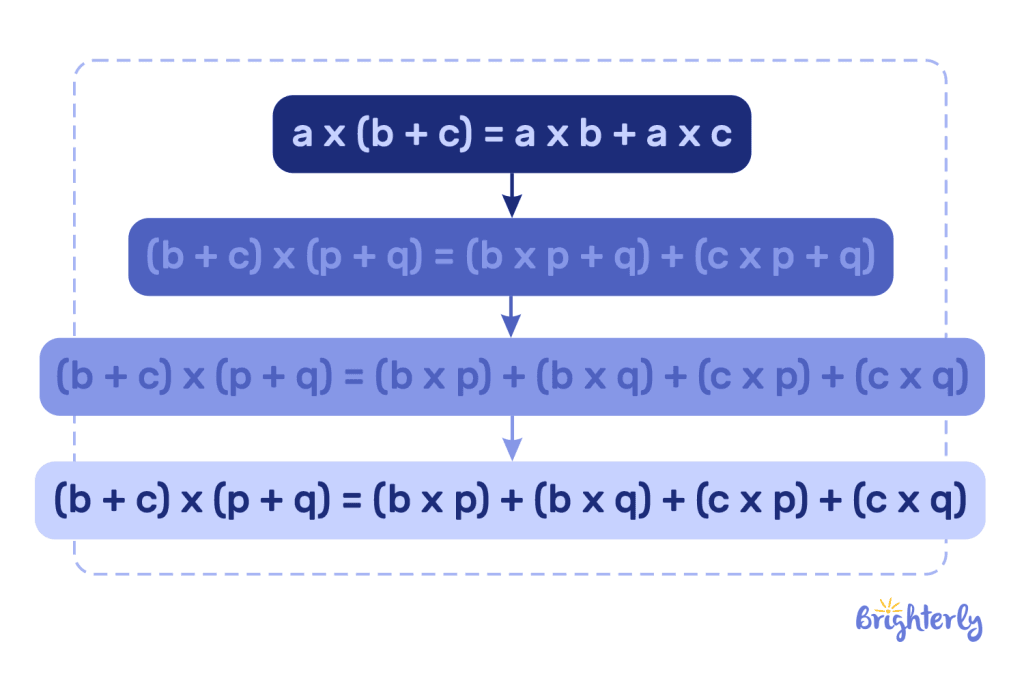
The original property is a x (b + c) = a x b + a x c. 

However, when solving for two 2-digit numbers, we replace “a” with (p + q). This means the formula becomes:

 (b + c) x (p + q) = (b x p + q) + (c x p + q)

We can further expand using the distributive property to:

(b + c) x (p + q) = (b x p) + (b x q) + (c x p) + (c x q)

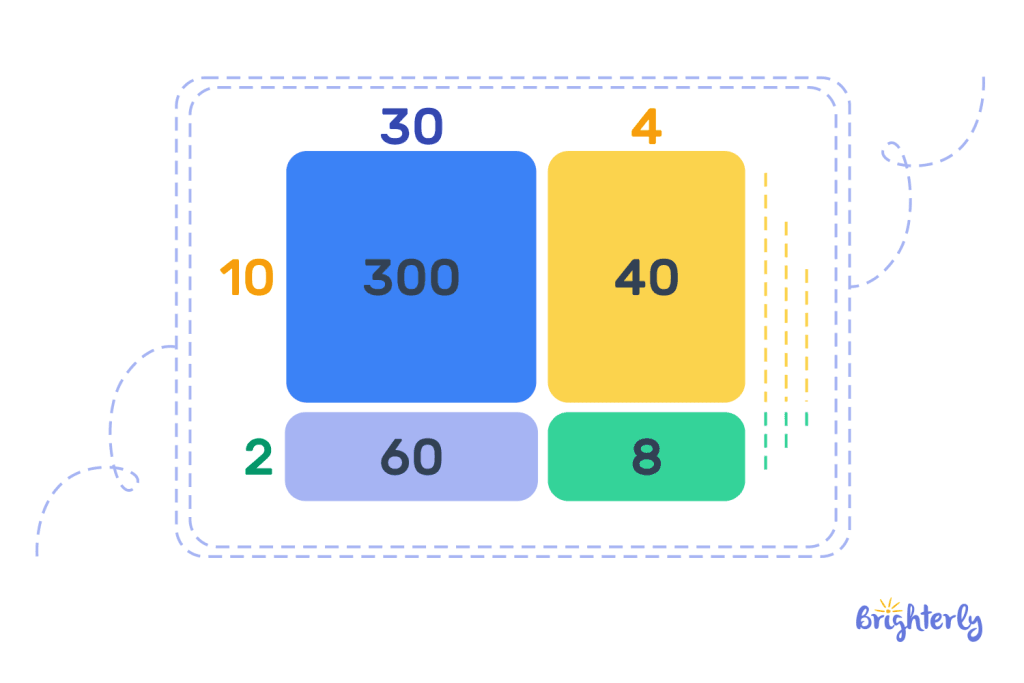
Therefore, 14 x 82 can be solved thus:

(10 + 4) x (80 + 2) =  (10 x 80) + (10 x 2) + (4 x 80) + (4 x 2).

= 800 + 20 + 320 + 8

14 x 82 = 1,148.

The formula is:

You may wonder “Why is one partial product always greater?” such as how 800 is greater than 8. The reason is because the greater part of the numbers (10 and 80) are contained in that section.

Partial Products Division

Partial products in math are not unique to solving multiplication problems alone. We can also use it to solve problems relating to division. First, we break the large numbers into partials and then add the result.

Math tutors

Join Brighterly for personalized lessons for your child

Meet the best tutors for interactive math learning.

Book free lesson

Solved Examples of Partial Product

Solved math problem 1

Using the partial product, solve 35 x  5.

Solution

30 x 5 +  5 x 5

150 + 25

Solved math problem 2

With the partial products method, multiply 52 by 13.

Solution

First, we expand:

(50 +  2) x (10 + 3) = (50 x10) + (50 x 3) + (2 x 10) + (2 x 3)

= 500 + 150 + 20 + 6

Solved math problem 3

Using the partial products method, solve the equation: 34 x 16.

Solution

(30 + 4) x (10 + 6) = (30 x 10) + (30 x 6) + (4 x 10) + (4 x 6)

= (300) + (180) + (40) + (24)

= 544.

Practice Problems on Partial Product

Conclusion

The Partial product is a mathematical method for solving multiplication and division problems. 

By simplifying before solving, complex multiplication problems can be solved more easily with the partial product method. The expert tutors at Brighterly teach this topic and other math concepts as well. Check us out!

Frequently Asked Questions on Partial Product

What is a partial product in multiplication?

The partial product in multiplication is a method of finding the product of one or two 2-digit numbers by expanding the numbers before multiplication and then summing the product result.

How do you find the partial product?

We may find the partial product by breaking down large numbers into smaller numbers, then multiplying the smaller parts, and finally adding the results.

What is the partial products calculator?

The partial products calculator is an online automation tool that helps the user find the partial products of multiplication problems without manually solving the equations. The partial products calculator is available for use on websites online.

Why is the partial products method useful?

The partial products method helps us break down complex multiplication problems into simpler steps. This can prove useful for math beginners to understand how multiplication works with large numbers by multiplying using partial products.

Jessica Kaminski

72 articles

Jessica is a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.