Perpendicular Lines – Definition, Symbol, Properties, Examples
reviewed by Jo-ann Caballes
Updated on October 3, 2024
Here at Brighterly, we’re committed to ensuring all kids have the chance to excel in mathematics with our informative articles.
Today, we’re covering the geometry concept of perpendicular lines. This concept is essential to mathematics and geometry, as well as engineering, architecture and many other disciplines.
In this article, we’ll cover the perpendicular definition and the symbol of perpendicular lines, share perpendicular lines examples and provide practice questions so you can test yourself.
What does perpendicular mean?
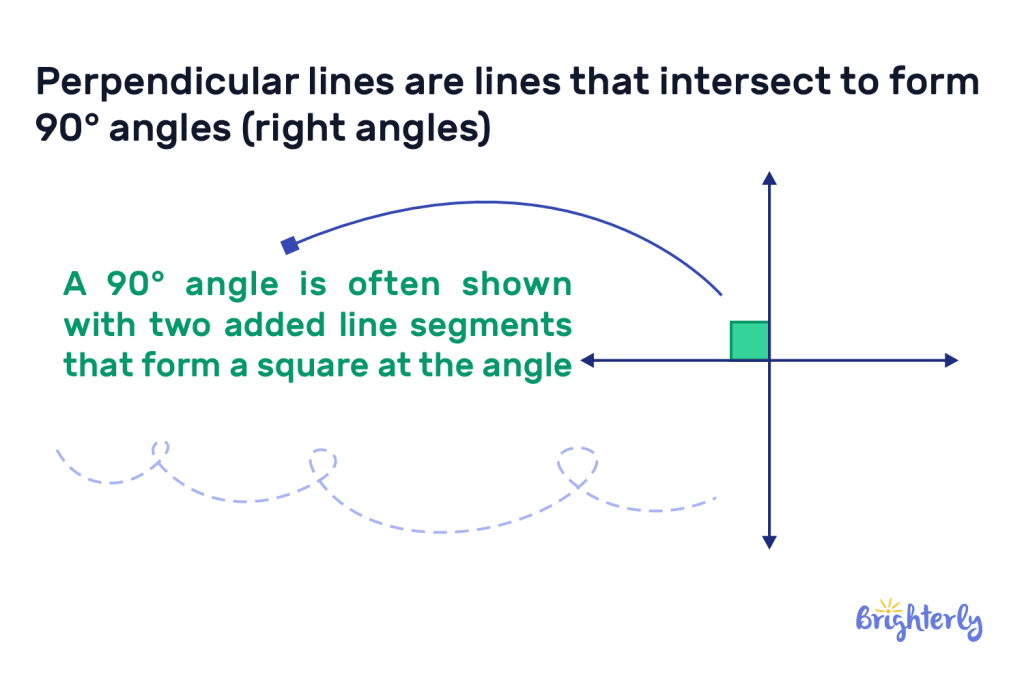
The perpendicular meaning is a 90° angle (aka a right angle) that is created as the result of two lines, planes or vectors intersecting. The perpendicular line and perpendicularity are essential concepts when it comes to mastering trigonometry, geometry, calculus and other key math disciplines.
Now you know the perpendicular meaning in math. Below, we fully define perpendicular lines and what makes them different from other line types, such as parallel lines.
Perpendicular lines: definition
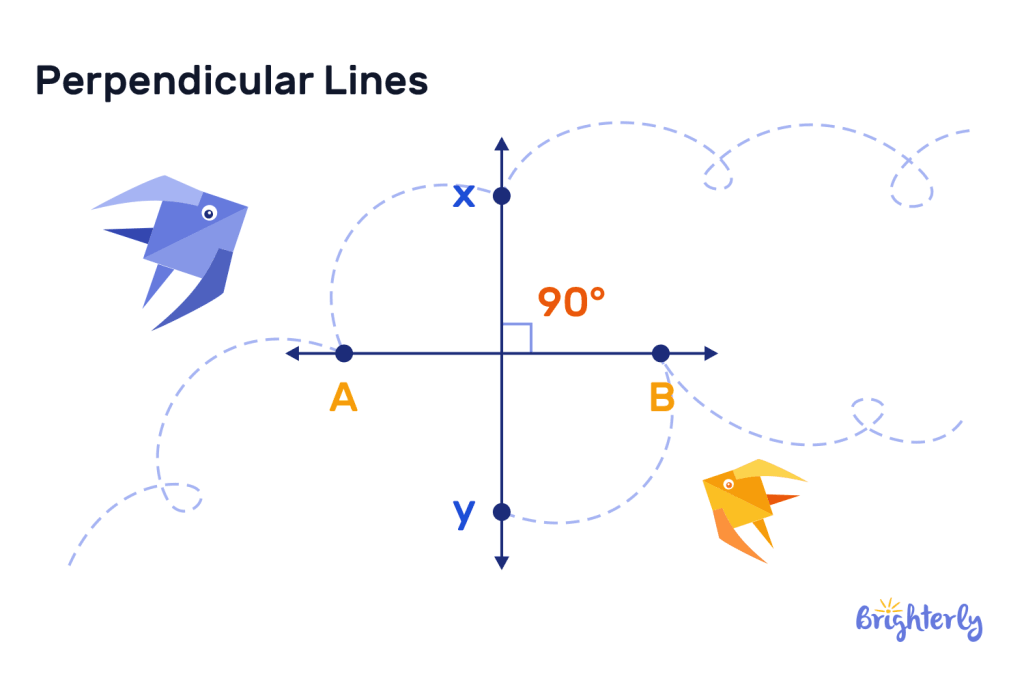
The perpendicular lines definition is two lines that intersect with one another, creating a right angle (an angle that is 90°). One perpendicular line is a line that intersects another perpendicular line at a right angle, meaning they are perpendicular to one another. Perpendicular lines essentially cross paths with one another at a specific angle that then creates a right angle.
The definition of perpendicular lines informs many different math concepts, plus their properties make many different types of problem solving easy. That’s because you can quickly and easily understand if two lines are perpendicular, often just by looking at them. If you can’t tell by looking, you can use a protractor.
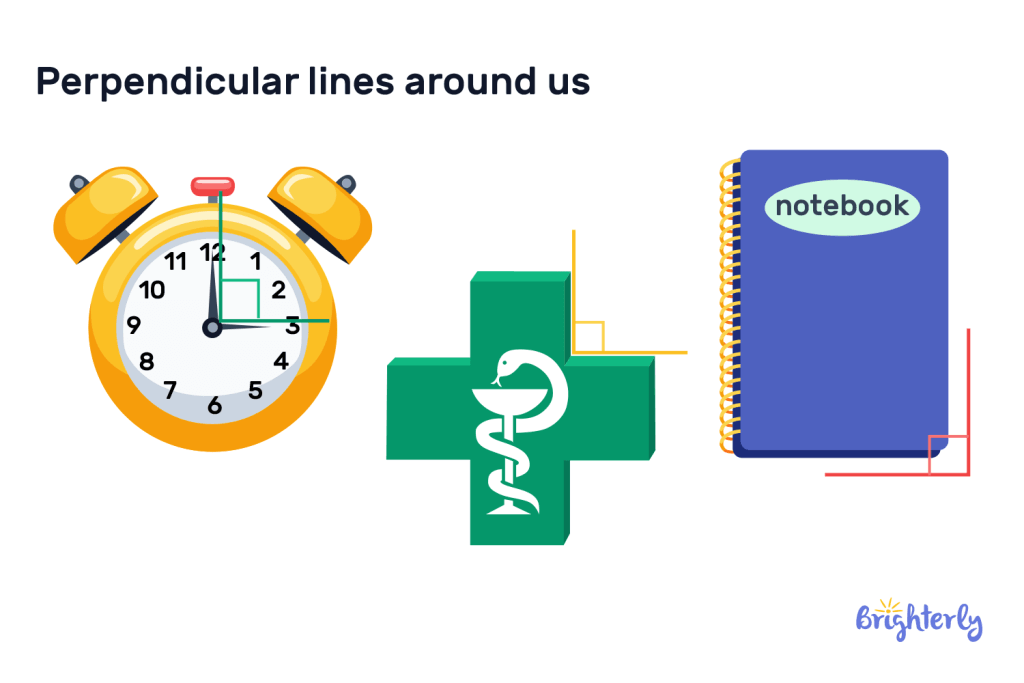
Perpendicular lines around us: examples
Perpendicular lines can be found all around us in everyday life. Here are just a few of the perpendicular lines examples you’ll see around you in real life:
- Protractor triangles – which you’ll likely use in your math learning!
- On a clock, when it hits a time that causes the arms to form a right angle
- The corners of a blackboard or whiteboard in school
- Plus signs
- The corners of windows and windowsills
- The corners of books, TVs or game consoles
- The screen of a computer or laptop
- The edges of a sports field, like a soccer field or tennis court
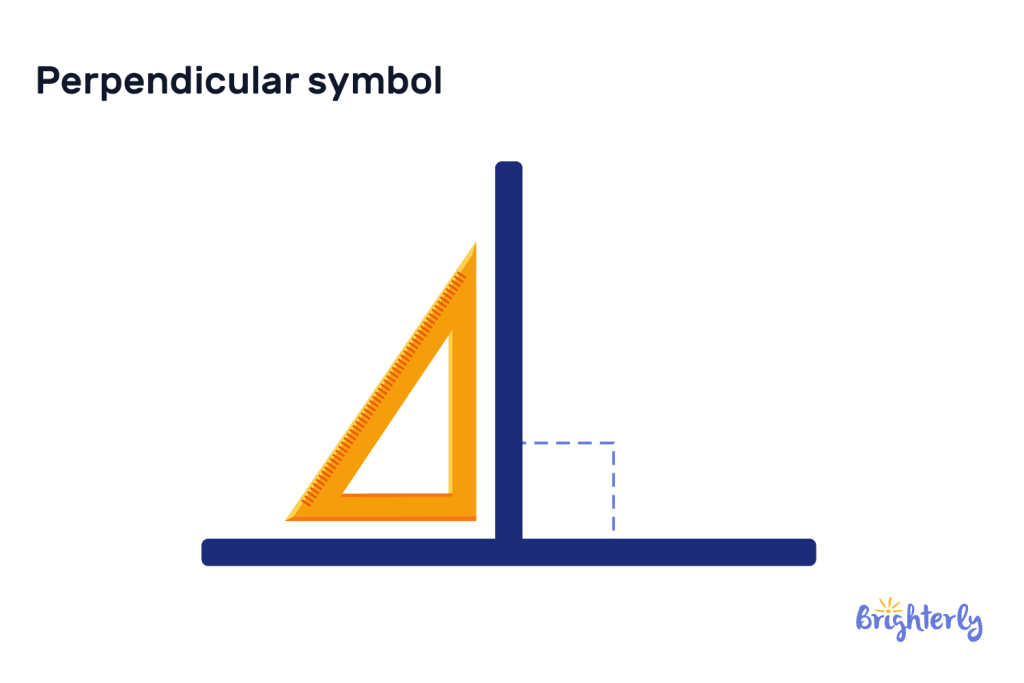
Perpendicular symbol
The perpendicular symbol is ⊥. This symbol represents a set of perpendicular lines. If we want to express this more comprehensively, we could say that ‘m’ and ‘n’ are two lines that intersect one another at right angles, therefore they are perpendicular to one another. They can therefore be represented with the expression m⊥n. The symbol is displayed this way to show the point at which the two perpendicular lines intersect as the “foot of the perpendicular”.
Generally, the standard phrase used to represent to represent two perpendicular lines is AB ⊥ CD. In this iteration, it shows that the AB line is perpendicular to the BC line.
Properties of perpendicular lines
Perpendicular lines have unique properties that make them stand out from other geometrical and mathematical rules. Not all lines that meet at an angle are perpendicular. But if they meet the criteria below, they are considered perpendicular:
- Perpendicular lines will only ever create right angles – if two intersecting lines meet and create angles that are not 90°, they are not perpendicular
- If two lines are perpendicular to the same line, they cannot be perpendicular to one another because they cannot intersect – these lines are parallel
Now you know both the perpendicular lines definition geometry and the unique properties of perpendicular lines.
The slope of perpendicular lines
There are specific rules that dictate the slopes of perpendicular lines. They are opposite and reciprocal to one another. If you need to find the slope of the line perpendicular to an equation, you’ll need to find the opposite reciprocal.
All perpendicular lines will be the inverse of the original line’s slope. You can calculate this slope by transforming a linear equation into slope-intercept form. Equally, by taking its negative reciprocal, you can also calculate the slope of a perpendicular line.
If your line has a positive slope, its perpendicular line should have a negative slope. That’s because it is the “negative reciprocal” of your positive line’s slope.
While it might seem complex to find the slope of a perpendicular line, it’s actually straightforward with this technique: if two lines have slopes m1 and m2. They are perpendicular if m1× m2 = -1. The minus sign denotes the right angle formed by the two lines.
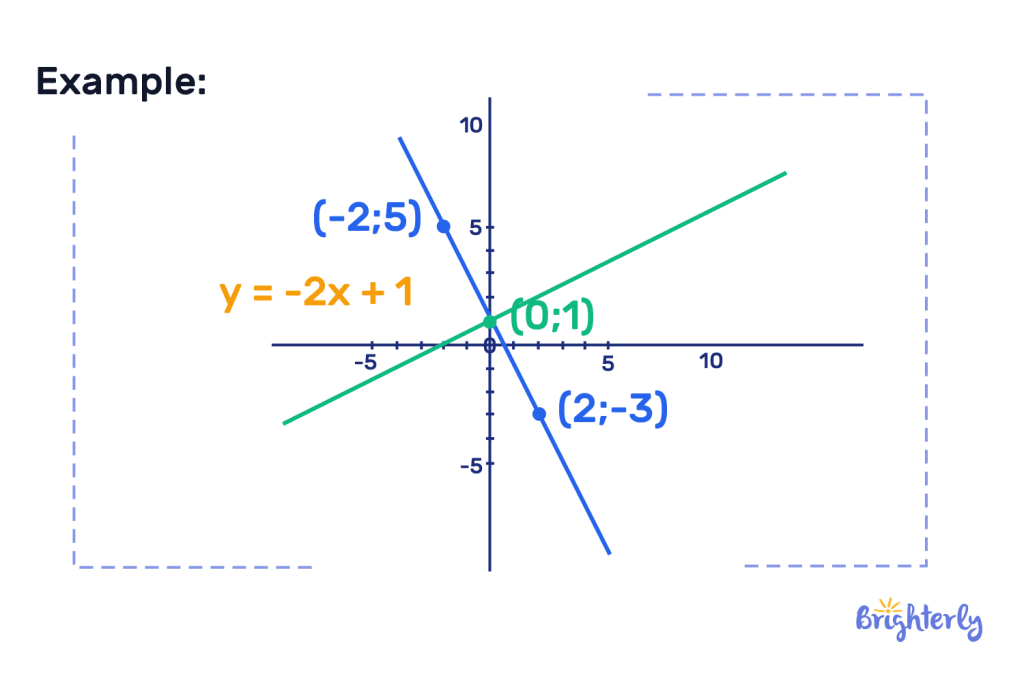
Perpendicular lines and parallel lines: difference
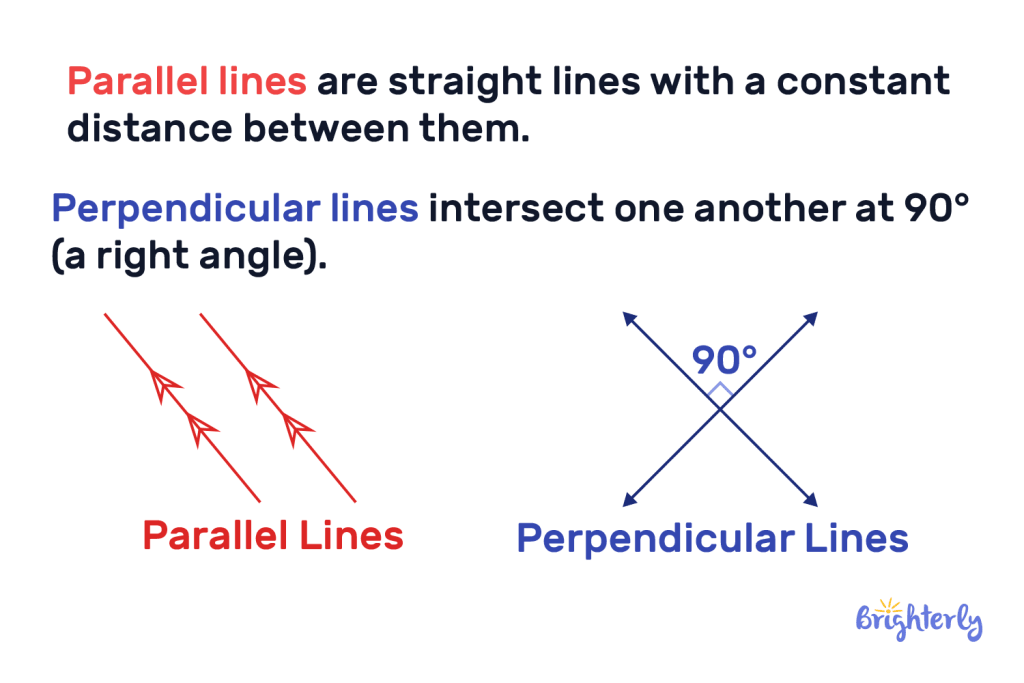
Perpendicular lines and parallel lines are two different concepts in geometry, and they cannot both be true of the same two lines. Perpendicular lines will always intercept, and at that interception, they will always create a right angle, also known as a perpendicular angle. Perpendicular lines do not have equal slopes. They are inverse reciprocals, meaning that eventually, the two lines can and will intersect at 90°.
Parallel lines are equidistant to one another and can never, ever meet – even if they go on infinitely. This is because they are always the same distance apart because they have the same slope, therefore there is never a meeting point between the two. Parallel lines have equal slopes with a constant distance between them.
What are perpendicular sides?
Perpendicular sides are sides in a shape that meet at a right angle (AKA a perpendicular angle). Perpendicular sides are formed of perpendicular lines, but they form a closed shape. Not all perpendicular lines need to form a closed off shape.
There are a number of geometrical shapes that have perpendicular sides, including:
- Squares
- Rectangles
- Right-angled triangles
- Right-angled trapezoids
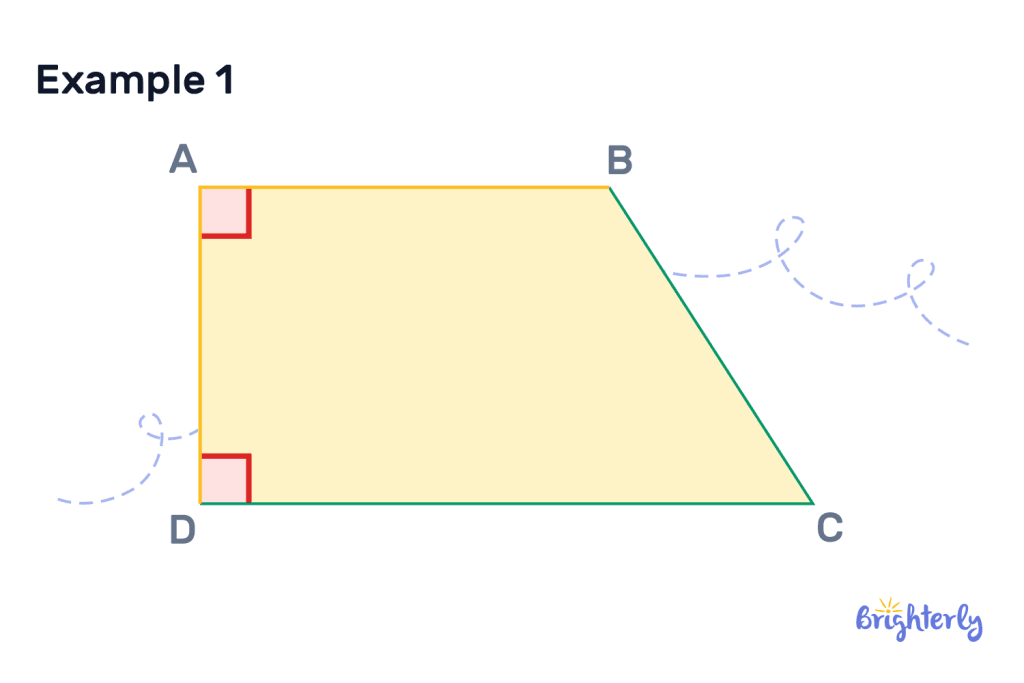
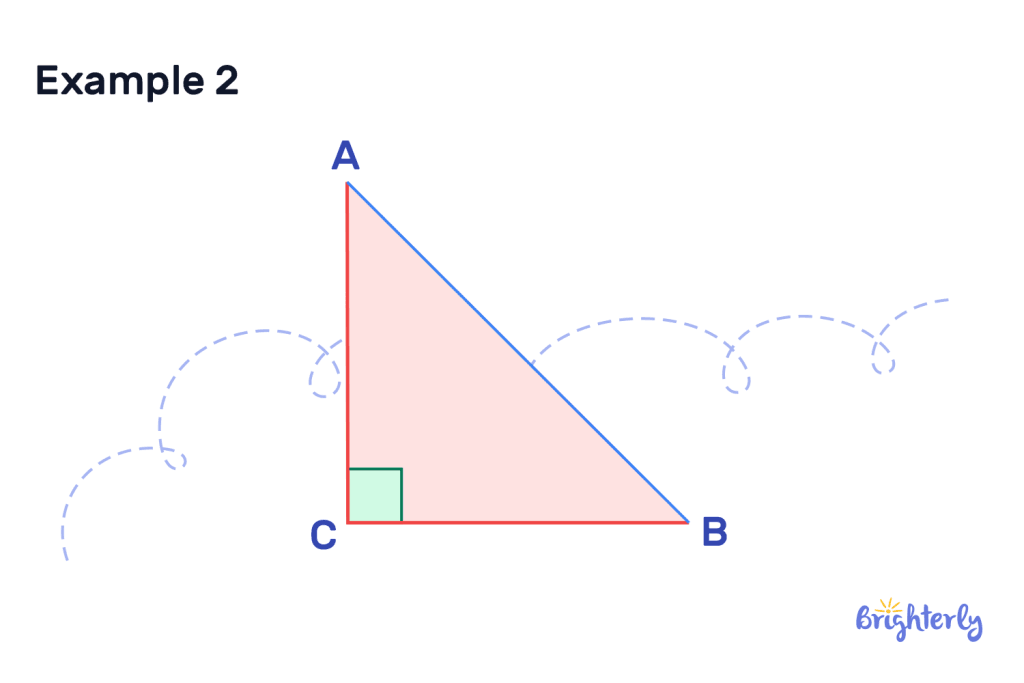
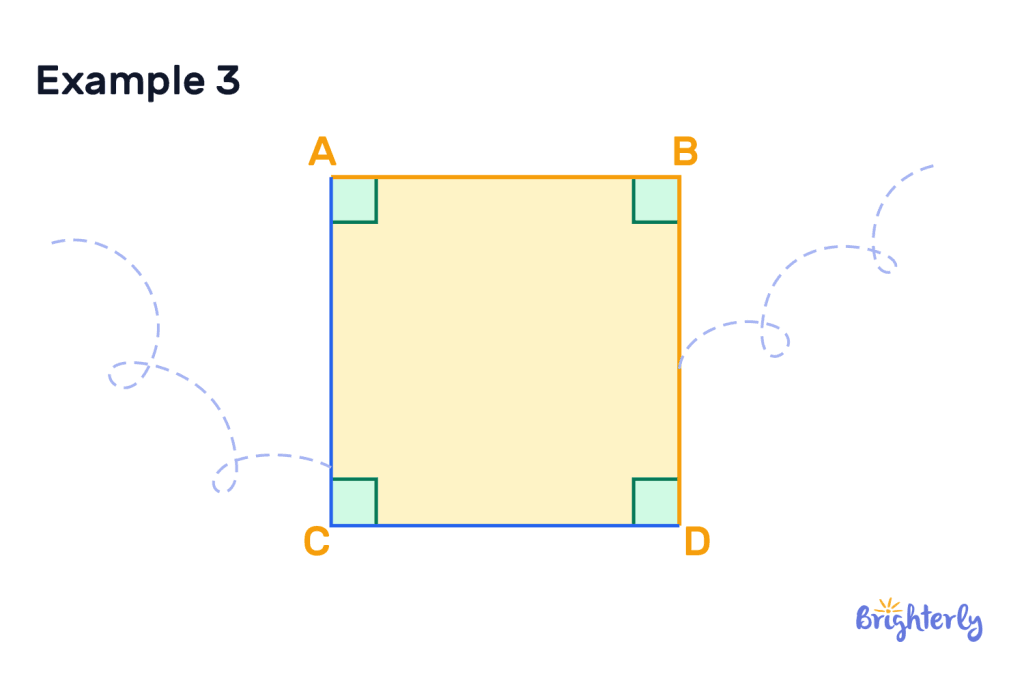
Construction of perpendicular lines
The construction of perpendicular lines is really easy once you know how to do it! We cover two important and easy methods of constructing perpendicular lines here:
- Drawing a perpendicular line using a protractor
- Drawing a perpendicular line at a given point on a line using compass
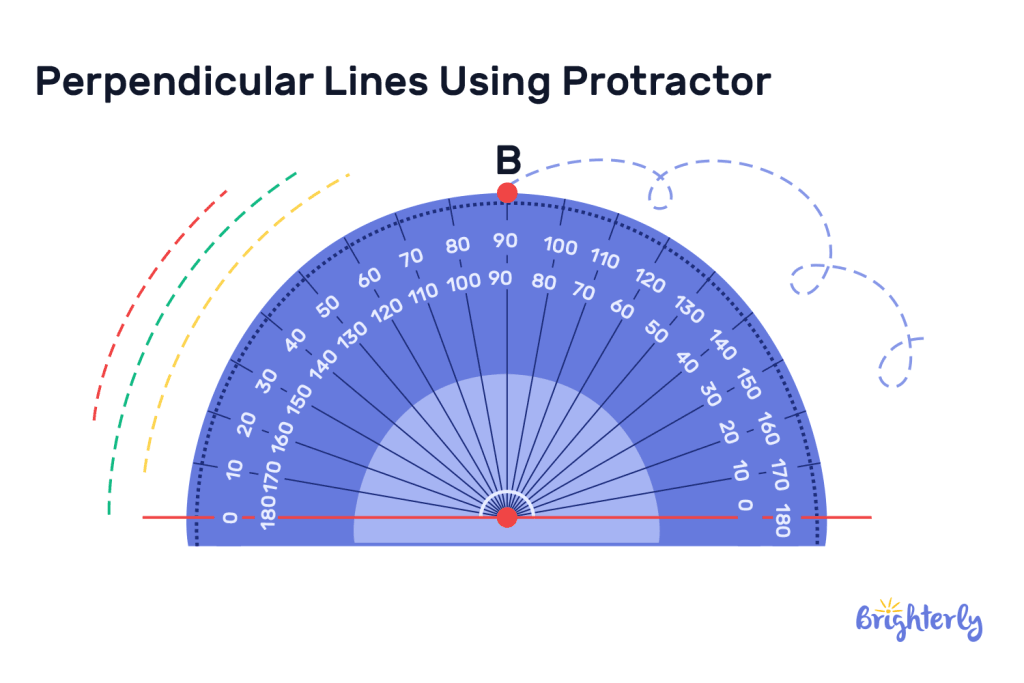
Drawing a perpendicular line using protractor
Drawing a perpendicular line using a protractor is arguably the easiest method of drawing a perpendicular line. Simply follow these quick, straightforward steps:
- Draw a straight line parallel to the top and bottom of your paper – we recommend using a ruler for this to make sure it’s perfectly straight
- Place your protractor onto your paper, setting it on top of your line so the line is parallel to your protractor’s baseline.
- Find the 90° mark on your protractor and draw a little line at this point on the line you’ve drawn
- Move your protector to the end of your newly created line, which adjusts the baseline
- Make another little parallel line at the 90° mark again
- Use a straight line to connect the two small lines that you’ve made, which will run at a 90° angle (or a perpendicular angle) to your original line.
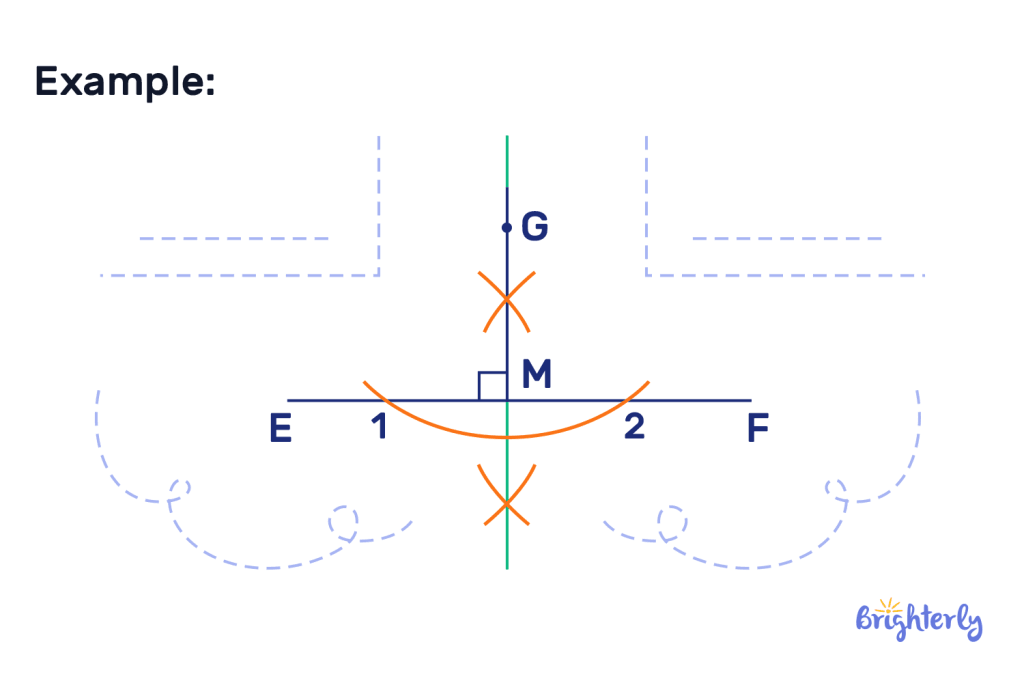
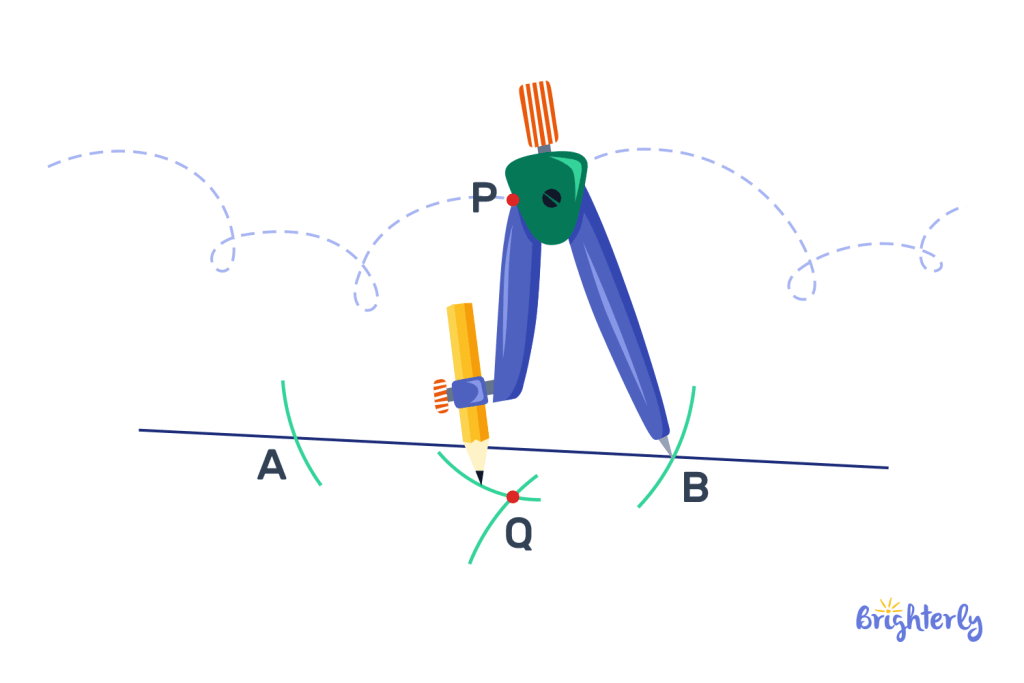
Drawing a perpendicular line at a given point on a line using compass
If you have a line, and a given point on that line through which you need to draw a perpendicular line with no protractor, you can use a compass instead. It might seem daunting, but it’s straightforward if you follow these easy steps:
- Place the point of your compass on your given point, and draw an arc that sections through your line twice
- Label these intersects as point 1 and point 2
- Place the point of your compass on point 2 and adjust the width so that your pen or pencil is more than halfway towards point 1
- Draw two small arcs, one above your line and one below it
- Place the point of your compass on point 1, and carry out the same action, drawing arcs above and below your line that intersect your previous line
- Now, all you need to do is draw a line through the intersecting points in your arcs above and below your line!
Solved math tasks: examples
Now that you know everything there is to know about perpendicular lines, including the perpendicular definition geometry, we have included some solved math tasks and perpendicular examples below so you can practice your new-found knowledge.
Solved math task 1
Does this trapezoid shape below have any perpendicular lines or perpendicular sides? Explain why or why not.
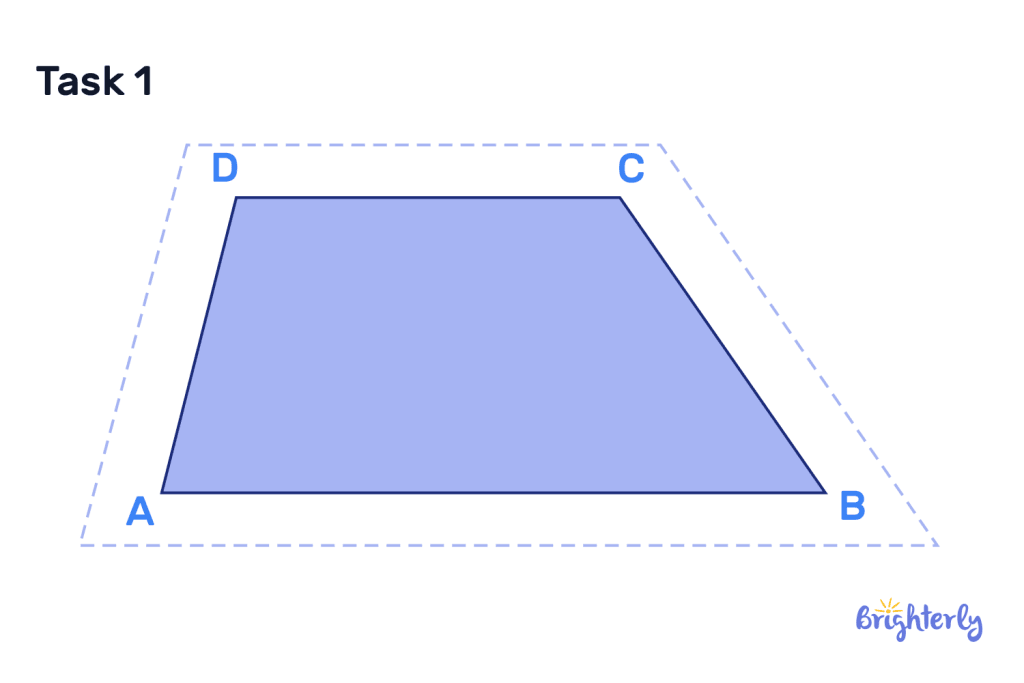
Answer:
| No, the trapezoid does not have any perpendicular lines or perpendicular sides. |
While it has lines and sides that intersect, none of them create a right angle, therefore they are not perpendicular.
Solved math task 2
Using a ruler, draw a straight line on paper that is parallel to the top and bottom of the paper and is 10 cm long. Draw a point above your line that is exactly halfway along the line.
Using that point, draw a perpendicular line through your original line without using a protractor.
Answer:
| Use the method we detailed earlier on using a compass to draw a perpendicular line using a given point. |
Solved math task 3
Take a look at this diagram. Is OA perpendicular to AB? And what shape will this indicate if you connect the two lines?
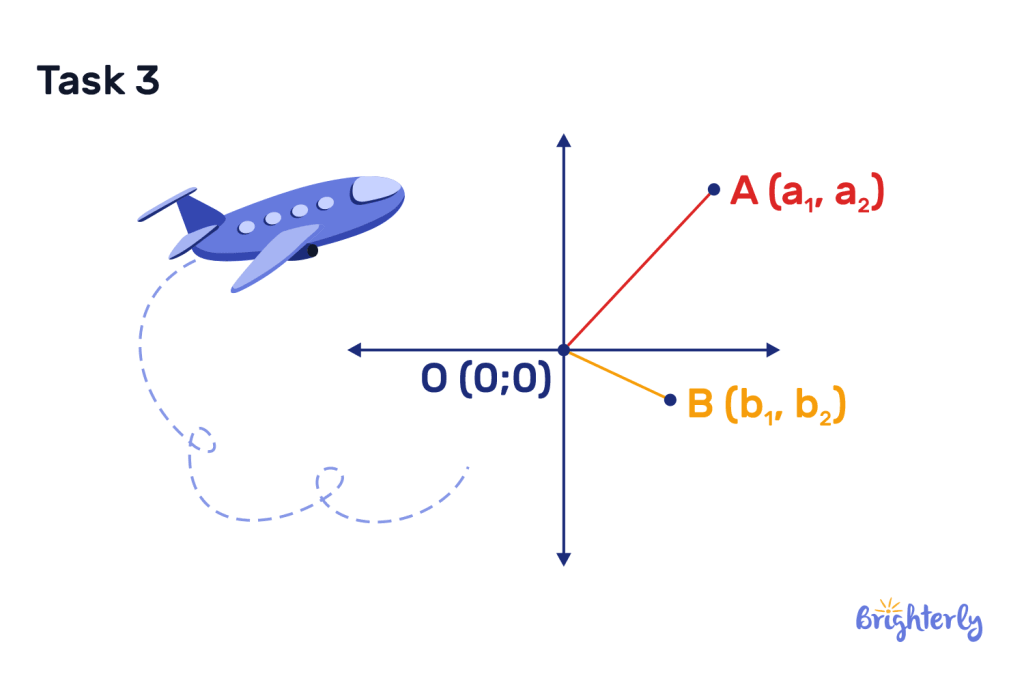
Answer:
| Yes, these lines are perpendicular, because they create a right angle. If we connect both lines, we get a right-angled triangle. |
You can use a protractor to work out the right angle at these perpendicular line intersects, then draw the line from point A to point B to reveal a right-angled triangle.
Perpendicular lines: practice math problems
Perpendicular lines worksheets
Now you have mastered the concept of perpendicular lines, it’s time to put your mathematical wizardry to the test. We’ve created a range of math worksheets featuring perpendicular lines and related math concepts to help you practice and apply your knowledge.