Prime Numbers – Definition with Examples
reviewed by Jo-ann Caballes
Updated on December 19, 2024
Prime numbers are a unique part of mathematics and are crucial for algebra, geometry, computer sciences, and cryptography. This article provides you with a deep delve into this topic, from the prime number definition with examples to how to calculate it and distinguish it from other number types.
What Are Prime Numbers?
Speaking of what prime numbers are, it’s safe to say that it’s a natural number more than 1 that has no divisors other than 1 and itself. In other words, a prime meaning in math is that this number cannot be exactly divided by any whole number except for 1 and itself.
Prime number definition
The definition of a prime number states that it’s a number that can be evenly divided only by 1 and itself.
For instance, you can divide 4 in multiple ways: by 1, by 4, and as the sum of two 2 (since 2 x 2 = 4). It means that 4 can’t be the prime number.
But 5 equally divides only by 1 and by 5. In other cases, we won’t get a whole number. If we try to divide 5 by 2 (5 ÷ 2), we will get a 2.5, which can be counted as a decimal fraction or rational number 5/2. But it’s still not a whole number! So, 5 will count as the prime number as we can divide it by 1 and by itself to get a whole number as the result.
The smallest prime number is 2, as you can divide it only by 1 (as 2 ÷ 1 = 2) or by itself (2 ÷ 2 = 1).
Prime number examples
2, 3, 5, 7, 11,13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97. These are all prime numbers under 100. All other numbers have at least an additional way to divide and get a whole number as a result.
Properties of Prime Numbers
Prime numbers have several recognizable properties. Let’s examine them in detail.
Prime Numbers Chart
A prime numbers chart, or Eratosthenes chart, is a numerical table that records all prime numbers and prime factors.
A chart of prime numbers is one of the quickest ways of identifying those numbers. It comes with prime numbers already determined and arranged in rows and columns with the prime numbers highlighted.
The prime numbers chart gives you a quick reference for identifying specific numbers. It can also teach concepts related to prime numbers, such as factorization and divisibility. It even helps with pattern recognition, as when students define a prime number, they can visualize patterns and sequences, leading to further exploration and discovery.
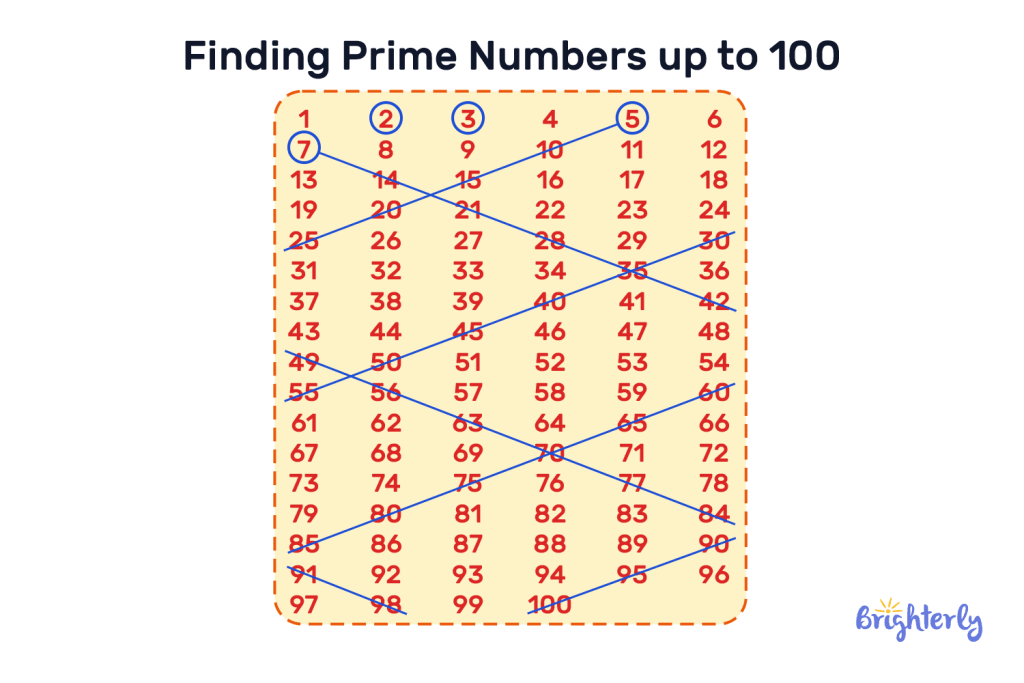
Easy Ways to Find Prime Numbers
There are many ways to find prime numbers, but most of them are complicated. The easiest way is called the Sieve of Eratosthenes. Here we showcase you how to easily find prime numbers 1 to 100, but you can use it even with larger numbers:
- Create a list of consecutive integers from 2 to the given limit.
- Mark the first number (2) as prime.
- Cross out all multiples of 2 (starting from 4, every second number).
- Find the next unmarked number (3), and mark it as prime.
- Cross out all multiples of 3 (starting from 6, every third number).
- Repeat steps 4 and 5 for the next unmarked number (5, 7, etc.) until the square root of the limit is reached.
- The remaining unmarked numbers are prime.
This scheme perfectly works with prime numbers 1-100. After that, it becomes more complicated, but still works well.
Prime Factorization
Another relatively easy way to determine numbers that are prime is to use the prime factorization method. The operating principle is similar to Eratosthenes’ Sieve, but with minor changes:
- Divide the number into factors.
- Check how many factors that number has. If the number of factors is more than 2, then it is composite. For instance, 8 has four factors: 1,2,4 and 8. So we can state that it’s not a prime.
- All prime numbers greater than 3 can be represented by the formula 6n+1 and \(6n -1) for n greater than equal to 1. Exception if the number ends with 5 or higher multiples of 7, such as 49, 77, 91. For instance, 5=6×1−1, 7=6×1+1, 11=6×2−1, 13=6×2+1.
In this case, a chart of prime numbers 1-100 will look like the next illustration.
Prime Formulas
While there isn’t a simple, direct prime formula, there are some interesting patterns and formulas that can help identify potential numbers relatively fast:
- 6n ± 1: Most numbers are prime numbers (except 2 and 3) and can be expressed in the form 6n ± 1, where n is a natural number. However, there are still a lot of exceptions, so you need to double-check.
- Wilson’s Theorem: A natural number p > 1 is a prime number if only: (p-1)! ≡ -1 (mod p). While this is a great way to define prime numbers, it’s not practical due to the complex factorial calculation.
You can’t randomly share the example of prime numbers, as no formula perfectly works with all numbers without exceptions. The search for a simple formula is still an open problem.
List of Prime Numbers
While there is no complete list of all prime numbers, as there is an endless amount of options, we can help you with the most common variants.
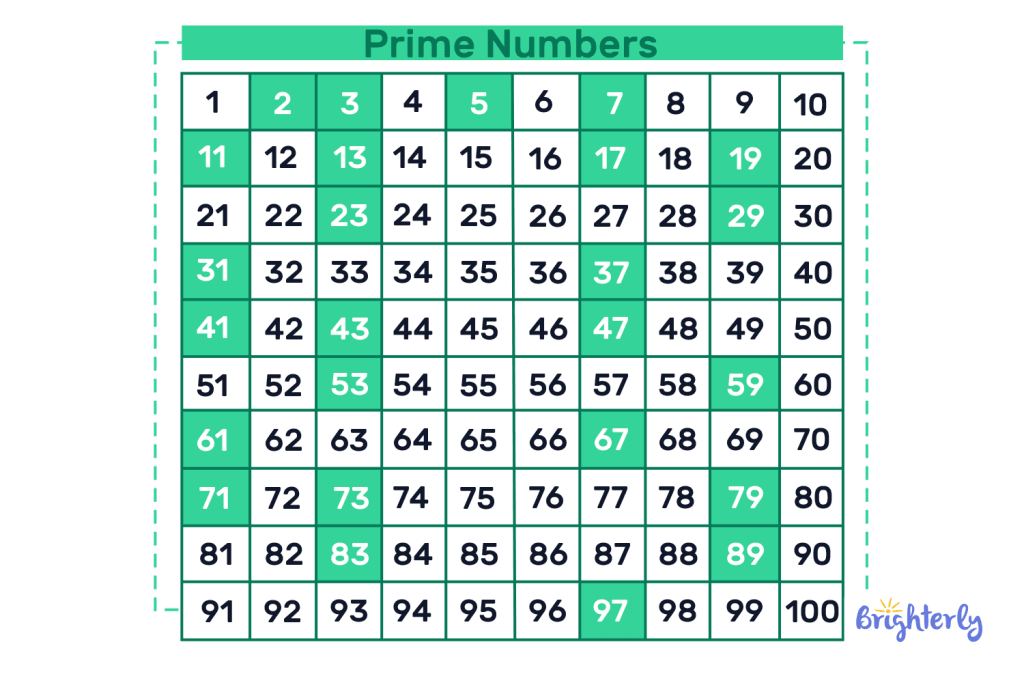
List of Prime Numbers between 1 and 100
Speaking of how many prime numbers are between 1 and 100, there are only 25 numbers on this list. You can see them in the picture below.
The lowest prime number is 2.
List of Prime Numbers between 1 and 200
Between 1 and 200, there are 46 prime numbers in the list. You can see them in the picture below.
Prime Numbers between 1 and 1000
If you are interested in the prime numbers between 1 and 1000, there are 168 numbers on the list. You can see them in the picture below.
Prime Numbers and Composite Numbers
Many features differentiate a prime number from a composite number. A prime number definition states it is a natural number greater than 1 with just two factors. Meanwhile, composite numbers are greater than 1 with more than two factors. So, they can be easily divisible by more than two factors.
Speaking of prime numbers 1-6, number 1 is neither; 2 is the only even prime number. 3 and 5 are prime. Meanwhile, 4 and 6 are composite since they can be divided in more than two ways.
Prime Numbers and Co-Prime Numbers
While prime numbers are considered singularly, co-prime numbers are examined in pairs. A pair of numbers with no common factor except for 1 are considered co-prime numbers.
Co-prime numbers can either be prime or composite since the greatest common factor (GCF) of the numbers is 1.
For instance, 5 and 9 are co-prime because they have no common factors other than 1. The factors of 5 are 1 and 5. The factors of 9 are 1, 3, and 9. And while 5 is one of the prime numbers between 1 and 10, and 9 is the composite, they act as co-prime to each other.
Prime number chart
A prime number chart to 100 is relatively easy since it works with the Sieve of Eratosthenes and prime numbers.
Solved Examples of Prime Numbers
To solidify your knowledge, we want to practice some solved examples of prime numbers with you.
Solved math example 1
We have numbers from 1 to 25. Which of these numbers is prime? Why?
Answer
The prime numbers from 1 to 25 are 2, 3, 5, 7, 11, 13, 17, 19 and 23.
| A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. |
Solved math example 2
Imagine that you see a line of numbers from 130 to 175. Which of the following numbers are prime? How do you determine prime numbers if they are larger than 100?
Answer
| The prime numbers between 130 and 175 are 131, 137, 139, 149, 151, 157, 163 and 167. |
Use the Sieve of Eratosthenes and prime numbers to define a prime number. They still work even with numbers larger than 100.
Prime Numbers: Practice Math Problems
Prime Numbers: Worksheets
A prime number meaning is simple and simultaneously so complex, even for adults. That’s why we created free math worksheets that can help you to boost your knowledge skills:
- Prime and Composite Numbers Worksheets
- Dividing Whole Numbers Worksheets
- Number Sequence Worksheets
- Ratios And Rates Worksheets
- Ordering Numbers Worksheets
- Order of Operations with Exponents Worksheets
Frequently Asked Questions
Is 1 a prime number?
No, 1 is not a prime number. A definition of a prime number states that it must have exactly two distinct positive divisors: 1 and itself. Since 1 only has one divisor, it doesn’t fit the definition of a prime number.
Can a prime number be negative?
No, a prime number cannot be negative. A prime number meaning explains that it’s a natural number greater than 1 with exactly two distinct positive divisors: 1 and itself. Negative numbers don’t fit this criteria.
What is the difference between a prime number and a co-prime number?
The main difference between a prime number and a co-prime number is that all prime numbers are co-prime to each other; co-prime numbers don’t have to be prime themselves.
What is the smallest prime number?
2 is the smallest prime number, as it has only itself and 1 as the divisors.
What is the largest known prime number?
As of 2025, the largest known prime number is a Mersenne prime, discovered in 2018. It’s a massive number with over 24 million digits. The Great Internet Mersenne Prime Search (GIMPS) project is actively searching for larger prime numbers.
Which numbers are not prime numbers?
Any natural number greater than 1 that can be divided by 1, itself, and any other number is not a prime number. For instance, 4 can be divided by 1,2 and 4. So, we can’t count 4 as a prime number.
Need help with Numbers?
- Is your child having trouble understanding numbers concepts?
- An online tutor could provide the necessary help.
Choose kid's grade
Does your child need extra support with grasping the basics of numbers? Start lessons with an online tutor.
