Pythagorean Triples
reviewed by Jo-ann Caballes
Updated on October 1, 2024
Here at Brighterly, we make math concepts fun and easy to understand. Middle-school geometry concepts like Pythagorean triples may appear daunting. But with a little practice and some engaging activities, your kid can become a master of this concept – and enjoy the beauty in their underlying patterns.
Here, we’ll cover the Pythagorean triples definition and calculations and share practice worksheets and Pythagorean triples tests.
What are Pythagorean triples?
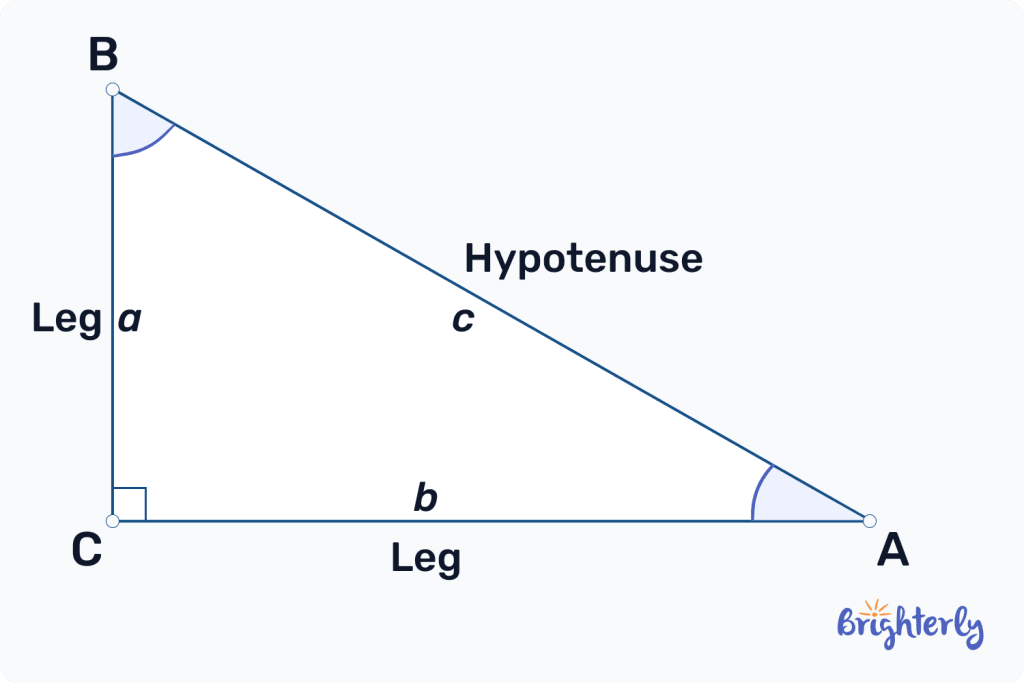
Pythagorean triples are an intriguing math concept that describes the relationship between the lengths of each side of a right-angled triangle.
These lengths, formed of three positive integers (a, b, c), create a pattern that relates to the Pythagorean theorem. The Pythagorean theorem dictates the relationship between the lengths of each side of a right-angled triangle.
According to the Pythagorean theorem, the square of the length of the hypotenuse (the longest of the three sides and the one facing the right angle) is the sum of the other two sides squared: a² + b² = c².
Pythagorean triples: definition
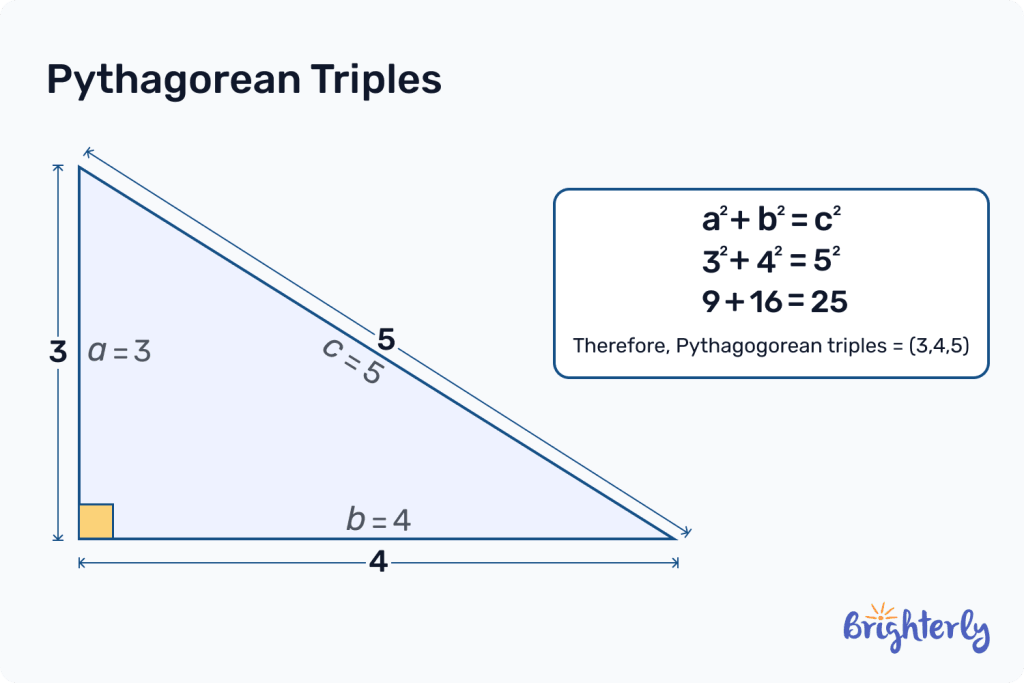
The Pythagorean triples definition is three whole numbers (positive integers) that fit into the sum dictated by the Pythagorean theorem: a² + b² = c². In a Pythagorean triple, the numbers will always be listed from smallest to largest – for example, the smallest Pythagorean triple of (3, 4, 5).
What Are Pythagorean triples in geometry?
Pythagorean triples in geometry dictate the lengths of each side of a right-angled triangle. If you’re able to find three whole numbers, also known as positive integers, that fit into the equation of a² + b² = c², then you can create a right-angled triangle.
Pythagorean triples also relate to other aspects of geometry and can fit into other shapes, including rectangles, triangles and some variations of polygons. If you can draw a right-angled triangle within these shapes, you can use the Pythagorean triples concept to work out the hypotenuse length.
What are primitive Pythagorean triples?
Primitive Pythagorean triples are the smallest common denominators in a Pythagorean theorem equation. This means all the numbers cannot be divided by any number except 1.
The smallest known primitive Pythagorean triple is 3, 4, 5. All non-primitive Pythagorean triples can be reduced to their primitive Pythagorean triple by dividing all numbers by their largest common divisor.
Pythagorean triples: examples
Here are some Pythagorean triples examples using the smallest primitive triple (3, 4, 5):
Pythagorean triples list
Here’s a list of all 16 primitive Pythagorean triples utilizing numbers up to 100:
| (3, 4, 5) | (5, 12, 13) | (7, 24, 25) | (8, 15, 17) |
| (9, 40, 41) | (11, 60, 61) | (12, 35, 37) | (13, 84, 85) |
| (16, 63, 65) | (20, 21, 29) | (28, 45, 53) | (33, 56, 65) |
| (36, 77, 85) | (39, 80, 89) | (48, 55, 73) | (65, 72, 97) |
There’s no limit to the number of Pythagorean triples, so it would be impossible to list all Pythagorean triangles.
Common Pythagorean triples
The most common Pythagorean triples you might have come across before will likely be small primitive Pythagorean triples. You may have come across these triples in math-based puzzles or school classes:
- (3, 4, 5)
- (5, 12, 13)
- (7, 24, 25)
- (8, 15, 17)
- (9, 40, 41)
Pythagoras triples formula
The Pythagoras theorem mathematical formula helps you to generate your Pythagorean triples.
The basic formula is as follows: a² + b² = c²
A and b represent the two sides of your right-angled triangle that form the right angle. C represents the hypotenuse, the final side opposite the right angle.
How to form Pythagorean triples
To form a Pythagorean triple, you can also use this method that takes you through extra steps.
First, you’ll need to pick two whole numbers, which will be your m and n. Your m number must be larger than your n number.
- a = m² – n²
- b = 2mn
- c = m² + n²
In order for this formula to work, m and n must be positive integers (whole numbers). Both your m and n should also be coprime (where they both aren’t divisible by a number bigger than 1).
Once you’ve mastered this formula, you can create a limitless number of Pythagorean triples, each with its own individual lengths for the three sides of your right-angled triangle.
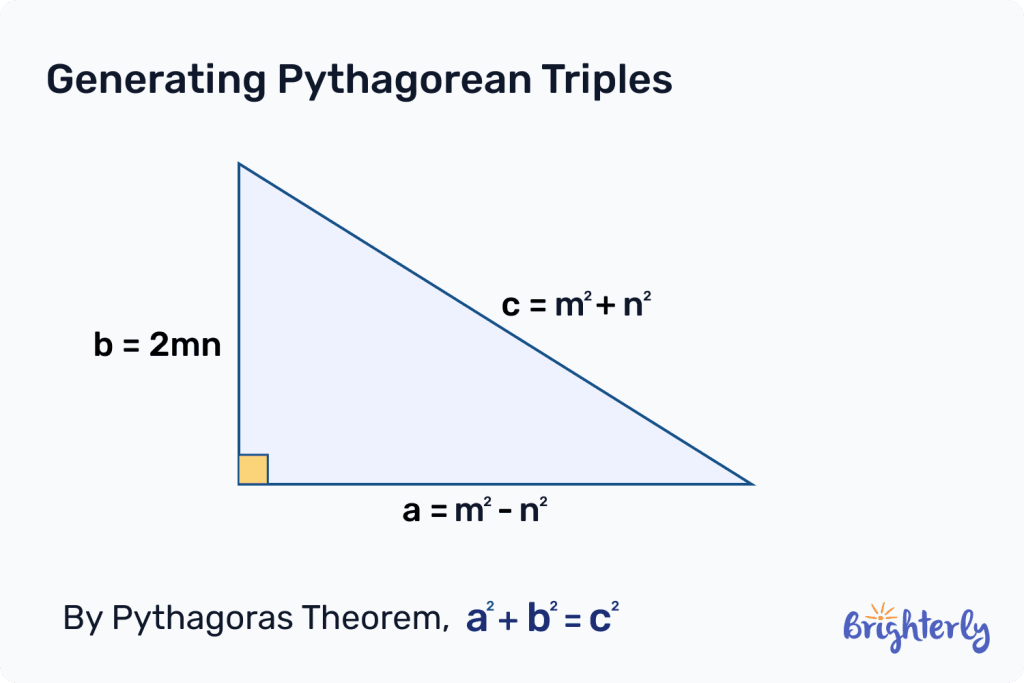
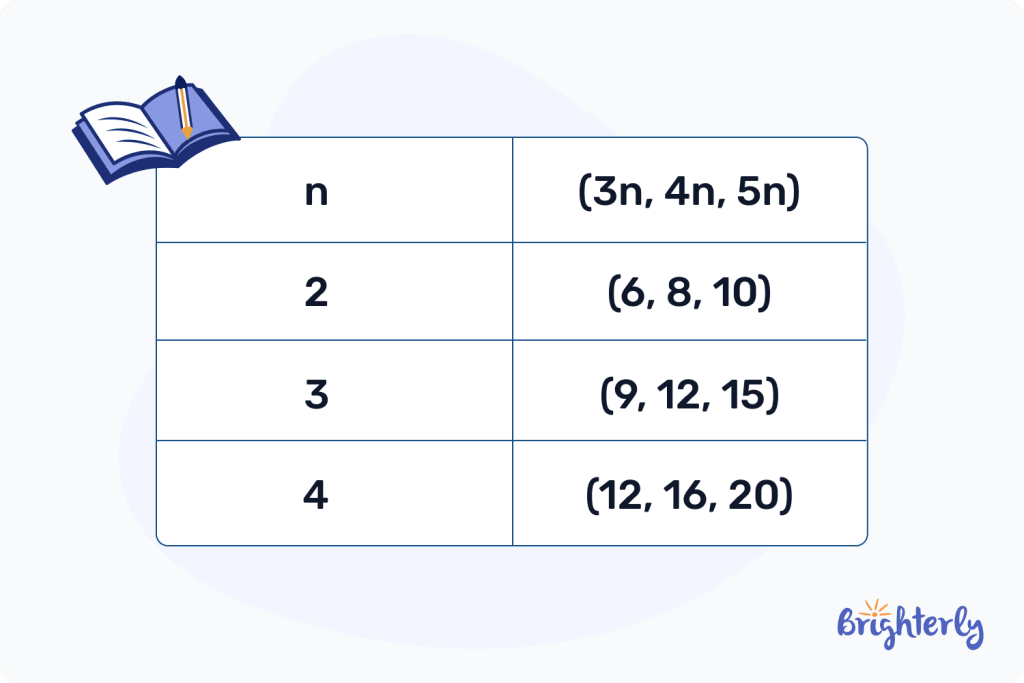
Generation of Pythagorean triples
To generate Pythagorean triples, we recommend using the formulas detailed above. We’ve also included a helpful graphic below on the generation of Pythagorean triples so you can see how this works in relation to your right-angled triangle.
How can I find Pythagorean triples?
There are a few different ways of finding Pythagorean theorem triples that we have outlined above. The basic formula will always work, providing your numbers fit into it. If you want to work out your numbers from scratch, you can use the longer method where you generate an m and n number first.
Pythagorean triples formula: proof
The proof for the Pythagorean triples formula can be discovered if we delve deeper into how the Pythagorean theorem equation works.
If we take our earlier example of choosing numbers of m and n, where m is larger, we can break this down by substituting the formula’s expressions for a, b and c.
- Swap out the expressions for a, b and c: (m² – n²)² + (2mn)² = (m² + n²)²
- Expand the squares of the numbers: m⁴ – 2m²n² + n⁴ + 4m²n² = m⁴ + 2m²n² + n⁴
- Simplify the equation: m⁴ – 2m²n² + n⁴ + 4m²n² = m⁴ + 2m²n² + n⁴
- You’ll see that the formula is valid because the equation is true.
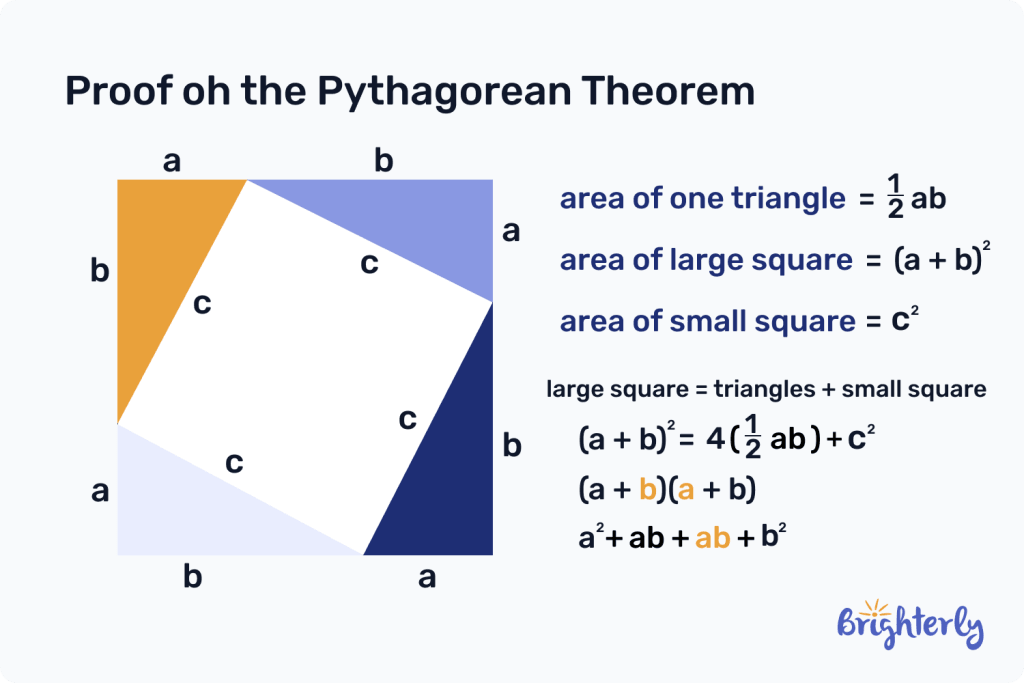
You can also prove the Pythagorean theorem and Pythagorean triples theorem by creating a square. You then create another square, placed at a different angle, within your original square to create four right-angled triangles. Then, you can use the following equations to understand the relationships between the shapes and prove Pythagorean theorem triples.
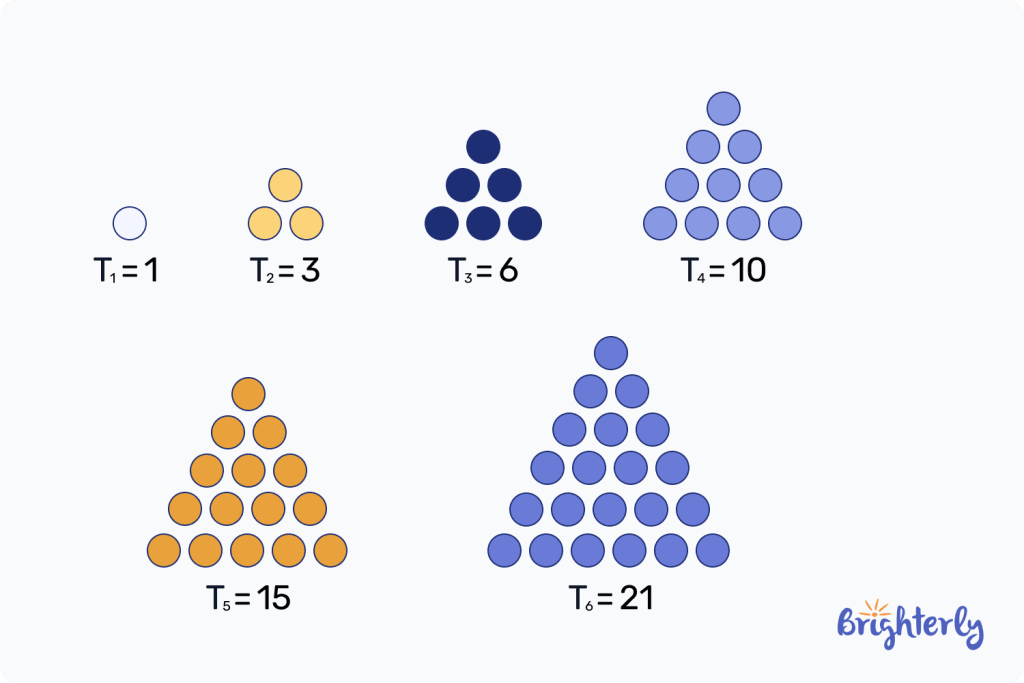
What are triangular numbers?
Triangular numbers are a sequence of numbers that represent shapes that can form an equilateral triangle. So for example, 1 on its own can fit inside an equilateral triangle. 3 is the next number if two of the shapes are on the bottom and one is on the top.
6 comes next, with 3 shapes on the bottom, two in the middle and one on the top. For each additional triangular number, you would simply add an extra row at the bottom with one more shape in it than the previous row.
Solved math tasks: examples
We have included some solved Pythagorean theorem triples tasks below to help you practice Pythagorean triples.
Is (5, 12, 13) a Pythagorean triple?
Solution:
- Put the numbers into the Pythagorean theorem equation – 5² + 12² = 13²
- Work out your sum: 5² (25) + 12² (144) = 12² (169)
- If your sum is correct, the sequence is a Pythagorean triple!
Answer:
| Yes, the sum is a Pythagorean triple |
If we have the sequence (a, 15, 17), what number is a?
Solution:
- Work out what your two known numbers will be: a² + 15² = 17² becomes a² + 225 = 289.
- Take your second number away from your third: 289 – 225 = 64.
- Work out the square root of that number: 64 ÷ 8 = 8.
Answer:
| A is 8 |
Revising and understanding these questions will help you to pass Pythagorean triples tests.
Pythagorean triples: practice math problems
Pythagorean triples worksheets
Here, we have listed some Brighterly math worksheets that can help your kid understand the concept of Pythagorean triples: