Acute Scalene Triangles – Definition With Examples
Updated on December 19, 2024
There are a lot of different types of triangles. The acute scalene triangle is one of them.
Here, we discuss the acute scalene triangle definition, the acute scalene triangle examples, and practice problems to help you understand this shape.
What Are Acute Scalene Triangles?
Acute scalene triangles are a mixture of a scalene and an acute triangle.
Basic Definition and Characteristics
The acute scalene triangle may be defined as a type of triangle with the traits of the acute and scalene triangles. This is because this type of triangle has three different angles on each side, like the scalene triangle, and each angle is less than 90 degrees, like the acute angle.
What does an acute triangle look like?
The acute triangle has three interior angles, each less than 90 degrees but cumulatively adding up to 180 degrees. Acute triangle examples include diagonally cut sandwiches or steep roof trusses.
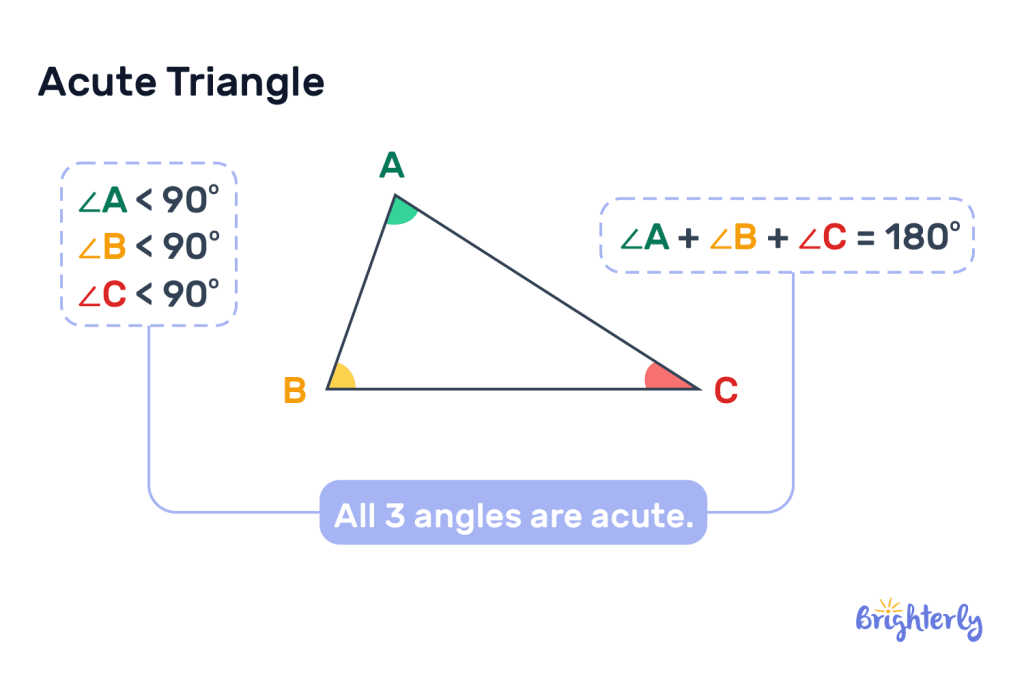
Definition of Acute Angles
An acute angle is an angle less than 90 degrees. A triangle that is made up of only acute angles in all three interior angles is acute.
Definition of Scalene Triangles
The definition of a scalene triangle is a type of triangle with unequal lengths and different interior angles.
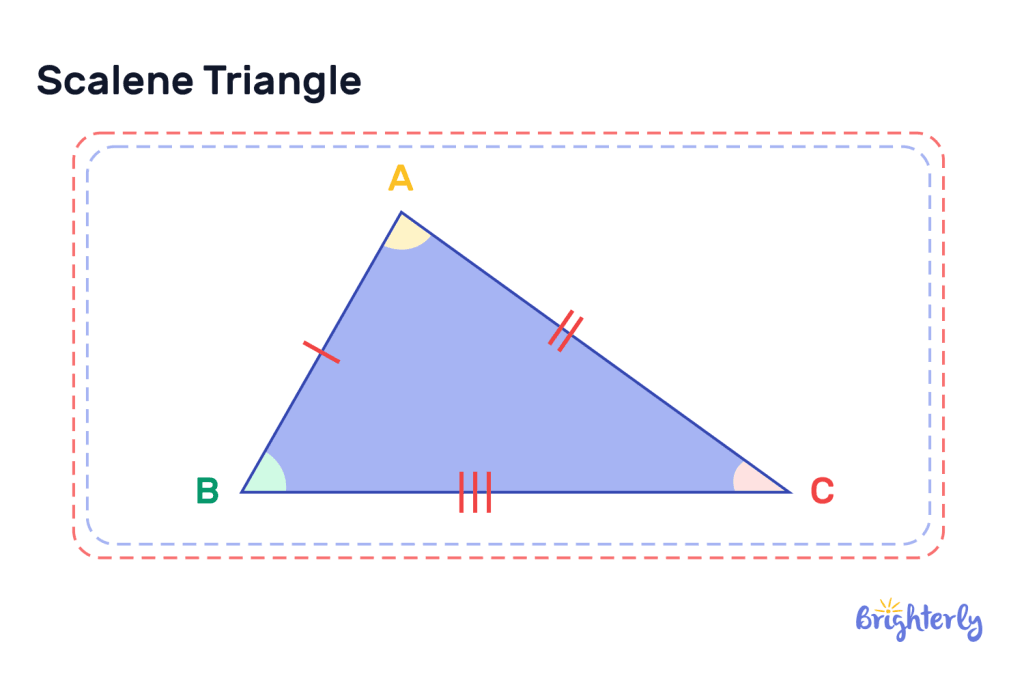
Example of scalene triangle
There are different scalene triangle examples depending on the scalene triangle angles. It can be exactly 90 degrees (right scalene triangle), above 900(obtuse scalene triangle), or less than 90 degrees (this is the acute scalene triangle).
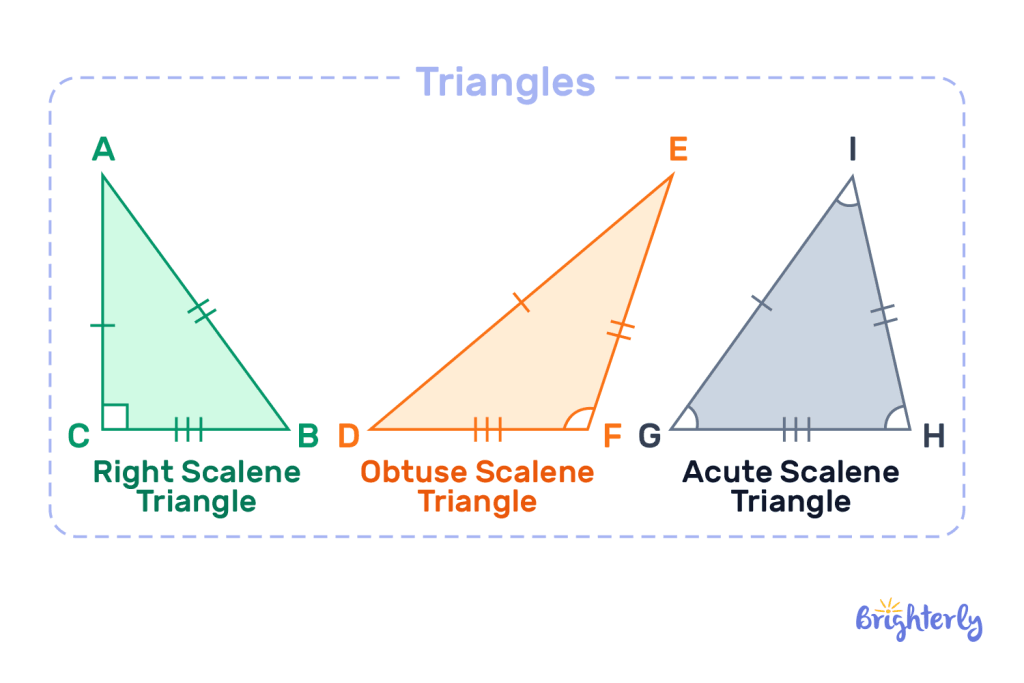
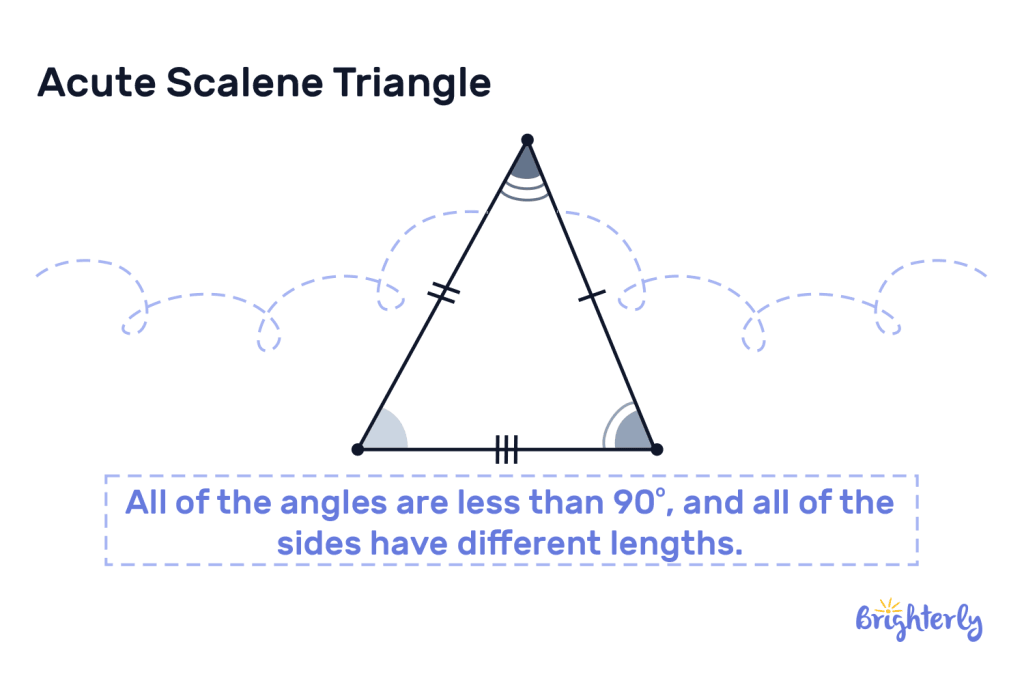
Properties of Acute Scalene Triangles
Here are some distinct properties unique to the scalene acute triangle:
- Each and all of the angles are less than 90 degrees
- The interior angles have different degrees
- The triangle has unequal sides
- The interior angles measure 180 degrees when added.
Properties of Acute Angles
To easily identify the acute triangle, here are some properties it possesses:
- The angles are always less than 90 degrees
- The sum of the angles is 180 degrees
- The acute triangle can be of different types: isosceles, equilateral, and scalene triangles.
Properties of Scalene Triangles
The scalene triangle also has its own set of properties:
- The angles are different from each other
- The sides are unequal
- The sum of the interior angles is 180 degrees
- It has different types too: obtuse, right-angled, and acute.
Difference Between Acute Scalene Triangles and Other Triangle Types
As mentioned above, the acute scalene triangle is a type of triangle, which means there are other types with unique characteristics and features. Let’s go over some of them and see the differences between them and the acute scalene triangle.
Acute Scalene vs. Obtuse Triangles:
| Acute Scalene triangle | Obtuse triangle |
| An acute scalene triangle has all three interior angles below 90 degrees | The obtuse triangle has one angle above 90 degrees and two angles below 90 degrees |
| All the sides and angles are different | All the sides and angles may be different or two of the sides may be the same |
| The acute scalene triangle has the properties of an acute and scalene triangle | The obtuse triangle can be an obtuse scalene triangle or an obtuse isosceles triangle |
Acute Scalene vs. Equilateral Triangles:
| Acute Scalene triangle | Equilateral triangle |
| All the sides are unequal in length and the angles are less than 90 degrees | All the sides are equal in length and the angles as well (60 degrees each) |
| It is asymmetrical because of its uneven sides and angles | It is symmetrical because all the sides and angles are equal |
Acute Scalene vs. Isosceles Triangles:
| Acute Scalene triangle | Isosceles triangle |
| It has three sides of unequal length | It has two sides of equal length |
| All the angles are unequal | Two out of the three angles are equal |
| The angles are less than 90 degrees | It can have acute angles, one right angle (90 degrees), or one obtuse angle |
Brighterly recommends these worksheets for kids to help you better understand the topic of Acute Scalene Triangles.
Geometry of Acute Scalene Triangles
The geometry of the acute scalene triangle includes the properties we examined earlier and the formulas for finding its area and perimeter.
Area of Acute Scalene Triangle
We find the area of the acute scalene triangle by multiplying ½ by the base and by the height of the triangle which is expressed as:
Area = ½ × base × height square units.
When the sides of the acute scalene triangle are known, we can find the area by using a formula known as Heron’s formula. Here it is:
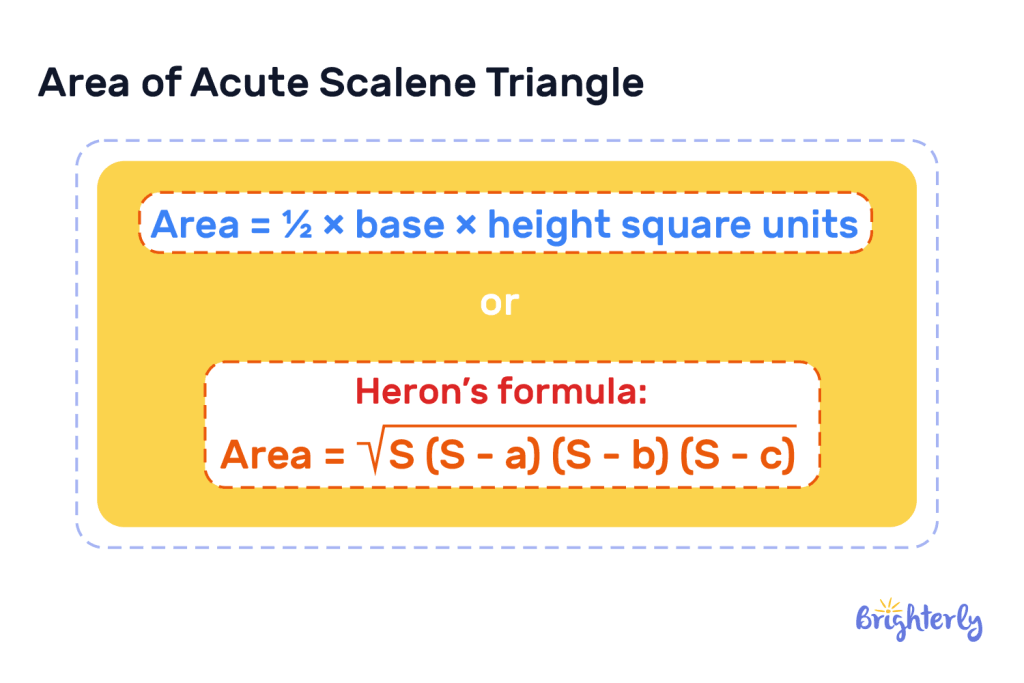
For this formula, S refers to a semi-perimeter and we can find it by adding all the sides of the triangle, then dividing by 2.
Note that in area, your answer must be in square units.
Perimeter of Acute Scalene Triangle
We find the perimeter of the acute scalene triangle by summing all three sides. So, if the sides are a, b, and c, then the formula will be:
Perimeter = (a + b + c)
Constructing Acute Scalene Triangles
Here’s how to construct an acute scalene triangle with a compass and ruler:
- Step 1: We draw a line for the base. This can be any length
- Step 2: With the compass, we draw arcs on each endpoint of the line
- Step 3: We make a point as the vertex or tip of the triangle. The arcs must intersect at this point.
- Step 4: We join the vertex to the endpoints of the triangle’s baseline.
Solving Problems Involving Acute Scalene Triangles
We can solve problems with the acute scalene triangle if the problems include finding a missing angle or an unknown side.
Solved Math Problem 1
An acute scalene triangle has three angles, two of the three are 45 and 75 degrees respectively, what is the third angle?
Answer
Remember that the sum of all the angles is always 180 degrees.
Therefore,
180° — (45° +75°) = 60°
| The missing angle is 60 degrees. |
Practical Applications and Problem-Solving
Acute Scalene triangles exist in practical real-world scenarios in industries such as engineering and architecture. The acute scalene triangle example can be found in roof designs, uniquely shaped buildings, truss structures, and so on.
Practice Problems on Acute Scalene Triangles
Frequently Asked Questions on Acute Scalene Triangles
What defines an acute scalene triangle?
The acute scalene triangle is defined by its angles which are less than 90 degrees (acute) and its unequal sides (scalene)
How is an acute scalene triangle different from isosceles or equilateral triangles?
The equilateral triangle has three equal sides, the isosceles triangle has two equal sides, and the acute scalene triangle has no equal sides.
Can an acute scalene triangle have a right angle?
No. A right angle is 90 degrees but an acute scalene triangle only has angles that are less than 90°.
What type of triangle has three acute angles?
An acute triangle. It can be any of the three types: acute isosceles triangle, acute equilateral triangle, and acute scalene triangle.
Online Winter Math Camp for Grades 1-8
Join us to help your kid achieve their full math potential.
Choose kid's grade
Online Winter Math Camp for Grades 1-8
Join our Math Winter Camp and boost your child's math skills with our best tutors.
