• Math tutors
• /
• Knowledge Base
• /
• Acute Triangle – Definition with Examples

Acute Triangle – Definition with Examples

Camille Ira B. Mendoza

reviewed by Jo-ann Caballes

Updated on October 8, 2024

At Brighterly, we make learning math exciting and engaging for all kids.

Today, as part of our series on shapes, we’re looking at acute triangles.

In this article, we’ll cover the acute triangle definition, the different types of acute triangles and their properties, and share examples of acute triangles and practice math problems.

What is an acute triangle?

An acute triangle is a special type of triangle defined by the size of its internal angles. See the full definition of acute triangles below.

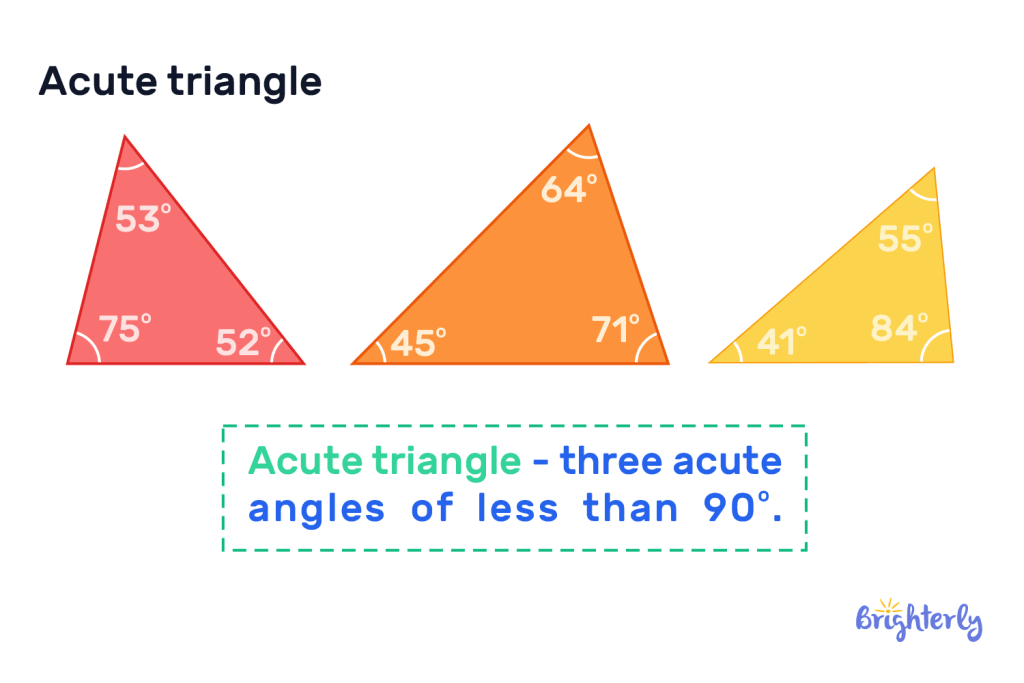
Acute triangle: definition

The acute triangle definition geometry is a triangle with 3 acute angles (less than 90°), which is where the acute triangle name comes from. You’ll see acute triangles of all different shapes in sizes, but they all have angles of under 90°.

Acute triangles: types

There are different types of acute triangles categorized based on the length of their sides. There are three main types of acute triangles:

• Equilateral acute triangles
• Isosceles acute triangles
• Acute scalene triangles

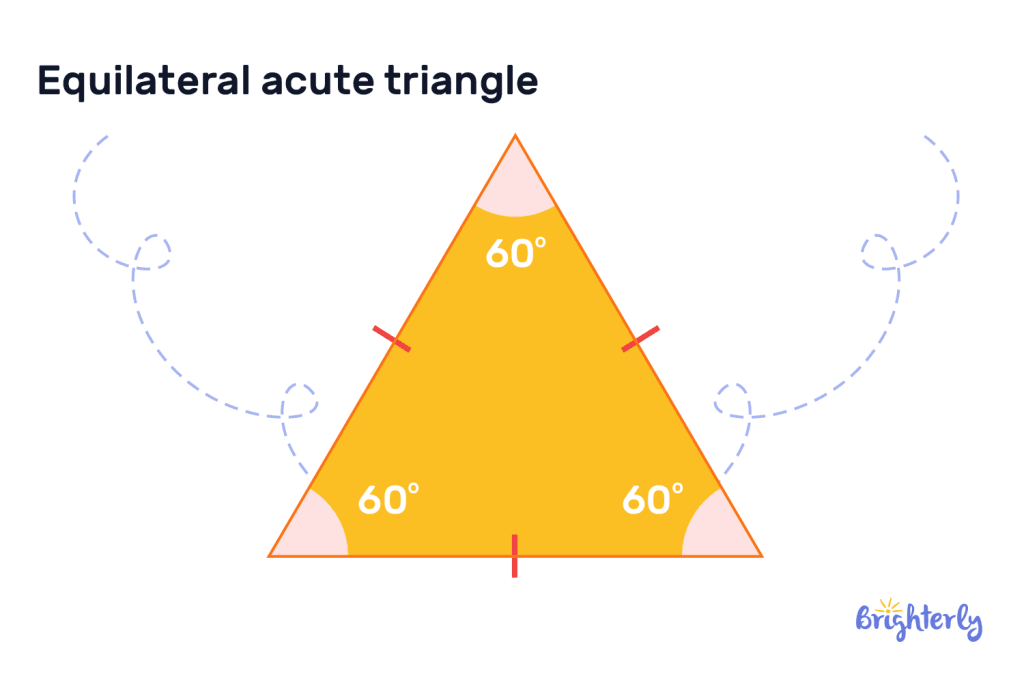
Equilateral acute triangle

An equilateral acute triangle has three sides equal in length, and three angles that are all the same size. Each angle will always measure 60°.

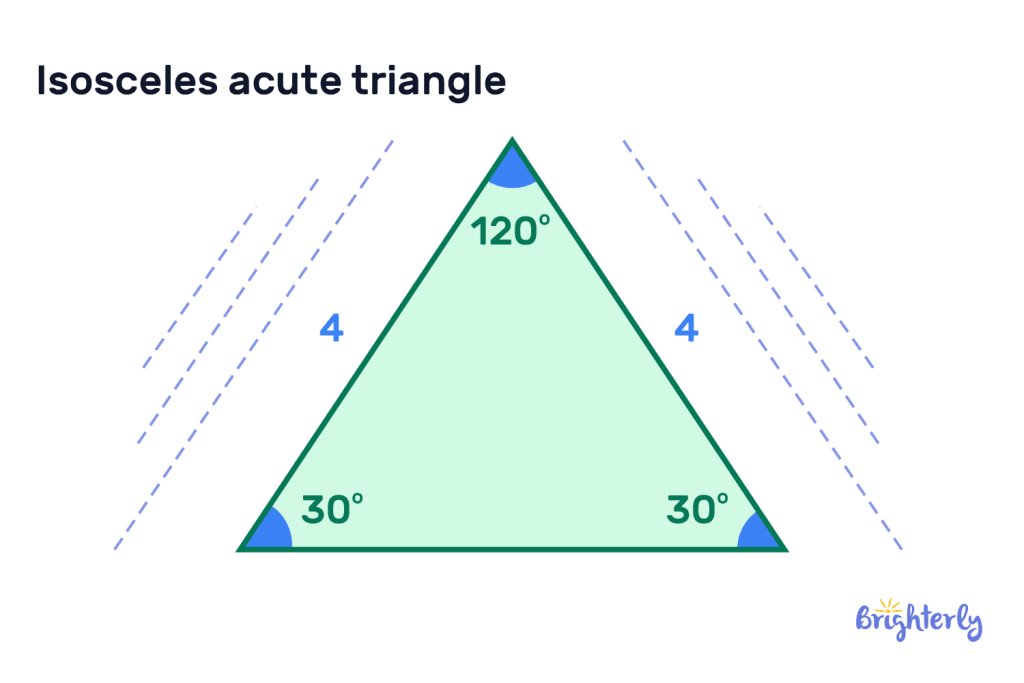
Isosceles acute triangle

In an isosceles acute triangle, two sides of the triangle will be equal length. This means the two angles opposite these equal sides are also equal.

Scalene acute triangle

In a scalene acute triangle, all three sides of the triangle are different lengths. This means that each internal angle will be different too – but they’ll still always be under 90°. Here is an acute scalene triangle example: 

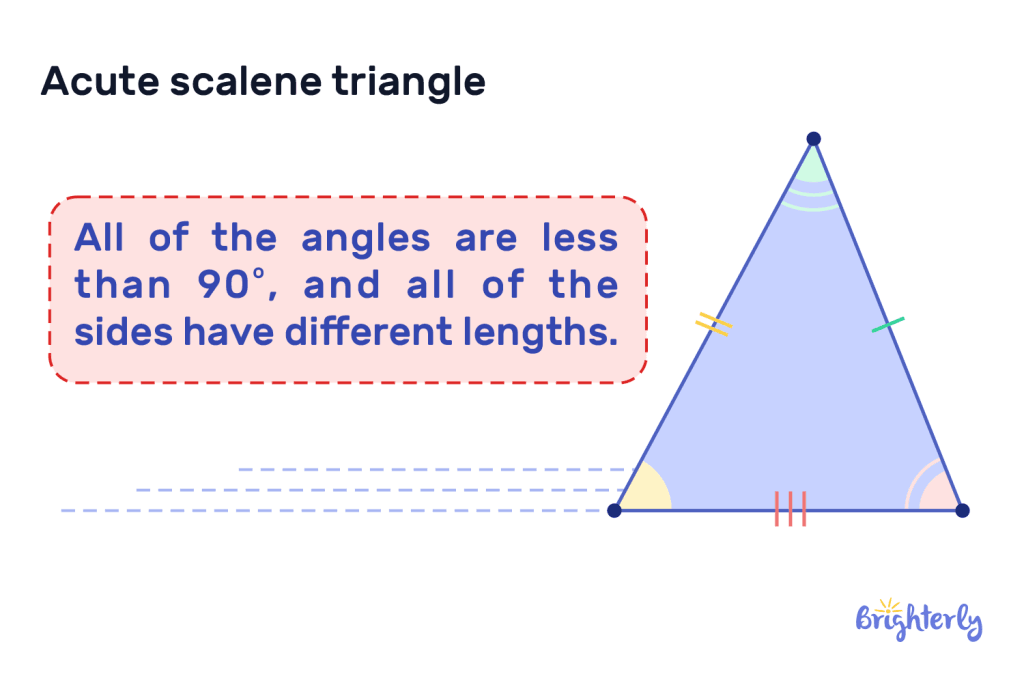
These are the main types of acute triangles, but there are some more specific classifications that are categorized by their side lengths and angle measures. 

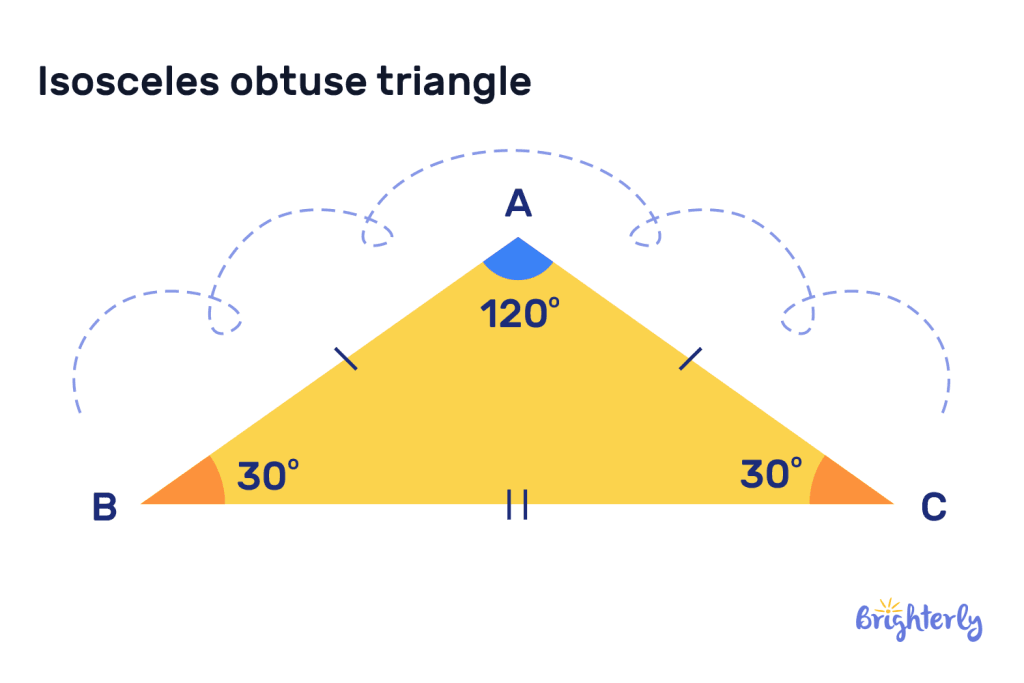
Obtuse-angled isosceles triangle

An obtuse-angled isosceles triangle will have one obtuse angle, which is an angle greater than 90° and two equal sides. Here is an acute and obtuse triangles example.

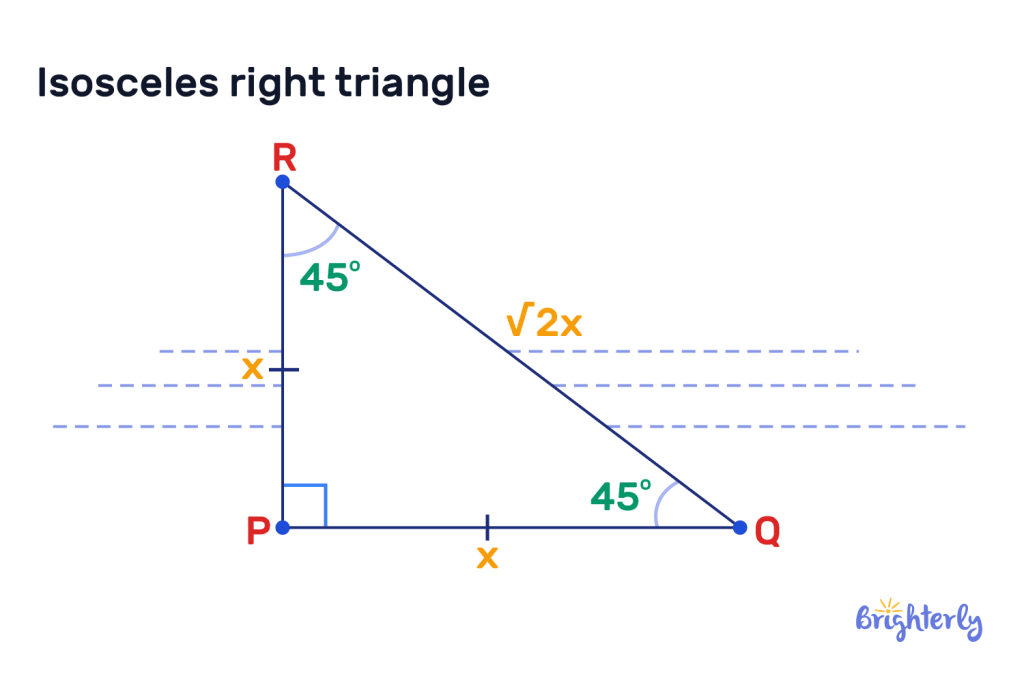
Right-angled isosceles triangle

The right-angled isosceles triangle has one right angle, which is 90°, and two equal sides.

Find out more about the different types of triangles with our informative article.

Acute triangle: formula

There are different formulas available that you can use to find the properties of acute triangles, including angle measures, area and side lengths. Here are the most common acute triangle formulas:

1. Law of cosines: a² = b² + c² – 2bc * cos(A)
2. Law of sines: a/sin(A) = b/sin(B) = c/sin(C)
3. Heron’s formula for area: Area = √(s * (s – a) * (s – b) * (s – c)), where s = (a + b + c) / 2 (semiperimeter)

Properties of acute triangle

The properties of acute triangles are factors that make them different to other types of triangles. 

• All acute triangles have angles of less than 90°.
• The sum of all acute triangle angles is always 180°.
• Acute triangles can also be equilateral, isosceles and scalene triangles.
• In an acute triangle, the shortest side is always opposite the smallest angle, and the longest side will always be opposite the largest angle.

Can an acute triangle be scalene?

Yes, an acute triangle can also be a scalene triangle. In scalene acute triangles, each of its three sides is a different length, meaning each angle is a different size too. An acute triangle real life example could be a slice of pizza.

Depending on their angle measurements, scalene triangles can be acute, right-angled or obtuse.

Math tutors

Improve your child’s math skill today with Brighterly

Let them be at the top of their class.

Book free lesson

Solved math tasks: examples

Now you know about acute triangles, why not put your knowledge to the test with our solved math tasks?

Which set of angles can form a triangle acutely?

Detail the angles that can form an acute triangle.

Answer:

Here are some examples of acute angles:

• 85°, 55°, 40°
• 60°, 70°, 50°
• 45, 35, 80°

What type of triangle has three acute angles?

Write down your answer.

Answer:

This is because acute triangles get their names from their acute angles, which are all below 90°.

How many acute angles are in an acute triangle?

Write down your answer.

Answer:

However, you can also have an acute right-angled triangle and an obtuse-angled acute triangle, which have two acute angles each.

Acute triangle: practice math problems

Acute triangle: worksheets

Put your new-found knowledge on acute triangles to the test with our free math worksheets!

• Classifying triangles worksheets
• Measuring angles worksheets
• Types of triangles worksheets
• Types of angles worksheets

Camille Ira B. Mendoza

21 articles

I am a seasoned math tutor with over seven years of experience in the field. Holding a Master’s Degree in Education, I take great joy in nurturing young math enthusiasts, regardless of their age, grade, and skill level. Beyond teaching, I am passionate about spending time with my family, reading, and watching movies. My background also includes knowledge in child psychology, which aids in delivering personalized and effective teaching strategies.