• Math tutors
• /
• Knowledge Base
• /
• y = mx + b – Definition, Slope-Intercept Form, Examples, Facts

y = mx + b – Definition, Slope-Intercept Form, Examples, Facts

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on October 22, 2024

Welcome to Brighterly, where we believe that math is not just a subject – it’s a magical language that helps us understand the world! 

We make even the most complex-looking math concepts look simple.

Today, we’re going to dive into an exciting concept that’s fundamental to algebra: the equation y = mx + b.

This equation is fundamental to creating line graphs and helps you express their properties in a simple way.

Here, we’ll cover the slope-intercept form y = mx + b, how to work out this equation, the y = mx + b meaning and how to find the slope of the equation. We’ll also provide you with some fun math worksheets and practice problems so you can further improve your knowledge!

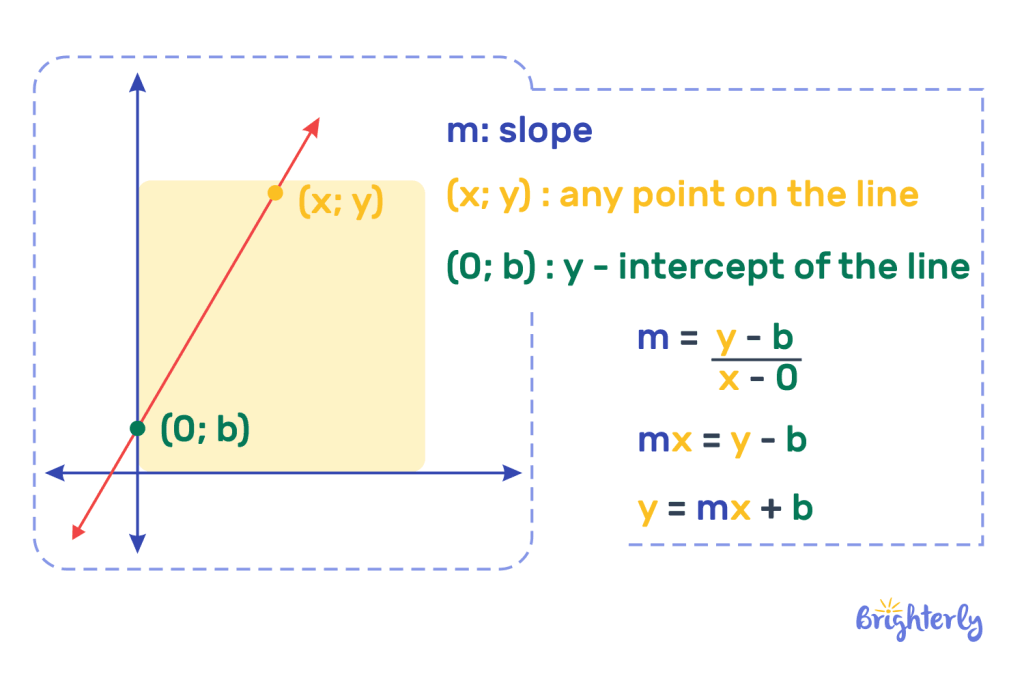
What is y = mx + b?

y = mx + b is a formula that’s also known as the slope-intercept form of a linear equation. But what exactly does that mean?

If we take a straight line on a graph, we must recognize that it has certain properties, including: 

• The slope, which represents how steep the line is
• The y-intercept, which represents where the line crosses the vertical y-axis, i.e. how far up the line goes (b in slope-intercept form)
• The x-intercept, which represents where the line crosses the horizontal x-axis, i.e. how far along the line goes

We can use the formula y = mx + b to help us describe these properties in a simple way. It’s important to know what each letter stands for in this equation.

What is m in y = mx + b?

m represents the slope of the line.

What is b in y = mx + b?

b represents the y-intercept.

What is x in y = mx + b?

x represents any value we pick along the x-axis (horizontal axis).

What is y in y = mx + b?

y represents the corresponding point on the line for our x value.

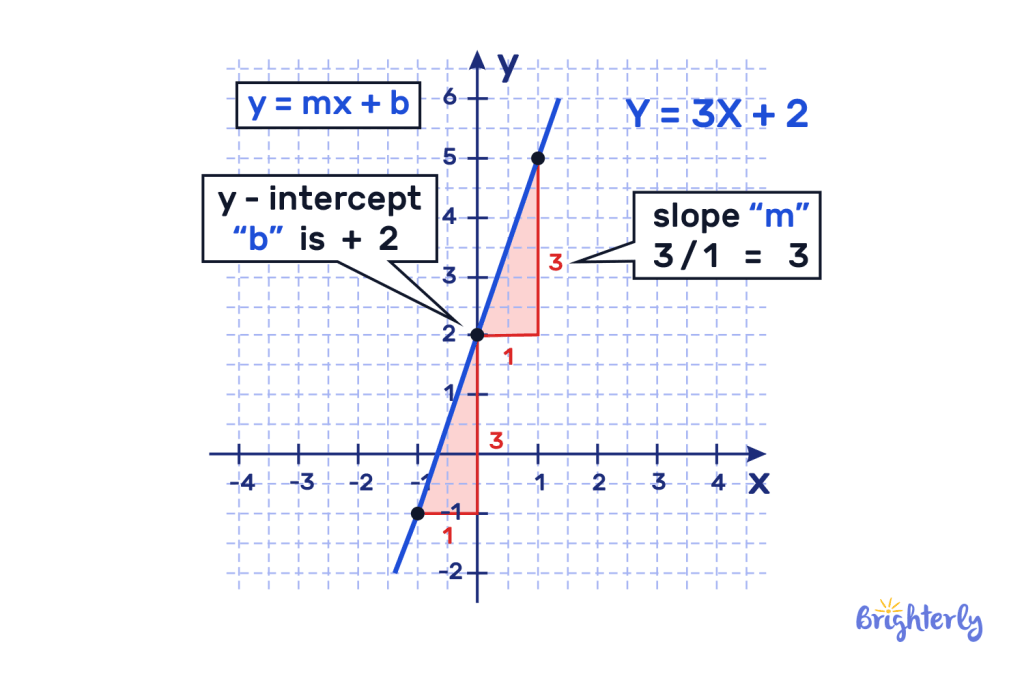
y = mx + b example

Let’s take a look at a y = mx + b equation example.

Below, you can see that the slope goes 1 place across and 3 up, which means m = 3 ÷ 1. This means m = 3.

The line intercepts the y-axis at the +2 point, which means y = 2. 

Therefore, our slope-intercept form is y = 3x + 2.

In all y = mx + b equations, you’ll notice that the y and the x always remain as variables, while our m and b variables are replaced by numbers.

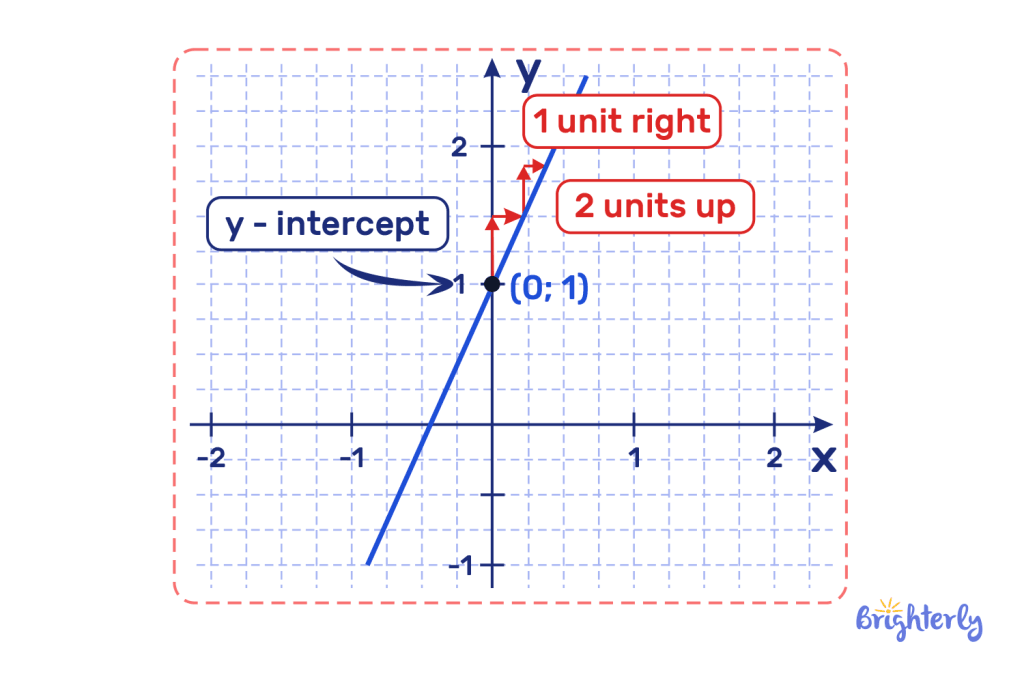
How to find y = mx + b?

y = mx + b might look intimidating, but it’s actually really easy! Once we know our slope (represented by m) and our y-intercept (represented by b), you simply use these figures in your equation, replacing those two variables with your numbers.

You’ll first need to calculate your slope, which is the rise (known as the vertical change) over the run (known as the horizontal change) between two points on a line. You’ll need to use the formula of m = rise ÷ run to find your slope. Then, once you know that number, you can swap it in for m in your formula.

Then, you’ll need to find the point where the line crosses the y-axis. This must be the point where it crosses this axis when x is 0. Once we have these two values, whether by identifying them on our graph or by given data, we can replace the m and b in our equation. You won’t replace the variables of y or x with numbers.

y = mx + b at origin

You might be wondering how we calculate y = mx + b when our line passes through the origin in our graph – AKA the point of 0,0. 

In this case, in y=mx+b, what is b? Our y-intercept b becomes 0 because that’s where our line intersects the y-axis – at the point of 0. 

Because of this, we can simplify our equation of y = mx + b to just y = mx.

This is a special case of the slope-intercept form, where the line directly passes through the origin, giving us a b value of 0.

How to find the slope of an equation y = mx + b?

To find the slope y = mx + b in your equation, you need to understand the difference in the x and y coordinates.

To work this out, you need to use the formula of m = rise ÷ run. This can also be expressed as m = (difference in y coordinates) ÷ (difference in x coordinates).

y = mx + b equations

There are some interesting facts you should know about y = mx + b equations that show how important they are to the world of mathematics and algebra. These facts and handy tips are:

• It’s the standard form used to describe any straight line in algebra
• When we talk about how steep a line is, we are referring to how steeply it rises or falls
• Positive slopes will move in an upward direction from left to right
• Negative slopes will move in a downward direction from right to left, meaning from left to right, they fall instead
• Lines with a zero slope or gradient are horizontal, with no rise or fall

Solved math tasks: examples

Now that you know everything there is to know about y = mx + b and how to use and solve it, try out our solved math tasks! Work them out for yourself, then check your answers to see how many you get right. You can always try again if you don’t get them quite right!

Solved math task 1

Let’s say you’re saving up for a new bicycle that costs $300. You already have $50, and each week you add $25 from your allowance to your savings. Express this as a linear equation.

Answer:

Here, the starting amount of $50 is your y-intercept (b).

The amount you save each week ($25) is your slope (m).

Therefore, if we let ‘x’ represent weeks and ‘y’ represent your total savings, the equation becomes y = 25x + 50.

Solved math task 2

Let’s imagine a company that sells cookies. It costs $100 to start up the business (buying ingredients, packaging, etc.) and each cookie costs $0.50 to make. Express this as a linear equation.

Answer:

The startup cost is the y-intercept (b = 100).

The cost per cookie is the slope (m = 0.5).

If ‘x’ represents the number of cookies and ‘y’ represents the total cost, our equation becomes y = 0.5x + 100.

y = mx + b: worksheets

Ready to test out and improve your knowledge of algebra, linear graphs and the equation y = mx + b? Try out our fun, free math worksheets with engaging puzzles and games – as well as learning, you’ll have plenty of fun!

• System of equations worksheets
• Graphing linear inequalities worksheets
• Graphing inequalities worksheets
• Algebra worksheets

Jessica Kaminski

67 articles

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.