Rational Numbers – Definition with Examples
reviewed by Jo-ann Caballes
Updated on October 3, 2024
Kids are introduced to rational numbers early in their math education, forming a fundamental basis for understanding fractions, decimals, and percentages. While learning to solve problems on rational in math, they deal with addition, subtraction, multiplication, and division.
But first, what are rational numbers? Here, we’ll define rational number in math, cover the main types of rational numbers, provide examples, and share practice test problems.
What is Rational Number?
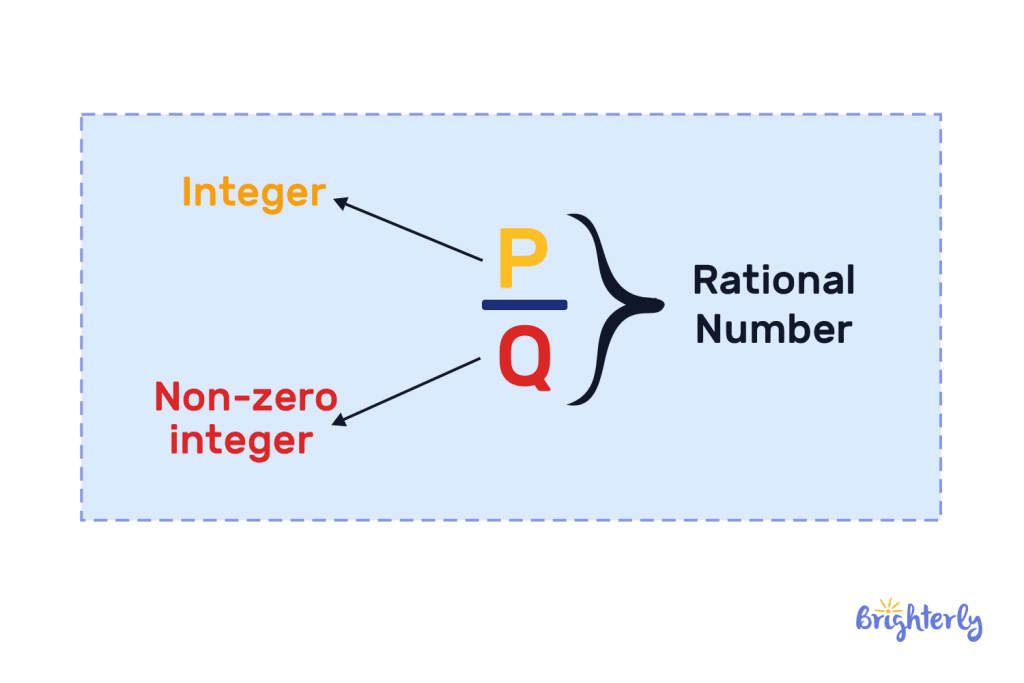
Rational Numbers are like fractions written as p/q, where p and q are whole numbers, and q is not zero. Simply put, if a fraction has a number on top and a number on the bottom that is not zero, it’s called a rational number.
Rational Numbers Definition
There are two major types of numbers: rational and irrational. We’ll cover the rational numbers definition and how they can be written as fractions. As you may have guessed, irrational numbers, on the other hand, cannot be written as simple fractions.
Rational numbers comprise two whole numbers: a numerator and a non-zero denominator. Everything in arithmetic can be related to rational numbers. For example, the number ½ is rational because it comprises two whole numbers, 1 and 2.

Set of Rational Numbers
For rational numbers, the top number (numerator) is a whole number, and the bottom number (denominator) is a whole number that isn’t zero.
Rational numbers can be positive, negative, or zero. For example, ⅓, -⅔, and 5/1 are rational numbers. Rational numbers are important in math because we use them a lot in everyday life.
Rational Numbers: Examples
Following what you now know of rational numbers, some examples include:
- ½
- -0.6667 or -⅔
- 10 or 10/1
- -6 or -6/1
- 5.0
- 0.8 or -8/10
- -0.2
Types of Rational Numbers
The different types of rational numbers are:
- Integers: Integers are just whole numbers. They can be positive rational numbers, like 4, or negative, like -5, and they can also be zero. You can think of them as numbers with no fractions or decimals. For example, 4 is the same as 4/1, and -5 is the same as -5/1. So, they are all rational numbers because you can write them as fractions.
- Fractions: Fractions are numbers like ⅖ and ⅓. The top part is called the numerator, and the bottom is called the denominator. Fractions are rational numbers as long as the bottom part (denominator) is not zero. They show how one number (the top) is divided by another (the bottom).
- Terminating Decimals: Terminating decimals are numbers that end after a few digits. For example, 0.12 stops after two digits. You can turn these numbers into fractions, too. For instance, 0.12 is the same as 12/100, which can be simplified to 3/25.
- Non-Terminating Repeating Decimals: These decimals go on forever but have a repeating pattern. For example, 0.333… keeps repeating 3 forever. These can also be written as fractions. For example, 0.333… is the same as ⅓.

How to Identify Rational Numbers?
The first thing to know about rational numbers is that:
- You can represent them as fractions and have their denominators be 1 (some examples are -4/1 and 9/1).
- As long as you have a fraction with a denominator greater than 0 and both denominator and numerator are whole numbers, you have a rational number. ⅝ is an example that fits this description.
- Numbers with digits after the decimal point, like 4.75, are rational and can be converted into fractions.
- Decimals that repeat a pattern forever, like 1.272727…, are also rational. They can be written as fractions.
- Decimals that go on forever without repeating are not rational. For example, √7 (about 2.645751…) is irrational because it never ends and doesn’t repeat.

Rational Numbers in Decimal Form
Rational numbers can appear as decimals in different ways: terminating and non-terminating decimals. Terminating decimals are numbers that end after a few digits. For example, 0.1 is a terminating decimal and can be written as the fraction 2/10. Non-terminating repeating decimals are numbers that go on forever but have a repeating pattern. For example, 0.333… repeats the 3 and can be written as ⅓.
List of Rational Numbers
There are so many rational numbers that we can’t list them all. For example, we can name a few, like 5, 2.5, ¾, -1, and 0.2. This list shows that rational numbers include natural numbers (like 1, 2, 3), whole numbers (like 0, 4), integers (like -3), fractions (like ⅖), and decimals that either end or repeat (like 0.666…). So, rational numbers are all the numbers you can write as fractions.
Examples of Rational Numbers
Here are some rational number examples:
- 3
- 4/9
- -⅝
Example 1: 3
The number 3 is rational because it can be written as a fraction. Think of it as 3 divided by 1. So, 3 is the same as 3/1. Since 3 can be written this way, it fits the rational number meaning, which are simply numbers that can be written as fractions with whole numbers on top and bottom.

Example 2: 4/9
The fraction 4/9 is a rational number because it is already a fraction. It means 4 divided by 9. Any number that can be written this way, with one whole number on top and another one on the bottom, is rational. So, 4/9 fits the definition of a rational number perfectly.
Example 3: -⅝
The fraction -⅝ is rational because it can be written as a fraction. Any number written this way is rational, with a whole number on top (the numerator) and another on the bottom (the denominator). So, -⅝ fits the definition of a rational number perfectly.
Adding and Subtracting Rational Numbers
When we add or subtract rational numbers, we use similar rules to regular numbers. Here are the steps for the subtraction of rational numbers:
Example: Solve ¾ – (-½)
Solution:
- Step 1: Addition is the easiest operation on rational numbers. So, change the subtraction to addition and flip the sign of the second fraction. So, ¾ – (-½) becomes ¾ + ½ .
- Step 2: Add these fractions. To do that, find a common denominator. Here, the common denominator for 4 and 2 is 4. Get the equivalent fractions of the numerators. This equation becomes ¾ + ¼.
- Step 3: Now add ¾ and 2/4. That gives 5/4 or 1¼.

Multiplying and Dividing Rational Numbers
To multiply rational numbers, just multiply the top numbers (numerators) together and the bottom numbers (denominators) together.
Example: Multiply ⅔ by 4/5
Solution:
- Step 1: Multiply the top numbers: 2 x 4 = 8
- Step 2: Multiply the bottom numbers: 3 x 5 = 15
- Step 3: So, ⅔ x ⅘ is 8/15.
To divide rational numbers, change the division to multiplication by flipping the second fraction (finding the reciprocal).
Example: Divide ¾ by ⅖.
Solution:
- Step 1: Flip the second fraction: ⅖ becomes 5/2.
- Step 2: Multiply ¾ by 5/2.
- Step 3: Multiply the numerators, so 3 x 5 = 15.
- Step 4: Multiply the denominators, so 4 x 2 = 8.
- Step 5: ¾ ÷ ⅖ = 15/8.
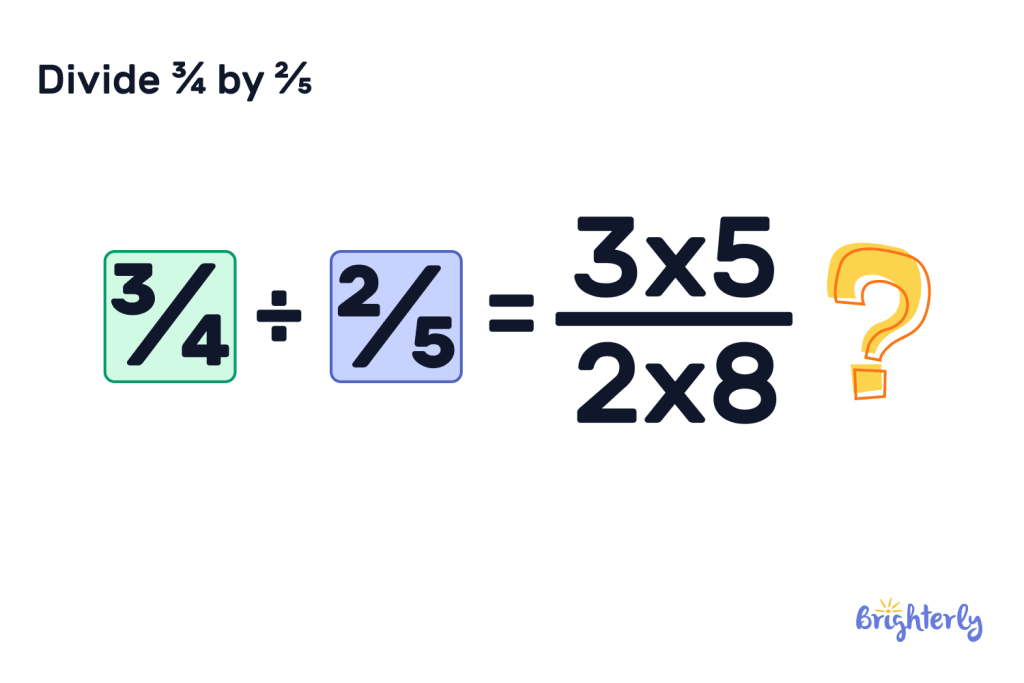
Rational and Irrational Numbers
Rational numbers can be written as fractions, where both the top number (numerator) and the bottom number (denominator) are integers, and the denominator is not zero. For example, ⅔ is a rational number because it fits this rule. Rational numbers include positive numbers, negative numbers, and zero.
The difference between rational numbers and irrational numbers is that the latter cannot be written as simple fractions, expressed as a ratio of two integers, or have decimal expansions that go on forever without repeating. For example, √2 is irrational because it cannot be expressed as a fraction, and its decimal form does not terminate or repeat.

Solved Math Tasks: Examples
Example 1: Express 18/30 in standard form
Solution:
- Step 1: Find the greatest number to divide 18 and 30 without leaving a remainder. This number is 6.
- Step 2: Divide the numerator (18) and the denominator (30) by 6. 18 ÷ 6/ 30 ÷ 6 = ⅗.
| So, 18/30 in standard form is ⅗. |
Example 2: Add ⅔ and 4/9.
Solution:
- Step 1: Find a common denominator for both fractions. 9 is the least common multiple of 3 and 9.
- Step 2: When converting a rational number, both fractions after having 9 as the denominator. So, we have 9 (the common denominator) divided by 3 (the denominator) multiplied by 2 (the numerator). The outcome is 6. Thus, the new fraction is 6/9.
- Step 3: Add the fractions. 6/9 + 4/9 = 10/9.
| So, ⅔ + 4/9 is 10/9 or 1 1/9. |
Example 3: Subtract ⅖ from 7/8.
Solution:
- Step 1: Find a common denominator for both fractions. The least common multiple of 5 and 8 is 40.
- Step 2: Convert both fractions after having 40 as the denominator. So, we have 40 (the common denominator) divided by 5 (the denominator) multiplied by 2 (the numerator). The outcome is 16. Thus, the new fraction is 16/40.
- Step 3: Do something similar for the other fraction. So, we have 40 (the common denominator) divided by 8 (the denominator) multiplied by 5 (the numerator). The outcome is 35. Thus, the new fraction is 35/40.
- Step 4: Subtract the fractions. 35/40 – 19/40. The denominator is the same, so you pick one. The answer becomes 19/40.
| So, when you subtract ⅖ from ⅞, you get 19/40. |
Rational Numbers: Practice Math Problems
Rational Numbers Worksheets
Now that you know the definition of rational numbers in math, you should check out these Brighterly’s worksheets to improve your children’s interest in math and their ability to coast through common math problems.