• Math tutors
• /
• Knowledge Base
• /
• Addition: Definition, Properties, and Examples

Addition: Definition, Properties, and Examples

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on December 19, 2024

Addition is the first arithmetic operation children learn when discovering about the relationship between numbers and quantities. After which, they can proceed to learn other operations such as subtraction, multiplication, and division.

In this Brighterly article, we learn the addition definition, go through practice problems, recommend relevant worksheets, and even share tips on how you can teach youngsters to do addition.

Let’s get started.

What is addition?

Addition is the combination of two or more quantities. We use addition to find the new value of two or more numbers or amounts.

Addition is often the first of the four basic arithmetic operations we learn when we begin our lifelong journey in mathematics. The other three are subtraction, multiplication, and division.

What makes addition special is that it is an essential operation that we can barely go a day without performing — we use it for everything from counting money to calculating time, and so on. 

Definition of addition 

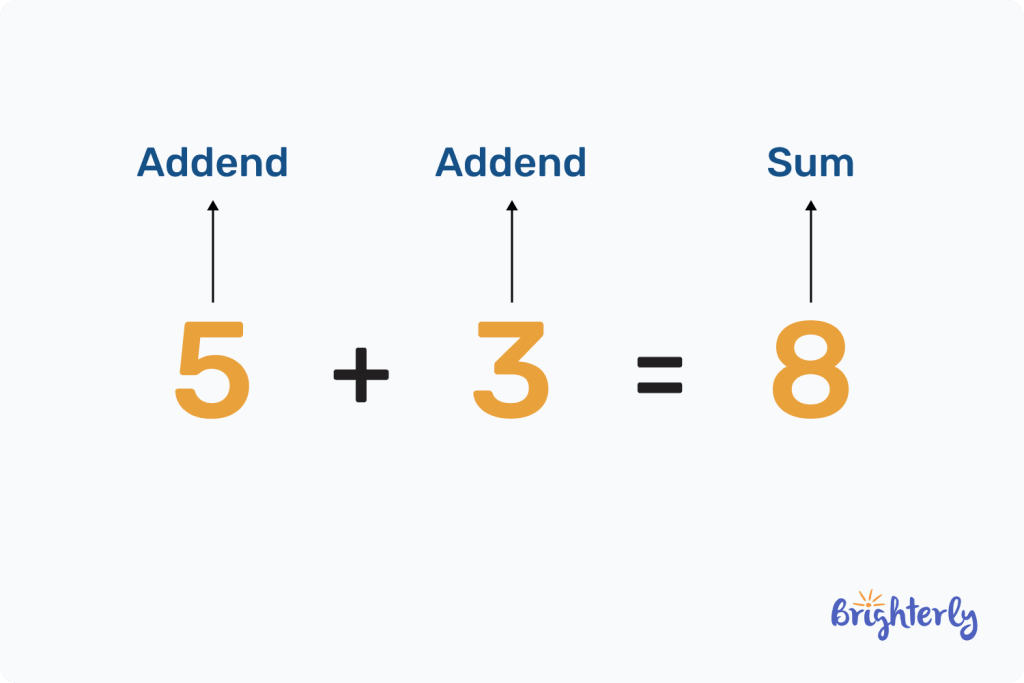
We may define addition as the mathematical operation of putting two or more numbers together which results in a new number. The result of addition is known as a sum. The numbers that make up the sum are called addends.

Addition symbol

The addition symbol is “ + ”. This symbol is also referred to as the plus sign and when we want to read addition equations we use plus, such as 3 + 4 = 7 is an addition sentence of 3 plus 4 equals 7. But what is an addition sentence?

What is an addition sentence?

An addition sentence is the manifestation of the addition formula.  It shows how the sum is addition result. The sum is gotten by combining two or more numbers.

Thus, 5 + 3 = 8 is an addition sentence.

Addition Formula 

The formula of addition is:

Addend + Addend = Sum.

According to addition terminology,  addends are numbers accumulated to form a new number. This new number is the answer to an addition problem which is called the sum. Per the formula, if a, b, and c are real numbers then, a + b = c.

How to teach addition to kids

When introduced to the concept of addition, most kids already have questions ready, like “What is the answer to an addition problem called?”. This is why even though most grownups are very familiar with addition, teaching it can be entirely different. Here are some tips to help you teach addition: 

• Explain the addition meaning and coin a basic addition definition for kids like the one we use in this article
• Make examples from objects, toys, and real-life situations
• Train them on basic addition facts such as 2 + 2 = 4, 5 + 5 = 10, etc.
• Encourage them to practice on their own.

Addition examples

Here are some more examples of additions to help you get the hang of it:

Imagine we had 4 oranges and 6 mangoes, to find the total sum of fruits, we can express it as:

4 + 6 = 10.

Another example of addition in action is the total sum of paintings in a room when there are 12 paintings on the right wall and 6 on the left wall.

We express this as 12 + 6 = 18.

In this example 12 and 6 are the addends and the sum (the result of adding two or more numbers) is 18.

How to add: Ways to solve addition problem

There are various ways to approach and solve addition problems. Let’s go over some of them:

Addition steps using fingers

We do addition so often and suddenly that we have a method of adding 2 numbers with our fingers. However, since our fingers are only up to 10, this method of addition is limited to smaller numbers.

Here are the addition steps to finding the sum of numbers with our fingers:

• Step 1: Count the first numbers by extending the fingers of one hand 
• Step 2: Count the second number by extending the fingers of the other hand.
• Step 2: Count all the outstretched fingers together. That’s the total sum.

For example, if we were to add 3 + 4, we can do this simple addition with our fingers, we first count and extend 3 fingers on one hand and 4 fingers on the other hand. Finally, we count all our extended fingers which gives us 7.

Addition steps using the number line

We can also do math addition with a number line. A number line is a horizontal line, marked with 0 in the middle. It contains positive numbers extending infinitely to the right and negative numbers extending infinitely to the left.

Using a number line is particularly helpful for visualizing addition to see how it works in real time. Here are the steps on how to use a number line for addition:

• Step 1: Highlight one of the addends in the number line (it is best to highlight the bigger number)
• Step 2: Move towards the right. The amount of times you move is the second addend.
• Step 3: Highlight the number which you land upon. This is the sum of both numbers.

For instance, if we are to find the sum of 4 + 8 with a number line, we first draw the number line and highlight 8, next we move towards the right, 4 times (if we highlighted 8, we’d move rightwards 8 times), the number we end up on is the sum, here, it will be 12.

Addition steps using the number grid

A number grid, also known as a number chart, is another method we use to calculate addition in math. A number grid is a table of rows and columns containing a number in each cell — these numbers are arranged sequentially, starting from “1” at the top left corner.

Here are the steps to add numbers using a number grid:

Step 1: Highlight the first addend on the number grid (it’s best to start with a bigger number).

Step 2: Move rightwards the same number of times as the second number 

Step 3: The number we land on is the sum.

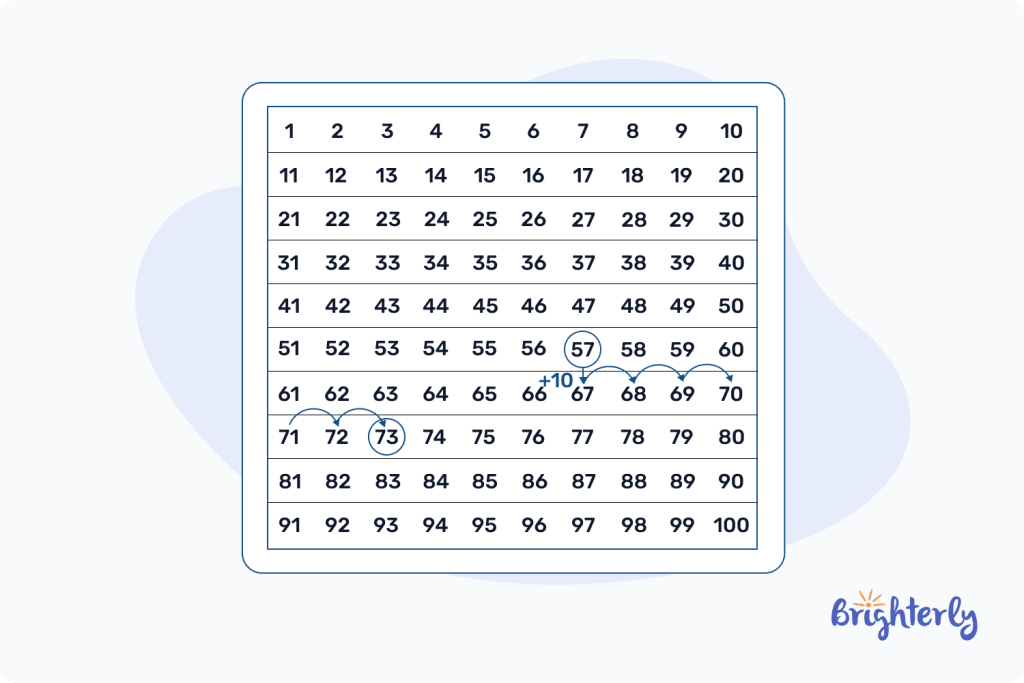
When the addition is done for numbers with a difference of more than 10, we can simply go down the column for a plus 10 and move rightward for the rest of the number that is less than 10.

Addition steps by counting forward

Another way to do addition is by simply counting forward. Here is how it works in steps for 6 + 3:

• Step 1: Start with the bigger number. In this case, it’s 6.
• Step 2: We count forward as many times as the second number, i.e., 3 times. The counting goes thus; 7, 8, 9.
• Step 3: We identify 9 as the sum of 6 and 3.

Vertical Addition

Addition problems can be solved by arranging the numbers in a vertical order. This order includes arranging the numbers according to their place values, i.e., ones, tens, hundreds, thousands, etc.

We begin addition from the ones in the rightmost place, then the tens, and so on. When we add numbers with this method, we may have to regroup.

Regrouping in Addition

Regrouping is a concept that occurs in both addition and subtraction. We use regrouping when the sum of two digits results in a number greater than or equal to 10. This will affect the calculation, therefore, we regroup by adding the “excess” to the next place value. 

Regrouping for addition is also known as “carrying over”.

Addition without Regrouping

With the vertical method, we don’t always have to regroup when we find the answer to an addition problem. There are some ties when we can add the numbers without carrying over any excess.

For example, if we were to solve the equation; 62 + 34:

6 2

+ 34

96

In this example, here are the steps we followed:

Step 1: We arranged the numbers vertically on top of each other according to their place values. 

Step 2: We start addition from the rightmost numbers.

Step 3: The sum is the number at the bottom.

Therefore, 62 + 34 = 96.

We do not have to regroup here, because the resulting digits can fit into their place values.

Addition with Regrouping

In the cases that demand that we regroup in addition, the resulting sum from the digits must be above 9. 

Let’s look at an example:

For the equation,  37 + 14, regrouping will be used. Here’s how:

• Step 1: Arrange the numbers in vertical order on top of each other from ones to tens

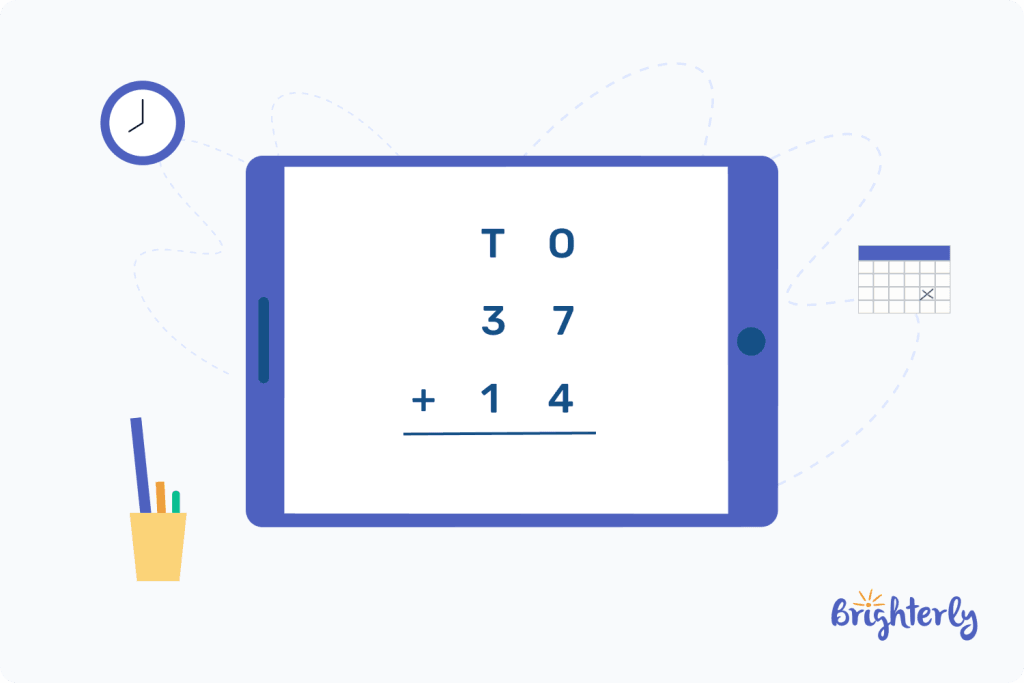
• Step 2: Begin addition from the rightmost part (7 + 4 = 11). Because the sum is a two-digit number, we need to carry over the tens place value of the digit to the next number. Here, the digit in the tens place value is 1. 

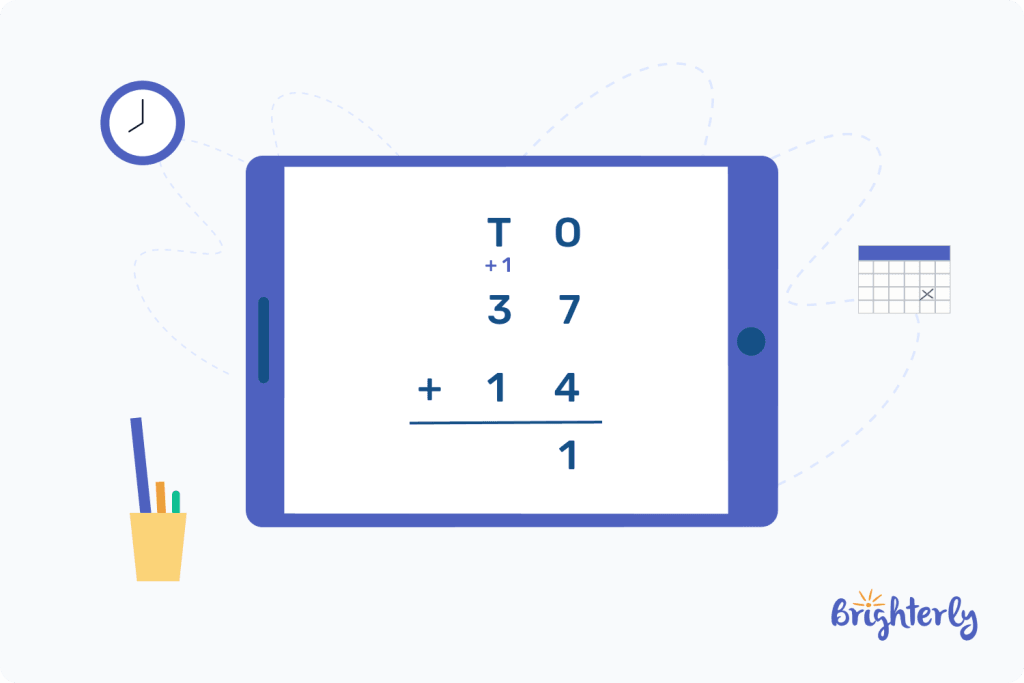
• Step 3: Add the “carry over digit” (1) to the other number (3), then add the result with the other digit below (3 + 1 + 1 = 5)

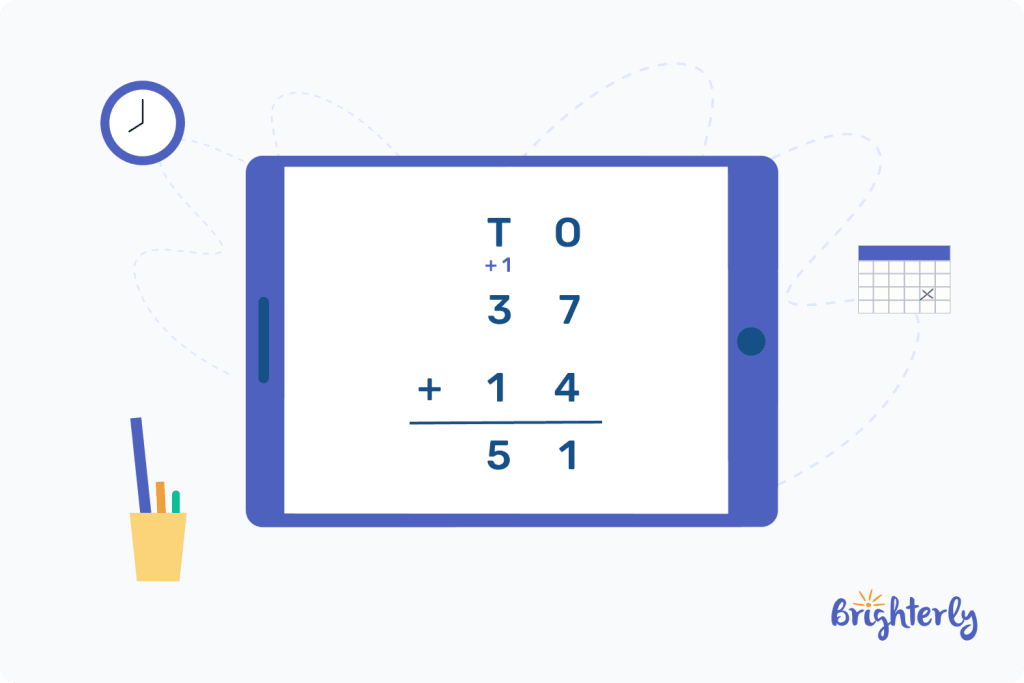
Therefore, the sum of 37 + 14 is 51.

Note that regrouping does not apply to the first digits or the leftmost digits in the vertical order arrangement.

For example, if we are to add 81 + 22,

8 1

+ 2 2

103

Since there is no other place to carry over to, we simply write the number as is.

Math tutors

Find the homework support your child needs!

Top math tutors for elementary and middle school students here.

Begin with a demo lesson

Properties of Addition

Addition has a set of principles that guide how we approach any problem involving the operation. They are:

• Commutative property of addition: This principle states that regardless of how we arrange the numbers involved in addition, the result stays the same. For instance, 13 + 21 = 34 is the same as 21 + 13 = 34. In both instances, the sum is still 40, despite switching the order of the numbers.
• Additive identity property of addition: In math, adding any number to 0 means the sum is the number. This means 0 does not alter the value of that number. To grasp this property better, imagine you picked 5 flowers from a garden and a friend gives you 0 flowers, the total amount of flowers you have remains 5 (5 + 0 = 5).
• Distributive property of addition: This property is the rule that if a, b, and c are natural numbers, a x (b + c) = (a x b) + (a x c).

For example 2 x (3 + 4) = (2 x 3) + (2 x 4)

= (6) + (8)

= 14.

This property shows us that we can expand our equation by multiplying one number by the sum of other numbers. 

• Associative property of addition: The sum of a group of numbers is consistent whether or not we alter the grouping arrangement. For instance, 32 + (11 + 9) = 52. This is the same answer we get when we solve it as 11 + (32 + 9) = 52.

Solved Examples on Addition

Solved Math problem 1

Phil uses 3 eggs to bake, his mother uses 5 eggs to make scrambled eggs and his brother makes hardboiled eggs with 2. How many eggs did Phil and his family use in total? 

Solution

3 + 5 + 2 = 10. 

Solved Math problem 2

With the use of a number line, add 7 + 5

Solution

First, we start with 7 and then move towards the right 5 times.

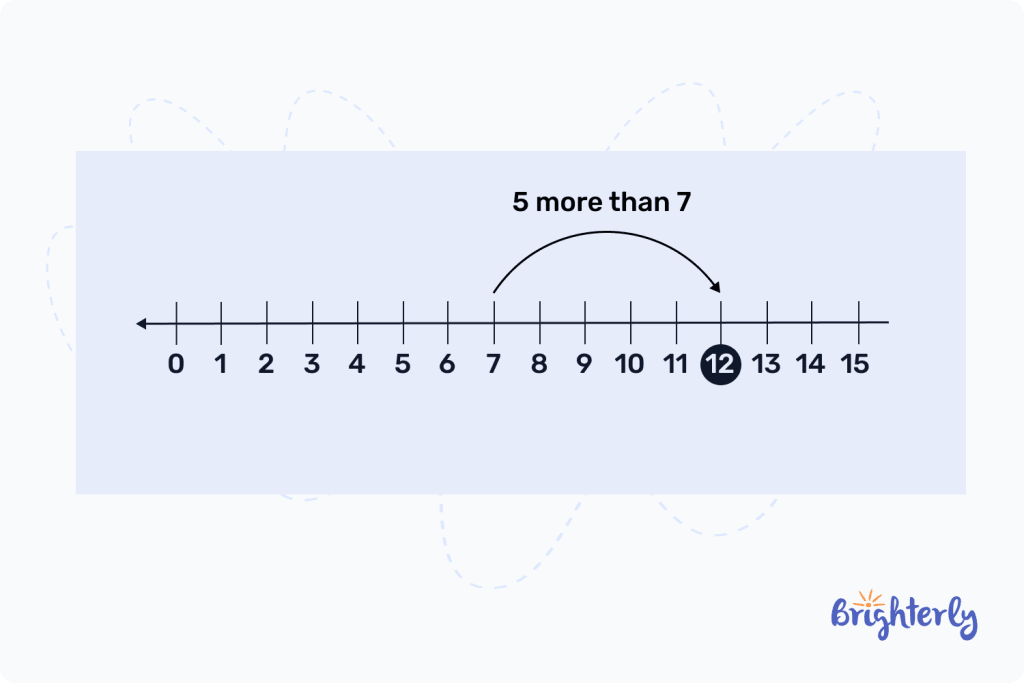
We land on 12, therefore, 7 + 5 = 12.

Solved Math problem 3

Find the total value of these fractions:

2/5 + 7/5 + 8/5

Solution

2 + 7 + 8 =  17.

Since the denominators of the fractions are the same (5), we don’t add them, so, 2/5 + 7/5 + 8/5

Solved Math problem 4

Mae and her friends go grocery shopping. They buy a gallon of milk for $3.50, loaves of bread for $7.20, cheese for $6, and sugar for $8.12. Calculate the total amount they spent with the vertical order.

Solution

First, we arrange all the money spent:

3 . 50

7 . 20

6 . 00

8  . 12 

24 . 82   

Therefore, Mae and her friends have spent $24.82 on grocery shopping.

Practice Problems on Addition

Addition: Recommended Worksheets 

The expert tutors at Brighterly have put together some free worksheets to help math learners understand addition better:

• Addition worksheets 
• Addition word problem worksheets 
• Addition and subtraction worksheets 

Jessica Kaminski

72 articles

Jessica is a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.