Base Ten Numerals – Definition with Examples
reviewed by Jo-ann Caballes
Updated on November 28, 2024
Welcome to Brighterly, the home of easy math learning!
Today, we’re covering a fundamental concept in math: the base ten numeral system.
We’ll cover what is base 10, the base 10 meaning, the value chart, how to find the place value of a digit and how to show base 10. We’ll also share practice test problems and puzzle-based worksheets so you can practice your learning!
What are base ten numerals?
Base ten numerals are a core concept in math. It’s the system of numbers we work with on a daily basis and forms part of the positional notation field. We cover the full definition of base ten numeral form below.
Base ten numerals definition
The definition of base ten numerals is the number system we use daily. The base 10 numerals are 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. The base ten numbers system is made up of numbers that are a combination of these 10 digits. Each digit’s place in the system denotes its value, which is where the positional notation comes in. Every digit in a number has a value to the power of 10.
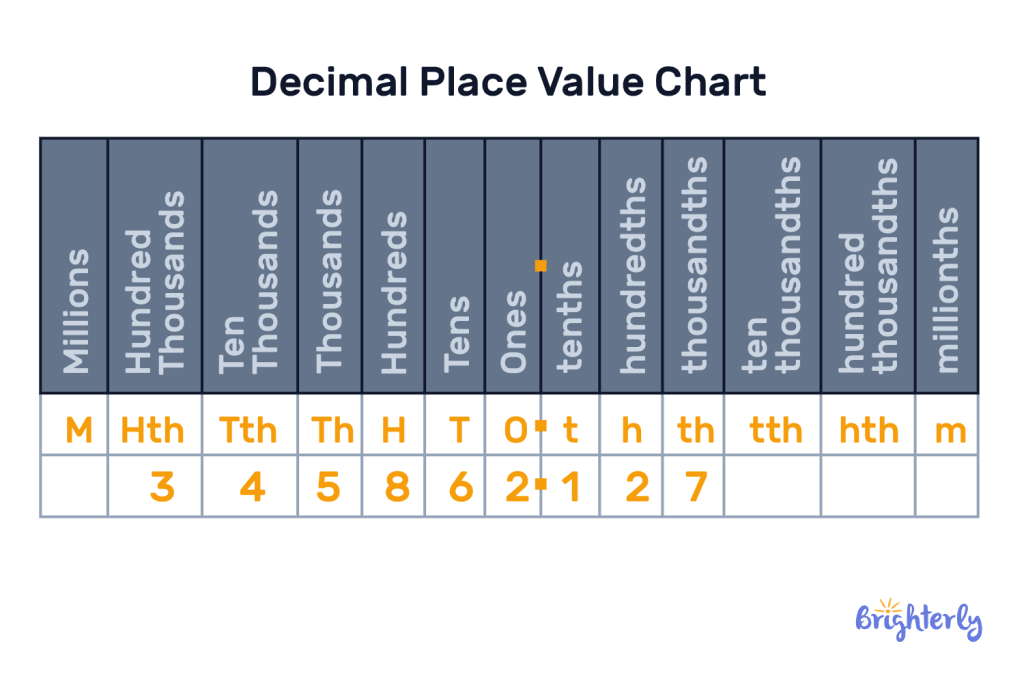
Base-ten place value chart
In the base-ten place value chart, you’ll see each digit in its position in your number and how that decides its value. The digit on your right-hand side is in the one’s place, then for each digit to the left, its value is ten times larger. The second place is tens, the third place is hundreds, the fourth place is thousands, and so on.
Here’s the base 10 chart:
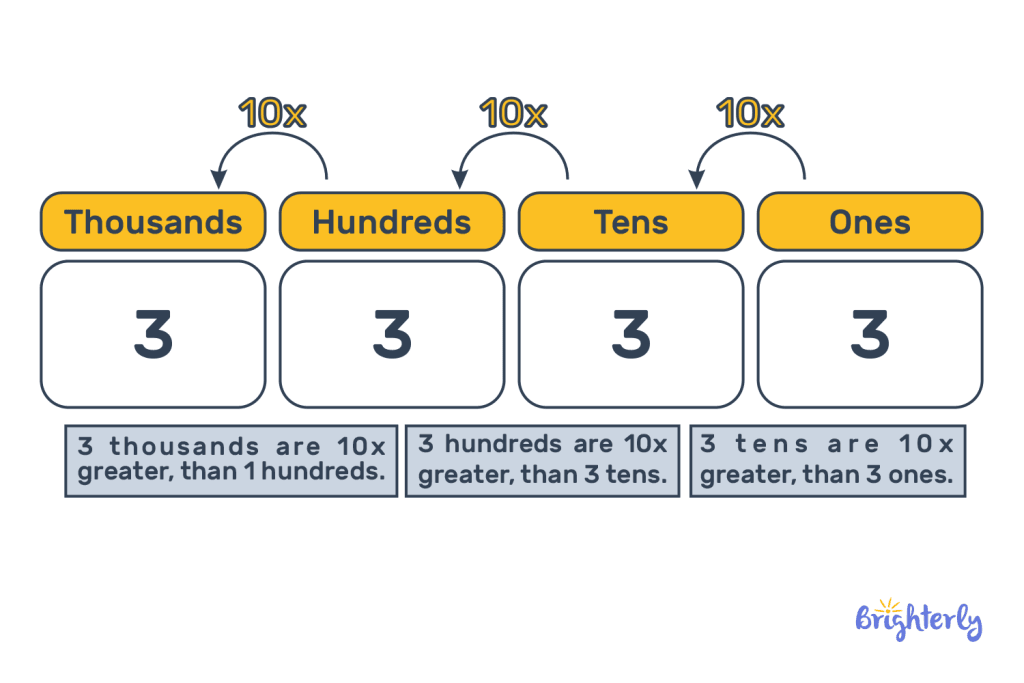
Base 10 form example
Let’s use a base ten numerals example. If we take 2435, we can break it down as follows in the base 10 number system:
- 2000 (2 thousands)
- 400 (4 hundreds)
- 30 (3 tens)
- 5 (5 ones)
How to find the place value of a digit?
To find the place value of a digit, you’ll need to count its position from the right. If it’s the first digit on your right-hand side, it’s in the one-place value. Next to the left, you have the tens place value, then the hundreds, thousands, ten-thousands, etc.
Base-10 (decimal number system)
The base-10 decimal number system expresses numbers in positional notation. This means digit values (aka column values) are represented in powers of 10. It’s one of the most foundational concepts in math and is essential to learning to understand more complex concepts.
Numbers in decimal number system
The numbers in the decimal number system are the same as in the base 10 system because decimal system is another name for the base 10 numerals system. Numbers 0-9 are used in this system and a number can be a combination of any of these digits.
Base of a number system
The base number of a system refers to how many unique digits can be used as part of that system. In the system, any combination of these numbers can be used. In the base 10 numeral system, the base is 10, so we can create numbers using 10 digits (0 to 9).
How to show the base-ten?
To show the base-ten, you can write your number out, ensuring that each digit is in the correct place number. This is because the decimal system is widely used and therefore this is widely understood. You can also use subscript notation – i.e. we would display 6537 as 6537_(10) in base-ten.
Expanded form
In base-ten numerals, expanded form is when we display each digit of our number multiplied by its place value. Let’s take the base ten model example of 4653: its expanded form is 4000 + 600 + 50 + 3. The expanded form can make large and complex numbers like this easier to work with in sums.
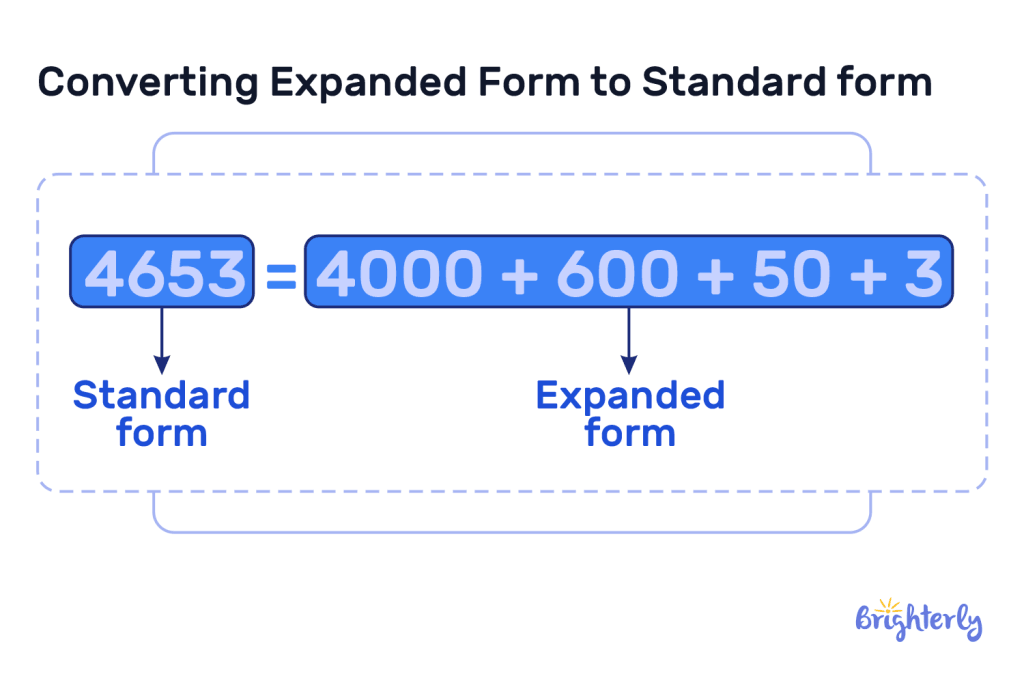
Place values in decimals
The base ten system also works with decimals, not just whole numbers. They move to the right of the decimal place and decrease by the power of 10. The first digit after our decimal point represents tenths (1/10), followed by hundredths (1/100), with each number representing one-tenth of the previous place value.
Solved examples on base-ten
Ready to put your knowledge to the test? Try out our solved math puzzles, then check your answers!
Solved example 1
Represent the number 2356.78 in its expanded form.
Answer:
| 2000 + 300 + 50 + 6 + 0.7 + 0.08. |
Solved example 2
Represent the number 4096 in its expanded form.
Answer:
4000 + 90 + 6.
| There is no digit in the hundreds place. |
Practice questions on base-ten
Here are some more base ten test questions for you to practice on!
- Write the number 628 in expanded form.
- 600 + 20 + 8
- What is the place value of the digit 3 in the number 3456?
- The hundreds place
- Write the number 9876.543 in expanded form.
- 9000 + 800 + 70 + 6 + 0.5 + 0.04 + 0.003
- What is the place value of the digit 8 in the number 0.789?
- The hundredths
- Write the base-ten number for 60+3
- 63
Base-ten numeral: practice math problems
Base-ten numeral: worksheets
Hone your learning on base-ten numerals with our puzzle-filled math worksheets!
Frequently asked questions on base-ten
Why do we use base-ten?
We use base ten because it’s widely and commonly understood. It’s the most simple way to represent numbers and is understood around the world.
What is the significance of base-ten in real life?
The significance of base ten in real life is that it underpins all math concepts and operations. We use base-ten for everything from counting to measuring. It also forms the basis for our key math operations of addition, subtraction, multiplication and division.
How is base-ten related to place value?
Base ten relates to place value because it defines the numbers that we can use in each place value. For every place to the left, the digit is multiplied by the power of 10.
What’s the difference between base-ten and other number systems?
The difference between base-ten and other number systems is the bases they use. In other words, they represent numbers with different numbers of digits or symbols. The base-ten system is the most widely recognized because it uses all available single-digit numbers.
Online Winter Math Camp for Grades 1-8
Join us to help your kid achieve their full math potential.
Choose kid's grade
Online Winter Math Camp for Grades 1-8
Join our Math Winter Camp and boost your child's math skills with our best tutors.
