• Math tutors
• /
• Knowledge Base
• /
• Expression in Math – Definition with Examples

Expression in Math – Definition with Examples

Camille Ira B. Mendoza

reviewed by Jo-ann Caballes

Updated on October 8, 2024

We’re committed to making even the most seemingly complex mathematical concepts easy and enjoyable to learn at Brighterly.

Today, we’ll be covering mathematical expressions – the building blocks to more complex math concepts and an essential element of your math education.

In this article, we’ll cover the expression definition in math, its elements, different types of expressions and the distinction between expressions and equations. We’ll also define algebraic expression in math and share expression examples and practice math problems to help you cement your learning!

What is an expression in math?

In math, an expression is the combination of numbers, variables and mathematical operators (your core operations of addition, subtraction, multiplication and division). These factors combine to represent a mathematical relationship. 

Mathematical expressions are often used in the real world, and they’re essential to learn before you move on to more complex mathematical concepts like functions and equations.

Expression in math: definition

The definition of an expression in math is a sum or calculation that represents the relationship between variables, numbers and operators. They allow us to express complex math ideas in a form that’s easy to understand and digest.

Examples of expression in math

An example of an expression in math would be 3x + 2. This represents the relationship between the variable x and a combination of numbers and operators.

Parts of an expression in math

You’ll need to be familiar with the parts of an expression in math to truly understand how it operates. A mathematical expression can have 4 parts:

1. Constants
2. Variables
3. Terms
4. Operators 

We cover each part below.

Constants

The constant is the part of the expression that will never change. They will only ever involve numbers. This value is always the same, and is always definite, and nothing in the expression can change it.

To illustrate the constant, think about the shoes you’re wearing. They’ll never change in size, so in an equation, your shoe size will always be a constant.

Variables

Variables are where we get algebraic. Variables will be represented by letters that show a part of the equation that may change or be unknown. If we take 3x + 2 as an example again, this means 3 something plus 2 – the something may be unknown, which is why it isn’t represented with a number. This is the variable expression definition.

Terms 

Terms in an expression can be numbers, variables, a product of a variable and a number or the product of multiple variables. A term is essentially every individual element that makes up your expression, except for your operators. Expressions can be made up from a single term or multiple terms.

In our example of expression, 3x + 2, 3x and 2 are both terms.

Operators

The operator represents mathematical operations in your  mathematical expression. These can be addition (+), subtraction (-), multiplication (×), and division (÷).

In our example of 3x + 2, + is the operator because it’s instructing you to add 3x to 2.

Math tutors

Join Brighterly for personalized lessons for your child

Meet the best tutors for interactive math learning.

Book free lesson

What is distributive property in math?

The distributive property in math refers to a number that’ll multiply terms in your expression. It’s represented by a number that suits outside a pair of brackets to represent that both numbers should be multiplied by this number.

The simple distributive property equation is represented as A(B + C) = AB + AC.

Anything that is inside the brackets is multiplied by the number outside the brackets, which is your distributive property. By solving this part of your expression or equation, you can simplify it.

Expression in math: types

Did you know that there is more than one type of expression in math? The types of expressions are:

1. Numerical expressions
2. Algebraic expressions
3. Polynomial expressions

Numerical expressions

Numerical expressions will only contain numbers and operators. They may look like a simple or a more complex sum.

For example, both 4 + 7 and 3 x (5 – 2) are numerical expressions.

Algebraic expressions

Algebraic expressions are the next step up from numerical expressions. The algebraic expression meaning is an expression that can contain variables (represented by letters), numbers and operators.

Let’s use an algebraic expression definition and example: both 3x + 2 and y x (x – 7) are algebraic operations.

Polynomial expressions

Polynomial expressions are a specific type of algebraic expression. In a polynomial expression, your variables have whole number exponents (numbers to the power of another number) and are combined using an operation – addition, subtraction or multiplication.

For example, both 4×2 – 3x + 1 and 5y3 – 2y2 + 7y are polynomial expressions.

Simplifying expressions in math

By simplifying an expression in math, you can make it easier to read, understand and work with. Simplifying an expression involves combining like terms, factoring or using your properties of operation – like the distributive property that we’ve just discussed. 

Let’s use an expression example. Say we have the following expression: 4 x + 2 x – 3y + y.

To find the expression in its simplest form, first you would combine the like terms: 4x and 2x are like terms because they represent the same variable, so you combine them to get 6x.

Then, you’d combine the like terms of -3y and y to get -2y.

Therefore, your final simplified mathematical expression is 6x – 2y.

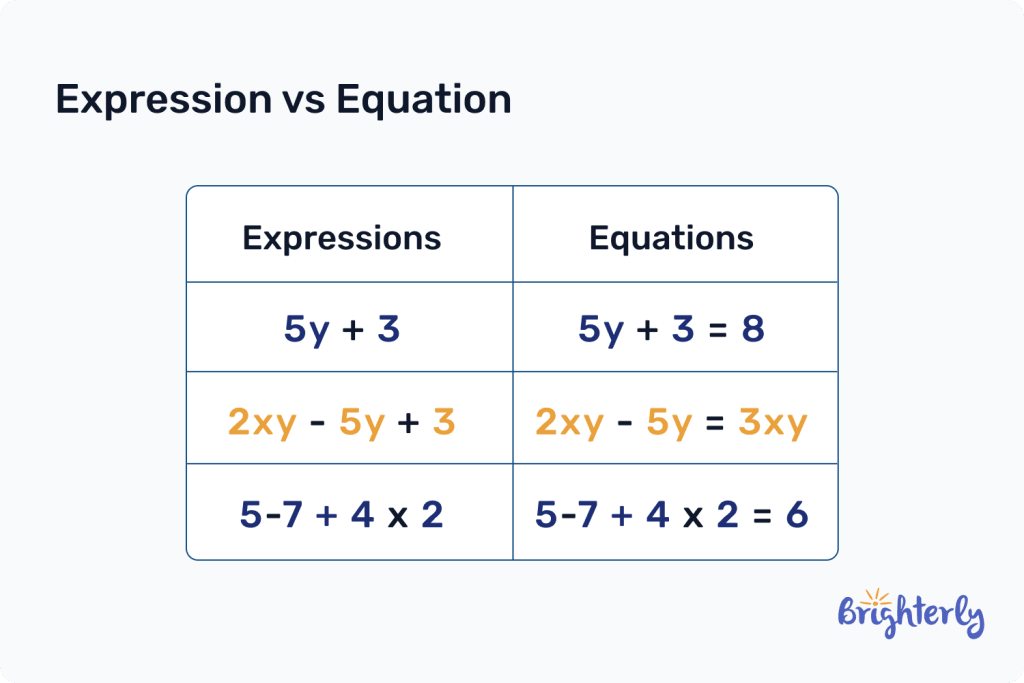
Expression vs equation

Expressions and equations are two related, but different, math concepts. Here are the differences in equation vs expression.

An equation is a mathematical statement that shows two expressions that are equal to one another. It can be considered an expression with a complete answer. For example, 3x + 2 = 8 is an equation because it shows that the expression 3x + 2 is equal to the number 8.

Expressions don’t need to have the equal portion, or in other words, the answer. They represent mathematical relationships, but they don’t show how these relationships can be used to solve the unknown quantities.

In an equation, you’ll be able to find the value of your variable, and that is often the goal of an equation. That’s the difference between expression vs equation in math.

How to write an expression in math

To write an expression, you’ll need to organize your constants, variables, operators and terms into a logical format.

If you are given a mathematical statement, for example, add 3 to 6, your expression will be 3 + 6.

Solved math tasks: examples

Now that you’ve learned the essential information on expressions, we’ve put together some solved math tasks to help you practice your knowledge. See if you can answer these questions and check your answers at the end!

Solved math task 1:

Simplify the expression (3x – 7) + 2(5x + 4).

Answer:

First, apply the distributive property to the second part of the expression: (3x – 7) + (10x + 8).

Next, remove the parentheses: 3x – 7 + 10x + 8.

Combine the like terms 3x and 10x to get 13x, and the like terms -7 and 8 to get 1. The simplified expression is 13x + 1.

Solved math task 2:

Simplify the expression 4(2x – 3) – (x + 5).

Answer:

First, use the distributive property to multiply 4 by both 2x and -3: 8x – 12 – (x + 5).

Next, distribute the negative sign to both x and 5: 8x – 12 – x – 5.

Finally, combine the like terms 8x and -x to get 7x, and the like terms -12 and -5 to get -17. The simplified expression is 7x – 17.

Solved math task 3:

Simplify the expression 5(3x + 6) – 2(4x – 3).

Answer:

First, apply the distributive property to both parts of the expression: (15x + 30) – (8x – 6).

Next, distribute the negative sign to both 8x and -6: 15x + 30 – 8x + 6.

Combine the like terms 15x and -8x to get 7x, and the like terms 30 and 6 to get 36. The simplified expression is 7x + 36.

Expression in math: practice math problems

Expression in math: worksheets

We have a range of free math worksheets that will help you to learn and practice your knowledge on expressions. Check our our cool worksheets: 

• Evaluating expressions worksheets
• Multiplying and dividing rational expressions worksheets
• Equations and inequalities worksheets
• Order of operations with integers worksheets

Camille Ira B. Mendoza

21 articles

I am a seasoned math tutor with over seven years of experience in the field. Holding a Master’s Degree in Education, I take great joy in nurturing young math enthusiasts, regardless of their age, grade, and skill level. Beyond teaching, I am passionate about spending time with my family, reading, and watching movies. My background also includes knowledge in child psychology, which aids in delivering personalized and effective teaching strategies.