• Math tutors
• /
• Knowledge Base
• /
• Linear Graph – Definition with Examples

Linear Graph – Definition with Examples

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on October 8, 2024

Brighterly math tutors, we simplify math concepts and make them easy and fun to learn.

Here, we’ll cover linear graphs, taking you through what a linear graph is, the equation, examples of linear graphs and how to plot a linear graph, and we’ll share solved math problems to help you practice your learning.

What is a linear graph?

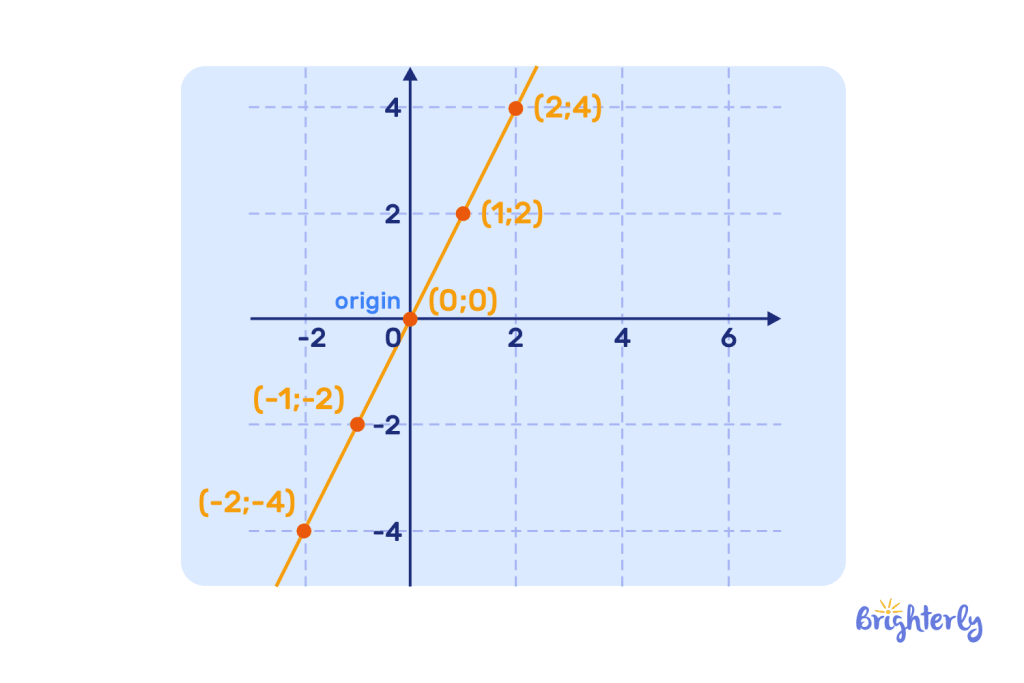
A linear graph represents a linear equation with two variables (x and y) in the form of a graph. It’s formed of a straight line on a two-dimensional graph or coordinate system. This line never bends or curves.

Here’s an example of linear graphs:

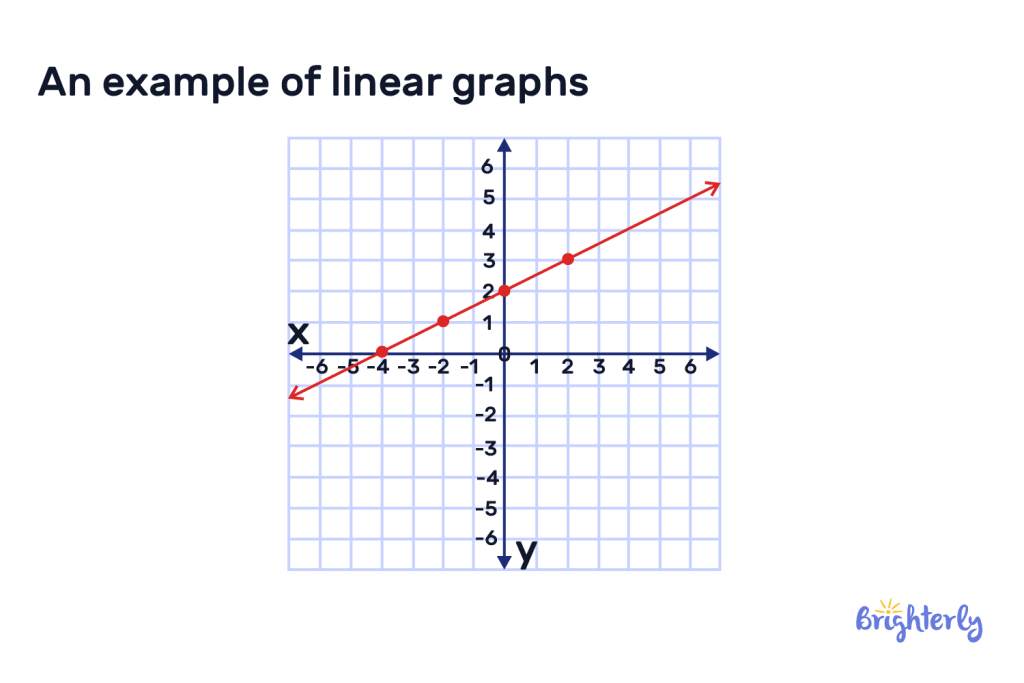
Linear graph definition

A linear graph is a straight line that connects two variables on a graph created from a linear equation. A linear graph will always be straight and never deviate from its straight slope.

The definition of linear in math comes from the word ‘line’, which is an easy way to remember that different linear graphs have straight lines.

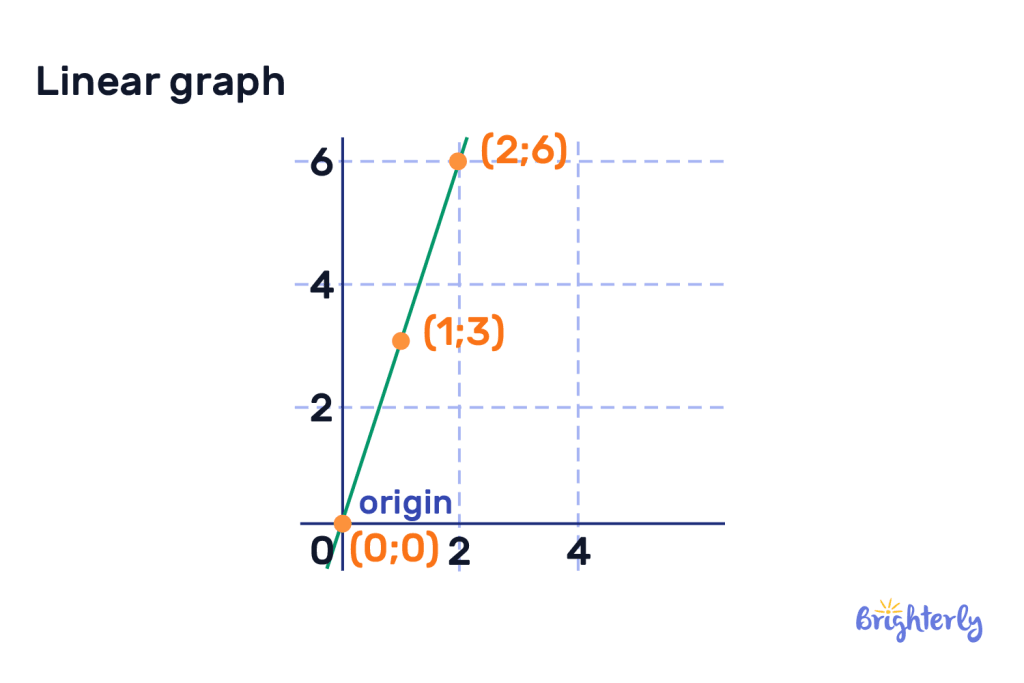
Different linear graphs have real-world applications, including calculating your savings, representing the acceleration of a car and even predicting future populations. This means they go beyond the world of math and are key in other disciplines, including economics, physics and engineering.

What does a linear graph look like?

A linear graph will have an x-axis (horizontal) and a y-axis (vertical). It will feature a straight, unbent line that represents the relationship between the x coordinate and the y coordinate.

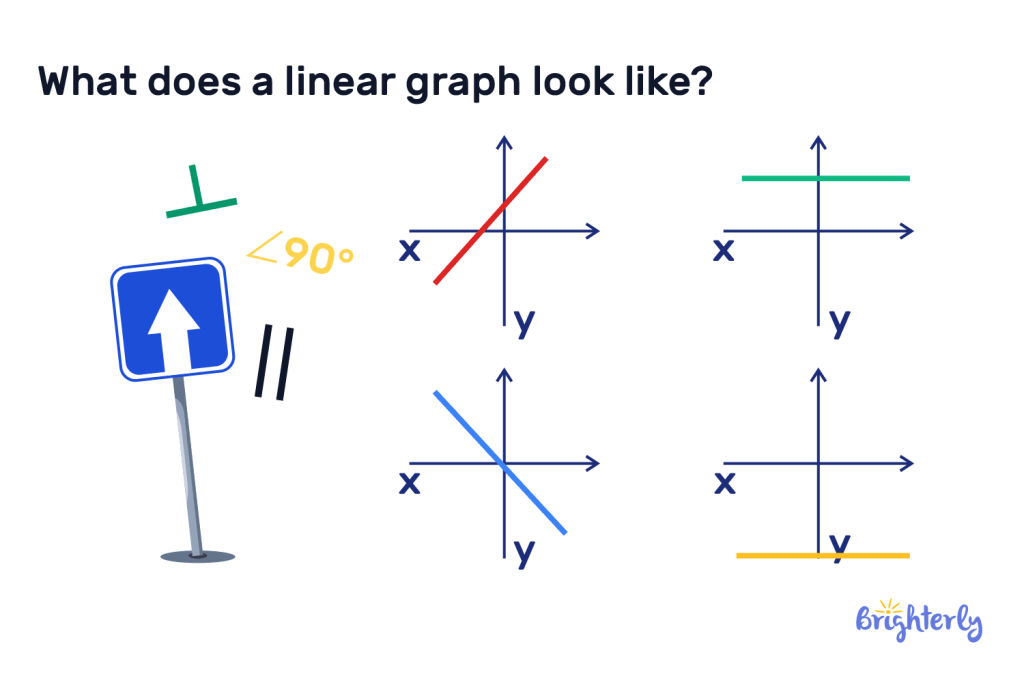
What is a straight line on a graph called?

A straight line on a graph is called a linear graph.

Math tutors

Join Brighterly for personalized lessons for your child

Meet the best tutors for interactive math learning.

Book free lesson

Linear graph vs line graph: difference

There are differences between linear graphs and line graphs. Both use lines to represent relationships between variables, but they’re not always the same thing.

Types of graphs: linear

A linear graph will always feature a straight line on a graph that represents a linear equation. It’s straight because it represents a consistent relationship between the two variables. This means that with every unit change in the x-axis (the input), the y-axis (output) changes by a consistent amount, resulting in a straight slope.

Types of graphs: line

A line graph, however, is a broader type of graph. These graphs also represent data and often equations, that change over time, but the relationships don’t need to be linear – i.e. consistent. The lines on a line graph can be curved, bent or zig-zagged to show changing variables.

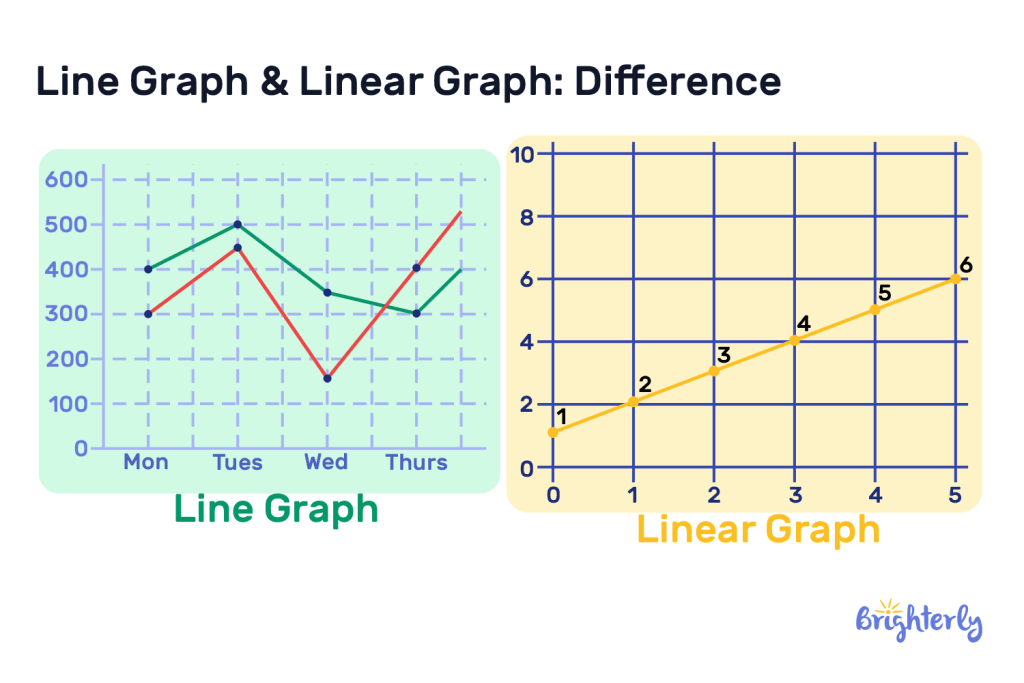
An easy way to remember the difference is to understand that different linear graphs are line graphs, but not all line graphs are linear graphs.

What is a linear graph equation?

The linear graph equation is: y = mx + c.

The elements represent the following:

• ‘y’ represents the output (dependent variable)
• ‘m’ represents the slope of the line and the rate at which y changes for a unit change in x
• ‘x’ represents the input (independent variable)
• ‘c’ represents the y-intercept

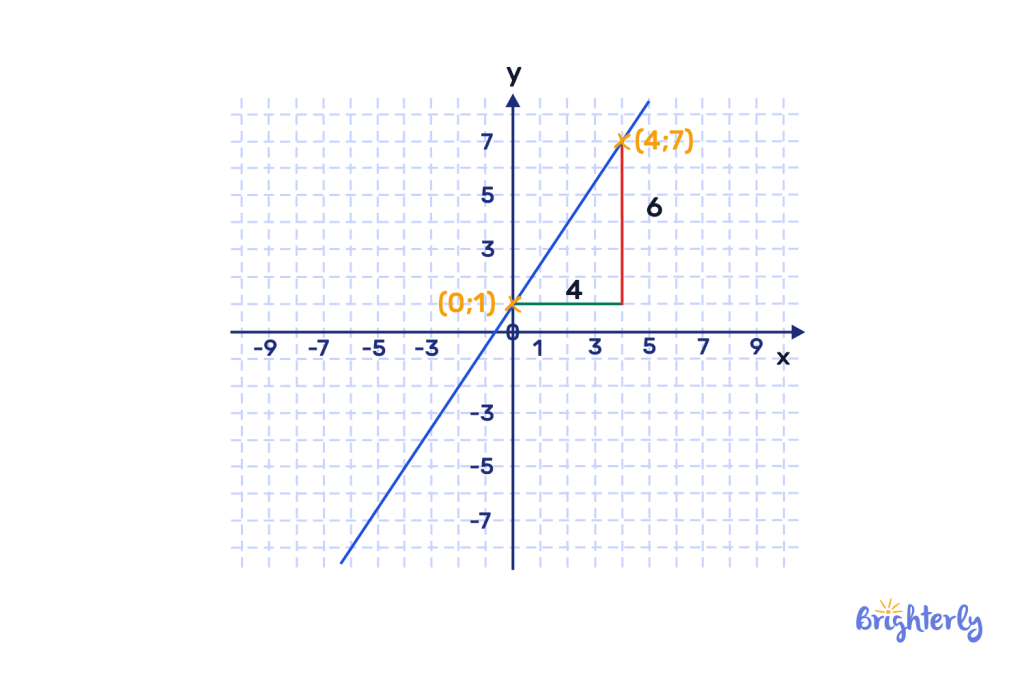
How to plot a linear graph

You can easily plot a linear equation on a graph with these simple steps:

1. Use the equation y = mx + c to identify the slope (m).
2. On the y-axis, mark the y-intercept (c).
3. Plot your additional points by moving from the y-intercept along the slope, moving upwards if the trend is positive and downwards if it’s negative.
4. Finally, connect all your points with a straight line.

Solved math tasks: examples

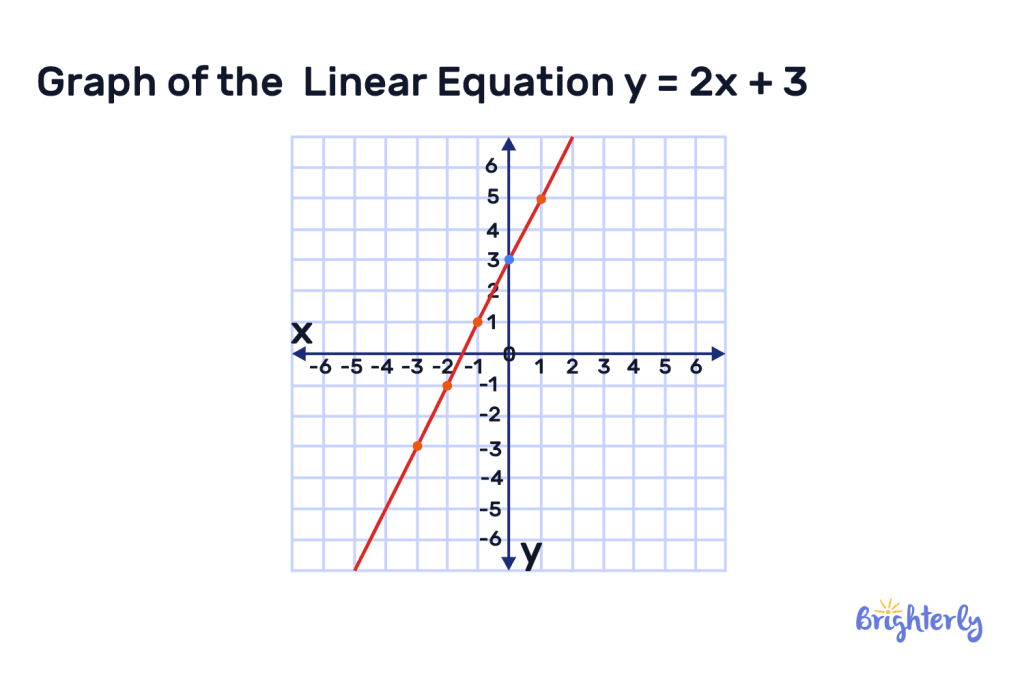
Solved math task 1

You have an equation of y = 2x + 3, where the y-intercept is 3 and the slope is 2. 

Plot out this linear graph, starting from point (0,3) on the y-axis and moving two units up for every increase on the x-axis. Then, connect your points to form your linear graph.

Answer:

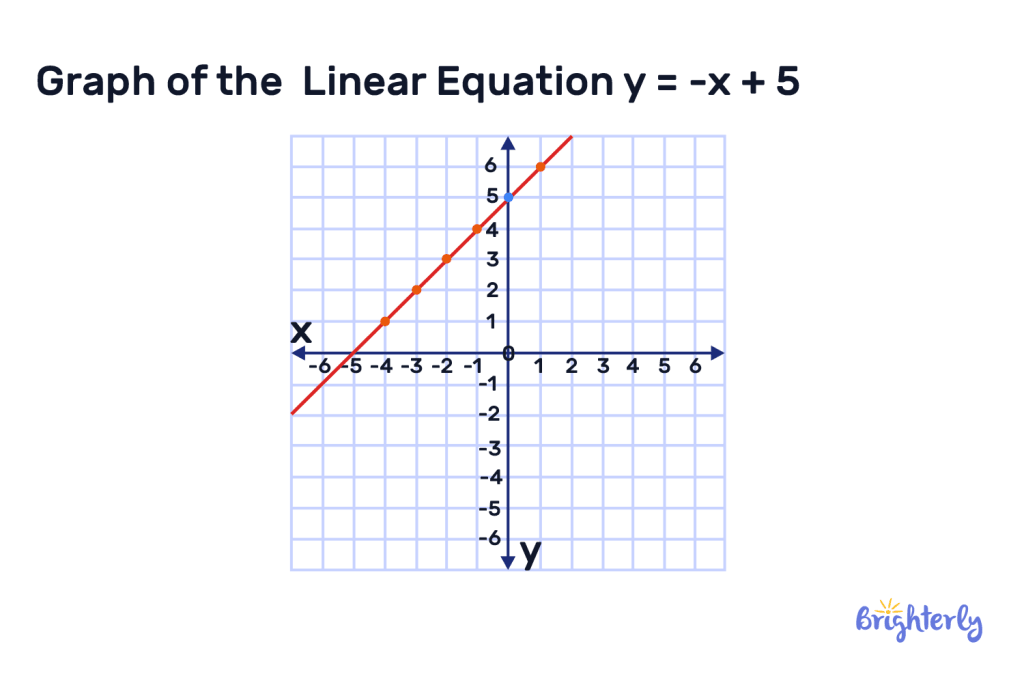
Solved math task 2

You have an equation of y = -1x + 5, where the y-intercept is 5 and the slope is -1. 

Plot out this linear graph, starting from point (0,5) on the y-axis and moving one unit down for every decrease on the x-axis. Then, connect your points to form your linear graph.

Answer:

Linear graph: practice math problems

Linear graph worksheets

We’ve created a number of math worksheets on different linear graphs and key-related math concepts to help you fully understand and practice this math concept:

• Slope worksheets
• Kindergarten graphing worksheets
• Graph worksheets
• Line graph worksheets

Jessica Kaminski

72 articles

Jessica is a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.