• Math tutors
• /
• Knowledge Base
• /
• Order Of Operations – Definition, Steps, Examples

Order Of Operations – Definition, Steps, Examples

Camille Ira B. Mendoza

reviewed by Jo-ann Caballes

Updated on October 28, 2024

The order of operations is the sequential process we follow to solve math problems. This article contains the order of operations in math, explains why we follow this order, and teaches you how to do so too through our order of operations definition and order of operations examples

What is the order of operations?

The order of operations is a set of mathematical rules that guide the way we approach any calculation. 

Order of math operations examples

If we were to calculate this equation: 12 + 10 × 8 – 9.

The answer we get will be different if we solve it in order from left to right or from right to left. 

If we solved it from left to right, we would first add 12 + 10 to give 22, then multiply by 8 which gives 176, and minus 9 which equals 167.

If we solved from right to left, we would subtract 8 from 9 to give 1, then multiply by 10 which gives 10, and add it with 12 to give 22.

Both of these answers are inaccurate, yet, the only way to get the correct answer will be to follow the order of operations. 

The math operations order dictates that multiplication comes before addition or subtraction which means we need to first multiply 10 by 8 which is 80, then sum it with 12 to give 92, and minus it by 9 for the correct answer which is 83.

This is the same for other equations such as: 

• 6 + 4 × 7 – 9 
• 3 + 2 × (5 – 2) ÷ 2
• 7– 2 × (4+1)

The order of operations has to be followed to appropriately solve these equations.

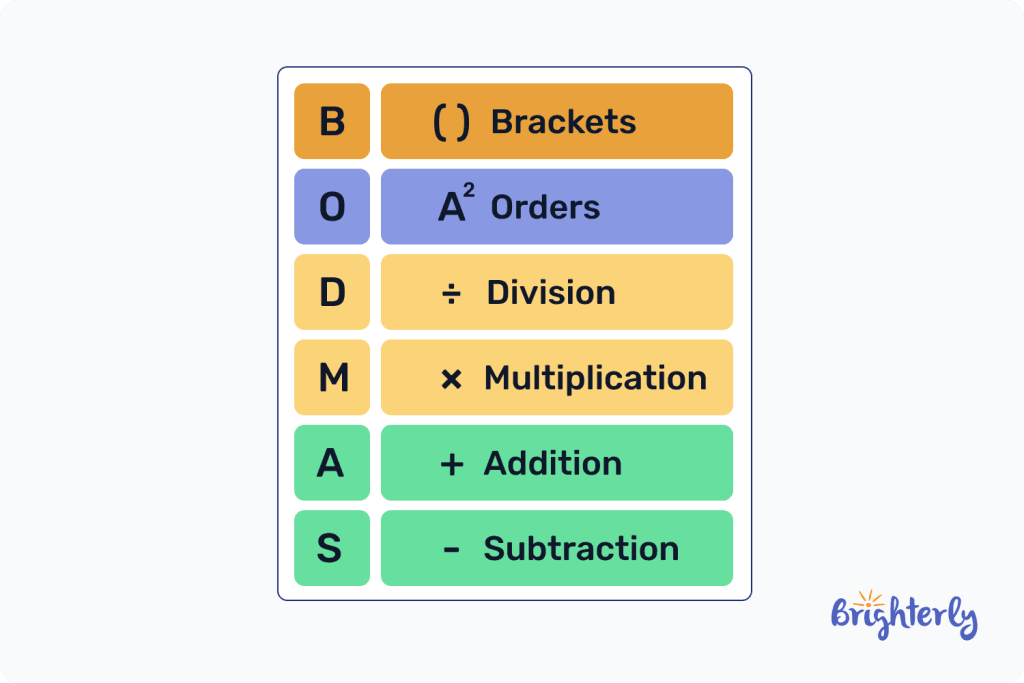
Order of Operations Steps:

The order of operations is in a sequence of steps that cannot be skipped regardless of where each arithmetic operation occurs in the equation. 

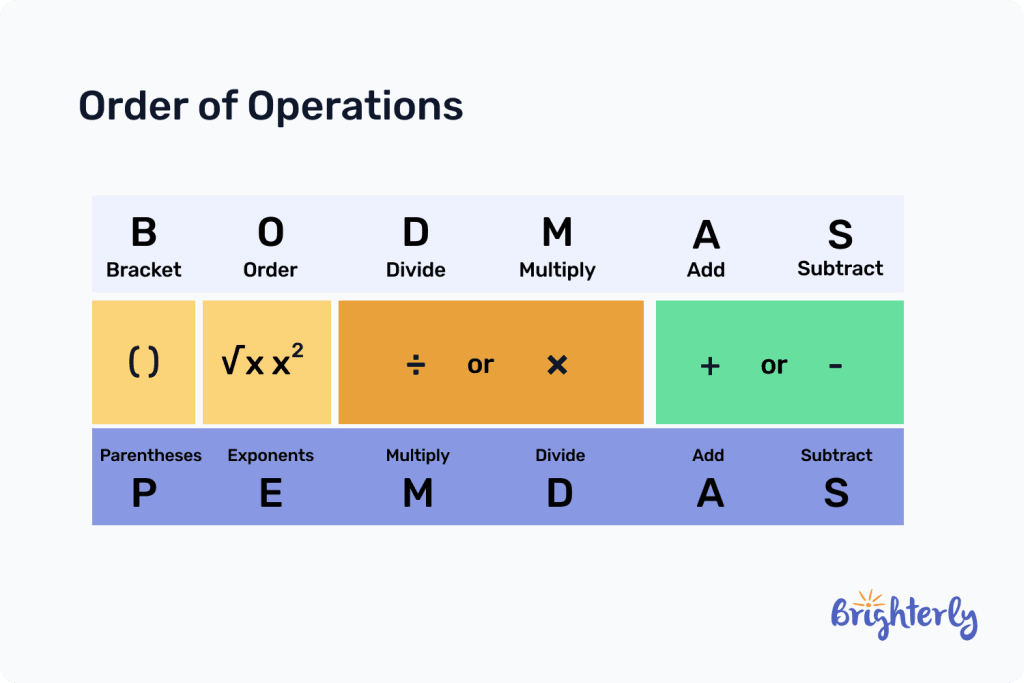
The steps of the order of operations can be memorized with the acronym; PEMDAS. 

Parentheses, exponents multiplication/division, addition/subtraction

Parentheses: 

Also known as brackets, the parentheses are used to group numbers and expressions together.  Calculating the parentheses is the first step in the PEMDAS order of operation. The parentheses are identifiable by their symbol ( ). 

Exponents:

The exponents are used to express when a number is multiplied by itself. It is second in the order of PEMDAS. Exponents can be represented with x2 

Multiplication or Division:

The next in line is multiplication or division, depending on which of these arithmetic operations comes first when we solve from left to right. Their symbols are × for multiplication and ÷ for division.

Addition or Subtraction

The last in the order of operations is addition and subtraction. We solve for it in the equation depending on which of these two comes first when we solve from left to right. The symbol for addition is + and subtraction is –

PEMDAS examples

Parentheses example:  In an equation where the parentheses are used such as; 4(5), we solve it by multiplying the elements inside the brackets with the element on the left. Therefore 4 × 5 = 20.

Exponents example: If we had 53, this means 5 is multiplied by itself 3 times which is 5 × 5 × 5 = 125.

Multiplication or Division example: For multiplication; 3 × 4 is 12 and for division; 4 ÷ 2 is 2.

Addition or Subtraction example: If we were to add two numbers, 3 and 2, that would be 3 + 2 = 5, and if we were to subtract them, that would be 3 – 2 = 1.

Order of operations rules

To properly understand the concept, let’s go over the guiding operation rules:

Rule 1: We always begin with the parentheses ( ). We solve the numbers or expressions that are grouped within it to the outside. Note that even within the parentheses, the order of operations still maintains its sequence from left to right.

Rule 2: The next in line after the parentheses is exponents, we are to multiply whichever number holds an exponent by itself as much as the number it carries.

Rule 3: Multiplications and divisions should be done next from the left to the right.

Rule 4: In the order of operations, addition and subtraction is done from the leftmost part is the final step before we get our final answer. 

Note that in math, PEMDAS may also be known as BODMAS which stands for Bracket Orders Division Multiplication Addition and Subtraction. These two math operation orders are the same and are used to give accurate answers to math equations.

Solved Math Tasks “Order of operations” with answers

Solved math problem 1

Using the PEMDAS order of operations, what’s the answer to 5 – 18 ÷ 6 × 9 + 9?

Answer

Remember that we solve for whichever arithmetic operation comes first between multiplication and division and in this example, division comes first. This means we first divide 18 by 6; 18 ÷ 6 = 3. 

This makes the equation change to 5 – 3 × 9 + 9

Next in the arrangement is multiplication: 3 × 9 = 27

 5 – 27 + 9

Then subtraction:  5 – 27 = –22

–22 + 9 = –13

Solved math problem 2

With PEMDAS, how do we solve this equation: 132 ÷ (8 + 9 × 4) – 3. 

Answer

Remember that we always solve the parentheses first, and even within it, the order of operations must be followed. Therefore, we must first do the multiplication: 9 × 4 = 36

This changes the equation to 132 ÷ (8 +36) – 3

We still aren’t done with the parentheses so we do the addition within it: 8 +36 = 44

132 ÷ 44 – 3

Next is the division: 132 ÷ 44 = 3

3 – 3 = 0

Solved math problem 3

Using the order of operations, solve the equation  5 + 7 × (4 + 2) ÷ 2 – 4.

Answer

We start with the parentheses, (4 +2) = 6.

So, our equation changes to 5 + 7 × 6 ÷ 2 – 4

Then, we multiply 7 by 6 which equals 42

5 + 42 ÷ 2 – 4

Next is division: 42 ÷ 2 = 21

5 + 21 – 4

The addition; 5 +21 = 26

And lastly subtraction: 26 – 4 = 22.

Order Of Operations: Practice Math Problems

Order Of Operations: worksheets

Now that we’ve gone over how to properly approach any math problem by explaining the order of operations meaning, and giving a relevant order of operations example, young learners can practice more on their own using Brighterly’s free worksheets:

• Order of operations worksheets
• PEMDAS worksheets 
• Order of operations worksheets for 5th graders
• 6th-grade order of operations worksheet 

Camille Ira B. Mendoza

21 articles

I am a seasoned math tutor with over seven years of experience in the field. Holding a Master’s Degree in Education, I take great joy in nurturing young math enthusiasts, regardless of their age, grade, and skill level. Beyond teaching, I am passionate about spending time with my family, reading, and watching movies. My background also includes knowledge in child psychology, which aids in delivering personalized and effective teaching strategies.