How to Calculate Percent Difference – Definition, Formula, Examples
reviewed by Jo-ann Caballes
Updated on November 12, 2024
Percent difference is used to find the relative variation between two values through the absolute difference, the average of values, and percentage.
Here, we would learn about the percent difference calculation, give relevant examples, practice questions and more to help young learners understand this topic.
What is the percent difference?
The percent difference is a method that shows the relationship between two values through the use of absolute difference. The result of the percentage difference equation is expressed in percentages.
The absolute difference is found by subtracting one value from another, regardless of whether the result is positive or negative.
For instance, the absolute difference between 15 and 20 is expressed as |15 — 20| = 5.
The answer is not negative because the absolute difference is just finding the magnitude of the difference between the two values.
You may wonder “Why do we learn it and what does percent difference tell you?”. Well, it helps in analyzing data and understanding the relationship between two values. However, it does not tell us the decline or increase in the values — this is done through percentage change. We discuss the differences between the two later in the article.
Percent difference formula
The percentage difference formula is calculated by finding the absolute difference between the two values, then dividing that difference by the average of both values and multiplying it by 100.
We find the average of both values by adding them and dividing by 2.
The difference formula can thus be expressed as:
|absolute difference between two values| / average of both values × 100%
When the values are represented as a and b, the formula is:
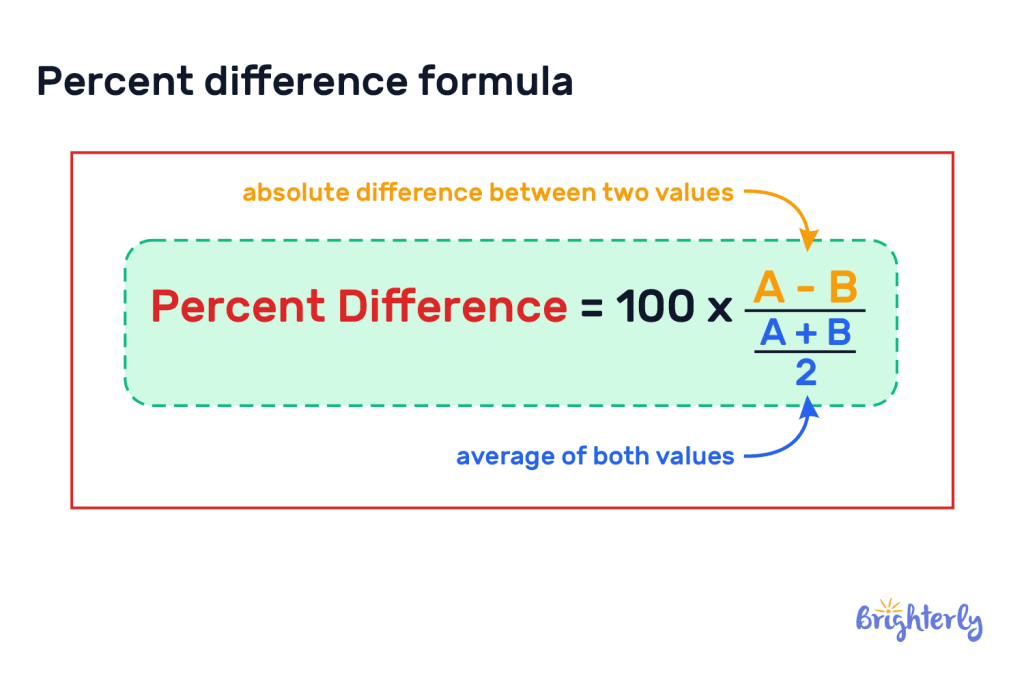
Calculating percent difference
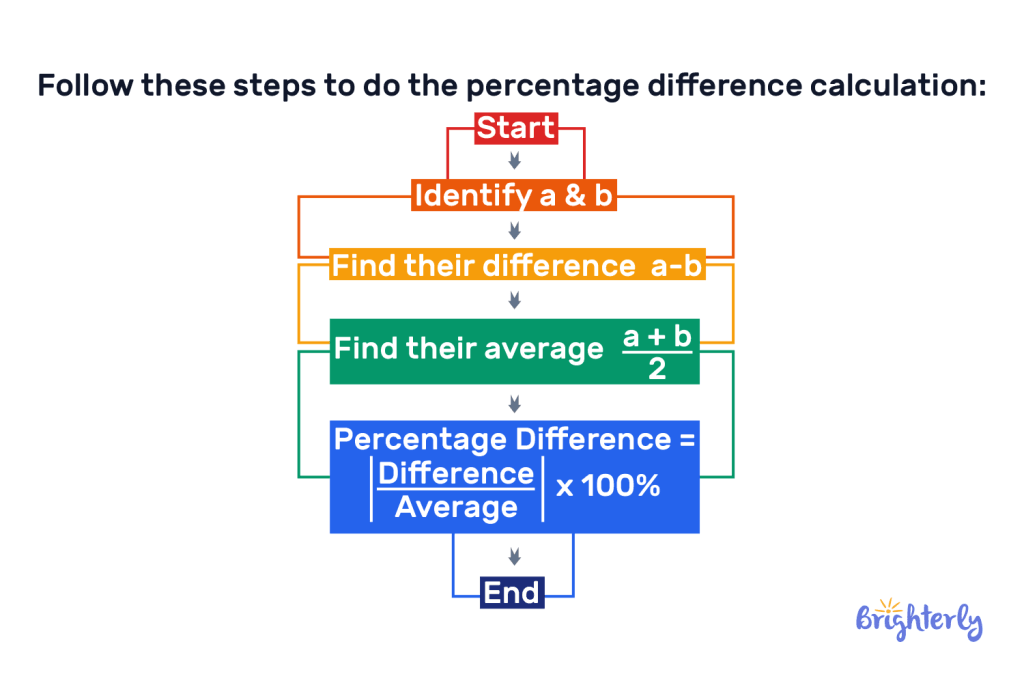
Follow these steps to do the percentage difference calculation:
STEP 1
Find the absolute difference between the two values given. If we are given 5 and 8 as our values. We solve for the absolute difference as so: |8 — 5| = 3. The absolute difference is 3.
STEP 2
We find the average of the values by adding them and dividing the result by 2. Let’s use 8 and 5 again. The average would be 8 + 5 = 13 / 2 = 6.5.
STEP 3
Finally, to arrive at the percentage difference, we would divide the absolute difference (3) by the average (6.5), then multiply by 100.
The relative percent difference for 8 and 5 is 46.15%.
Note that your answer should always have the percentage symbol (%) because the answer is in percentage.
Percent difference vs Percent Change
Percentage difference and percentage change are two separate concepts. We know what the percentage difference is, but what is the percentage change?
Here are their differences:
| Percentage Difference | Percentage Change |
| The equation for Percent Difference is |absolute difference| / average × 100 | The formula for Percentage Change is (Final value — Initial value) / initial value × 100 |
| The result just tells us the percentage difference between the two values without specifying which is larger. | The result tells us the amount of change from a previous value to the most recent value |
| The percentage difference is always positive | The percentage change is either positive when there is an increase in change of values or negative when there is a decrease. |
| The denominator is the average of the values | The denominator is the initial value |
| This is mostly used to show the relationship between values | This is used to show the overtime transition from one value to another |
Solved Math Tasks: Examples
Solved math problem 1
Using the steps for calculating the percentage difference above, what is the percentage difference between two values when a = 17 and b = 59?
Answer
|17 — 59| / 17 + 59/ 2 × 100
First, the absolute difference: |17 — 59| = 42
Then, the average of the values: is 17 + 59 = 76 / 2 = 38.
Thirdly, we divide both and then multiply by 100; 42 / 38 × 100 = 110%.
|
The percentage difference between values 17 and 59 is 110%. |
Solved math problem 2
Answer the following questions with Yes/ No answers:
- Can the percent difference be negative?
- Is percentage change different from percentage difference?
- Can we find an increase or decrease in the percentage difference?
Answer
|
Solved math problem 3
Molly sells 53 chocolate bars for her school fundraiser and Joan sells 37, what is the percentage difference?
Answer
Again, we first find the absolute difference:
|53 — 37| = 16
Then the average: 53 + 37 = 90/ 2 = 45
16 / 45 × 100 = 35%
|
Therefore, the percentage difference between Molly’s and Joan’s sales is 35% |
Solved math problem 4
In a class, a student has a cumulative grade point average of 4.7 and another student has 3.0. Find the percentage difference between their two results.
Answer
|4.7 — 3.0| = 1.7
4.7 + 3.0 = 7.7/ 2 = 3.85
1.7 / 3.85 × 100 = 44%
|
The percentage difference between both results is 44%. |
Solved math problem 5
The Washington Monument is 555 feet tall and the Statue of Liberty is 305 ft. What is the percentage difference between these two monuments?
Answer
|555 — 305| = 250
555 + 305 = 860 / 2 = 430
250 / 430 × 100 = 58%
|
The percentage difference between the two monuments is 58%. |
How to Calculate Percent Difference: Practice Math Problems
How to Calculate Percent Difference: worksheets
Understanding the percent difference equation helps young students explore comparative statistics and relative measurement.
Learn more about percentages and measurements through our free worksheets:
Math homework help for grade 1-8
Get the homework support your child needs!
Choose kid's grade
Math Program
Boost Your Child's Math Abilities! Ideal for 1st-8th Graders, Perfectly Synced with School Curriculum!
