• Math tutors
• /
• Knowledge Base
• /
• Perfect Numbers: Definition, Examples, and Solved Math Tasks

Perfect Numbers: Definition, Examples, and Solved Math Tasks

Camille Ira B. Mendoza

reviewed by Jo-ann Caballes

Updated on October 28, 2024

Here comes another portion of helpful material from Brighterly, where you’ll learn the theoretical basis of a specific math concept and practice applying it during exercises.

In this guide, we’re talking about perfect numbers. What are they? Why are they called “perfect”? And what’s the theorem underpinning them? All these concepts, along with the hands-on tasks and worksheets, are covered in this guide.

What Is a Perfect Number?

A perfect number is a positive integer, which equals the sum of its factors, excluding the number itself.

Perfect Number Definition

A perfect number is an integer expressed as the sum of its proper factors. These should be the factors excluding the number itself.

The smallest perfect number is 6. The other examples include 28, 496, and 8128. Let’s explain what the perfect number is in the example of 6. 

• The number has proper divisors 1, 2, and 3.
• The sum of 1 + 2 + 3 makes 6.

Here comes another example of 28:

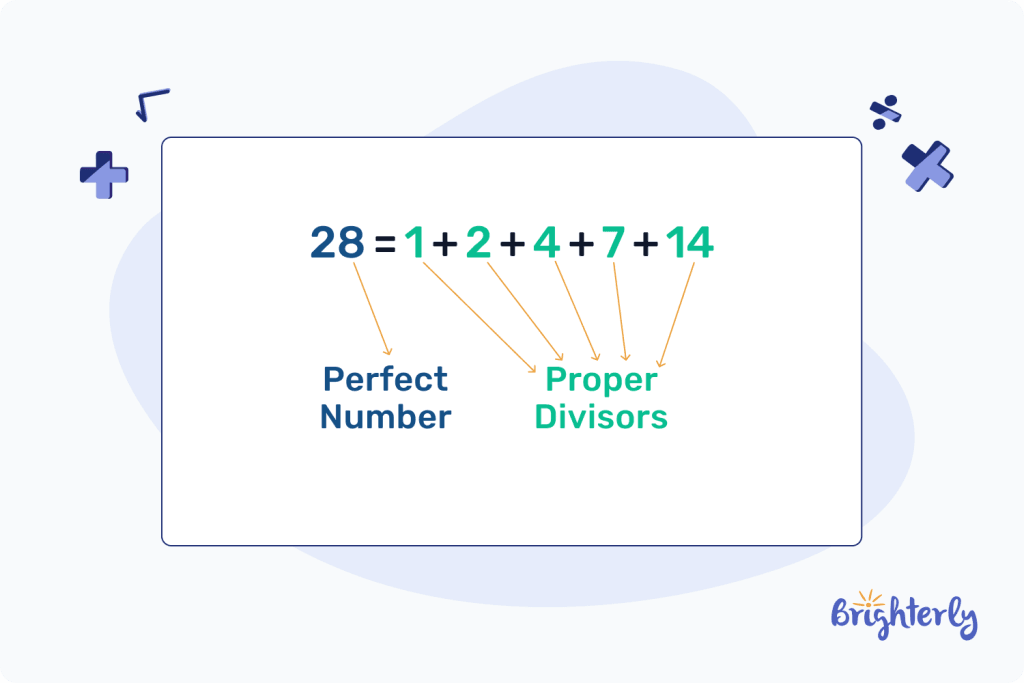
Even Perfect Numbers: Theorem

The even number theorem states that all perfect numbers can be expressed as N = 2n-1(2n – 1). In the equation 2n – 1 is a prime number.

Let’s assume that n = 3 for an example. Then,

23-1(23 – 1) = 22(8 – 1) = 22*7, = 4*7 = 28

This way, we get a perfect number 28.

Perfect Numbers Chart

A perfect number chart shows the divisors of a number. If we add up all those, we will receive the perfect number itself. Here’s a closer look:

Perfect Numbers From 1 to 100

The perfect numbers from 1 to 100 are 6 and 28. 

But hey, a perfect numbers list is a short thing overall. Then, how many perfect numbers are there? You’ll be surprised, but only 51 have been discovered up to date. The latest one emerged in 2018. 

You are already acquainted with the first to fourth numbers. Now, here are some others, smaller to larger, just to show you how huge they may get:

1. 6
2. 28
3. 496
4. 8128
5. 33550336
6. 8589869056
7. 137438691328
8. 2305843008139952128
9. 2658455991569831744654692615953842176

By the way, to define a perfect number, one has to devote much work and skill. Just think about it: the last number discovered grows to stunning 49,724,095 digits.

Math tutors

Join Brighterly for personalized lessons for your child

Meet the best tutors for interactive math learning.

Book free lesson

Solved Math Tasks: Examples

Ok, by now, you must be well aware of what perfect numbers are. But practice is where the real fun begins. 

Try to solve these math tasks to see if you have perfected the topic.

Task 1

List the first four perfect numbers and the corresponding values of n that generate them using the formula N = 2n-1(2n – 1).

Solution:

Task 2

Using the formula, calculate the perfect number for n = 5.

Solution:

Task 3

Why is the number 496 called perfect? List its proper divisors and calculate their sum to prove the status of this number.

Solution:

We can call 496 a perfect number since it matches all the requirements.

Task 4

Use the formula to create a list of perfect numbers for n = 2, 3, 5, and 7.

Solution:

Using the formula  N = 2n-1(2n – 1):

• For n = 2:

• For n = 3:

• For n = 5:

• For n = 7:

Task 5

If we substitute n = 4 into the formula  N = 2n-1(2n – 1), will it give us a perfect number?

Solution:

First, we need to substitute 4 into our perfect number equation:

• 24- 1 = 16 – 1 = 15

But 15 is not a prime number. The reason — it can be factored into 3*5.

Perfect Numbers: Practice Math Problems

Perfect Numbers: Worksheets

Now that you know the perfect number meaning and actual numbers on the list, it’s time for extra practice. Looking for more tasks? We have prepared them for you!

Download any of these Brighterly worksheets and start practicing in a convenient format:

• Mixed Numbers Worksheets
• Math Worksheets 2 Digit Divisors
• Distributive Property Of Multiplication Worksheets

Camille Ira B. Mendoza

21 articles

I am a seasoned math tutor with over seven years of experience in the field. Holding a Master’s Degree in Education, I take great joy in nurturing young math enthusiasts, regardless of their age, grade, and skill level. Beyond teaching, I am passionate about spending time with my family, reading, and watching movies. My background also includes knowledge in child psychology, which aids in delivering personalized and effective teaching strategies.