Symmetry – Definition, Examples, Practice Problems, FAQs
reviewed by Jo-ann Caballes
Updated on October 1, 2024
At Brighterly, we make learning math concepts fun and engaging.
Symmetry is a mathematical principle that’s essential to how we understand shapes, structures, patterns and more.
Here, we cover symmetry in math and its types and share practice test questions.
What is symmetry in math?
Symmetry meaning in math is an object that has two matching halves. Symmetrical shapes look the same if they’re mirrored.
Symmetry: definition
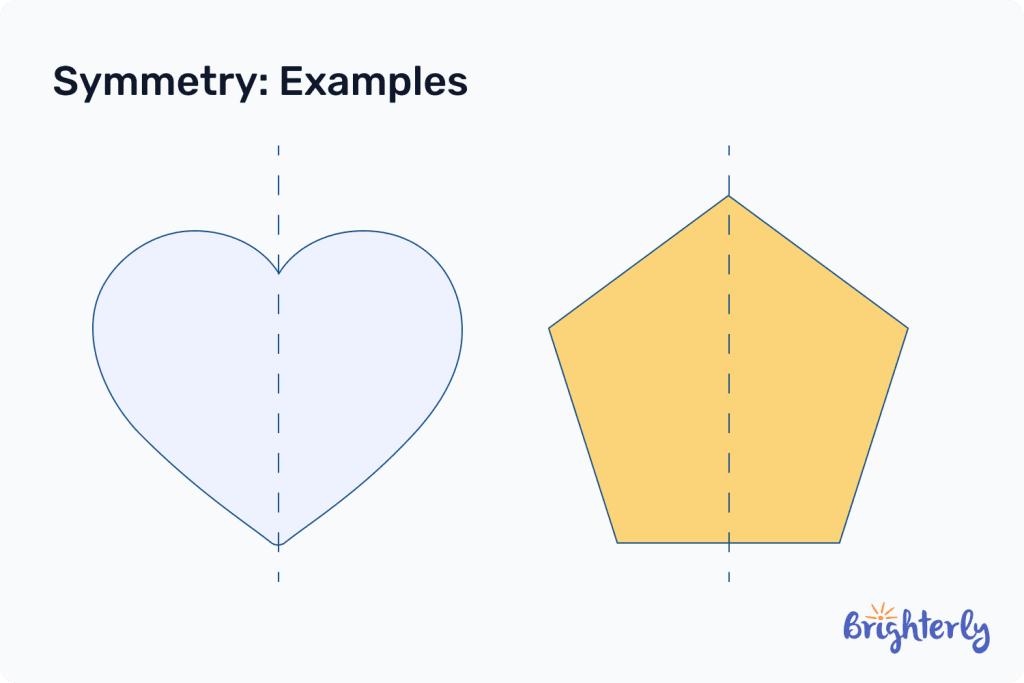
What does symmetry mean? The definition of symmetry is a shape with identical parts facing one another on an axis. There are different types of symmetry and lines of symmetry.
Here are some symmetry examples.
What is the line of symmetry?
The line of symmetry is an invisible axis line dividing the identical halves of symmetrical shapes. It’s also called a mirror line or reflection line.
Lines of symmetry in math operate like a mirror – the shape on each side is identical and looks reflected. Below we have some lines of symmetry examples.
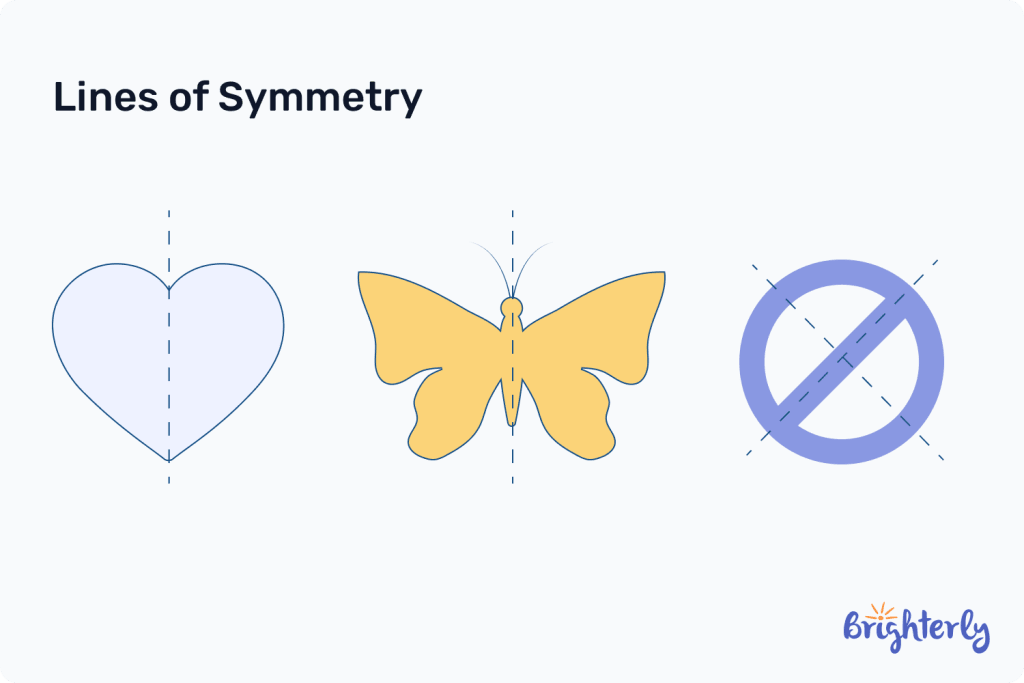
Types of lines of symmetry
There are three types of lines of symmetry:
- Vertical line of symmetry
- Horizontal line of symmetry
- Diagonal line of symmetry
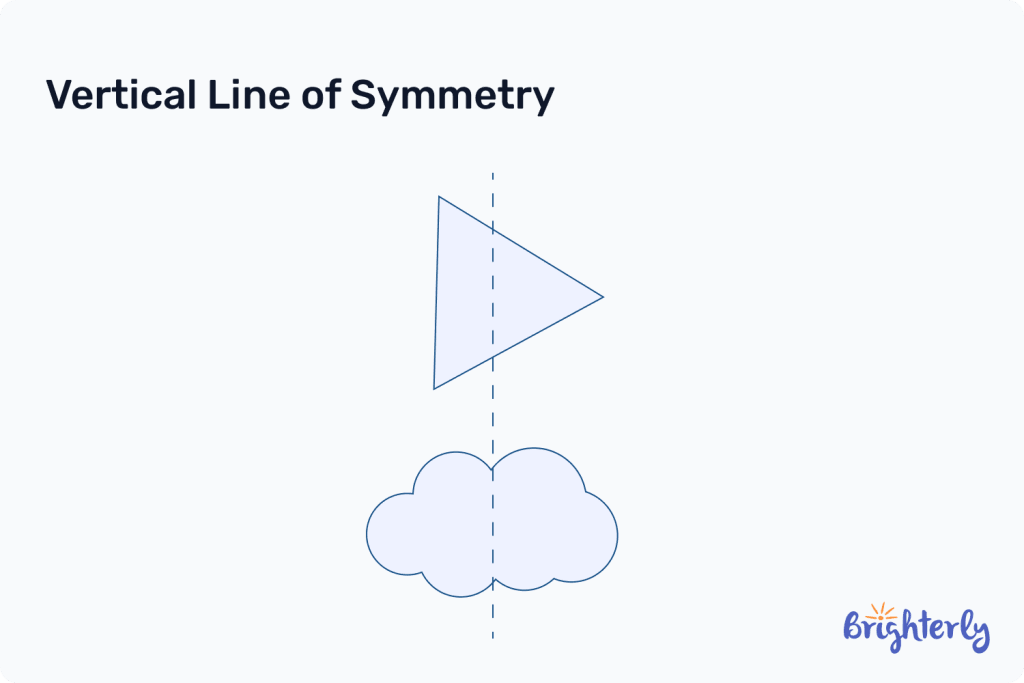
Vertical line of symmetry
A vertical line of symmetry runs up the y-axis from the bottom to the top of symmetrical shapes, splitting them into two congruent halves.
Many geometric shapes have vertical lines of symmetry, including squares and rectangles.
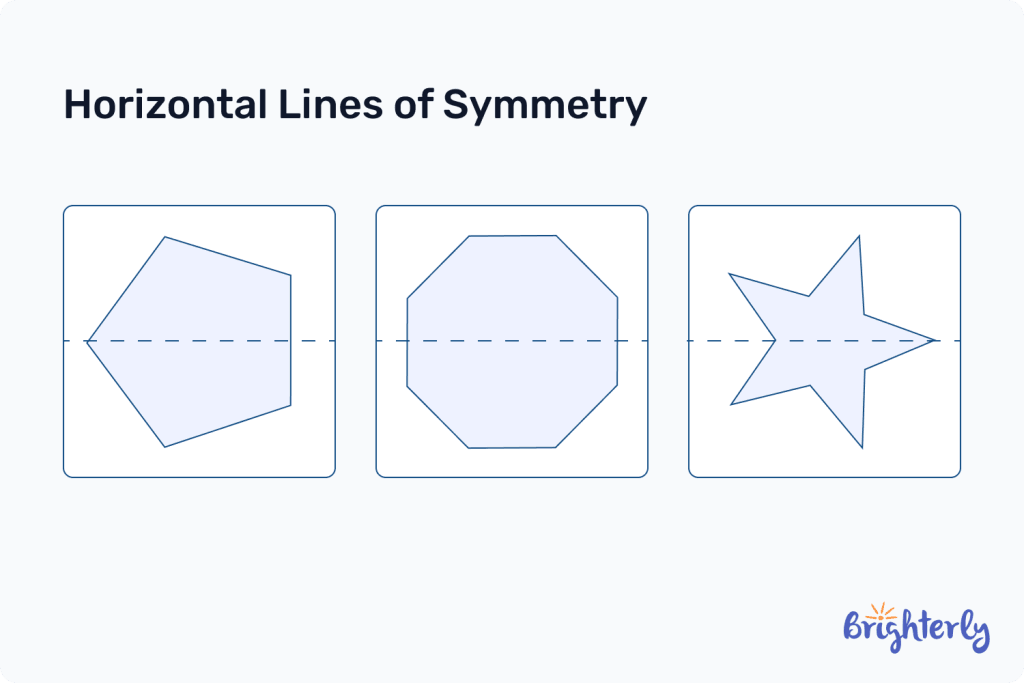
Horizontal line of symmetry
A horizontal line of symmetry runs across the x-axis of a symmetrical image from left to right. The image is mirrored above and below the line.
Again, many geometric shapes, including rectangles and squares, have horizontal lines of symmetry.
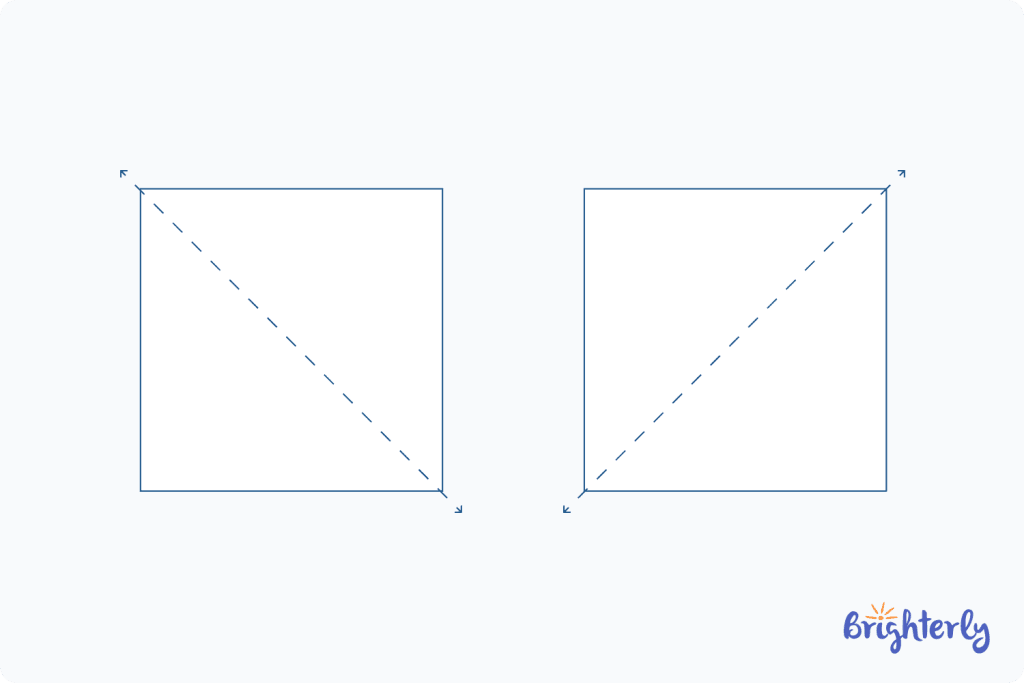
Diagonal line of symmetry
A diagonal line of symmetry runs diagonally from corner to corner. It also splits the image into two identical halves.
Symmetrical shapes such as circles, squares and rhombuses can be split with diagonal lines of symmetry.
Types of symmetry
There are different types of symmetry that cover more than just mirror images:
- Reflexive symmetry
- Translational symmetry
- Rotational symmetry
- Glide symmetry
- Point symmetry
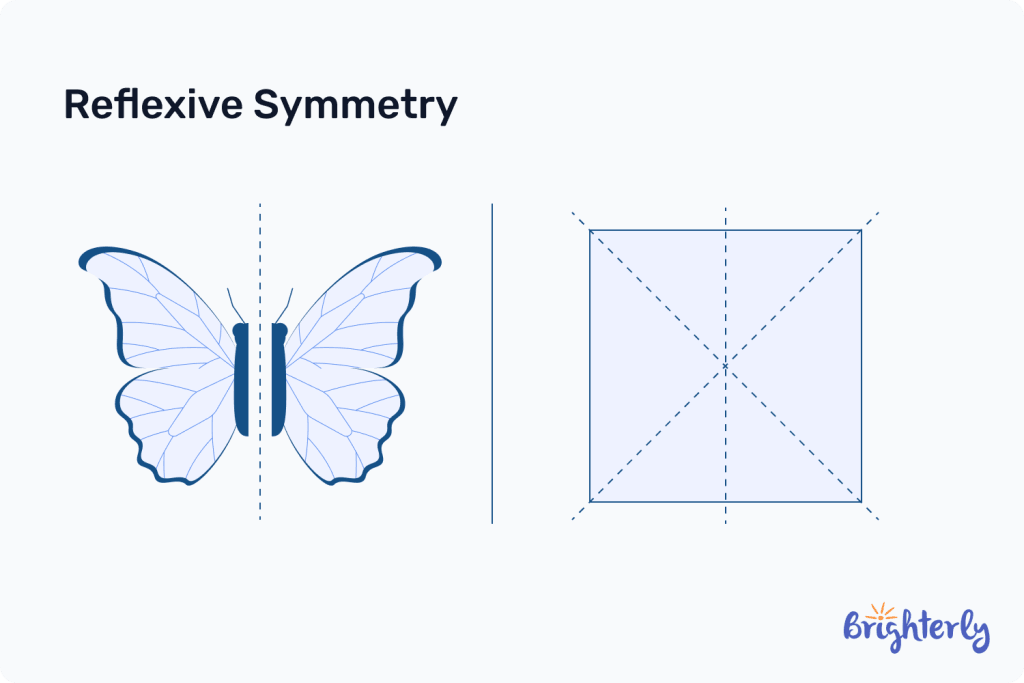
Reflexive symmetry
Reflexive symmetry is where a shape is reflected over a line of symmetry and is identical on both sides. This is the type of symmetry that’s most widely understood and can be seen in many shapes.
Translational symmetry
Translational symmetry is when an image or figure is moved (or translated) without being altered, reflected or rotated. If you superposed the images, they match perfectly.
Translational symmetry is key to understanding patterns, particularly tessellations – where identical shapes or figures fit together with no spaces in-between.
Rotational symmetry
Rotational symmetry requires a central point. You rotate an image by less than 360° and it still reflects the original image at a different angle. A snowflake has six-fold rotational symmetry – it’s rotated six times at 60° until the full snowflake is complete.
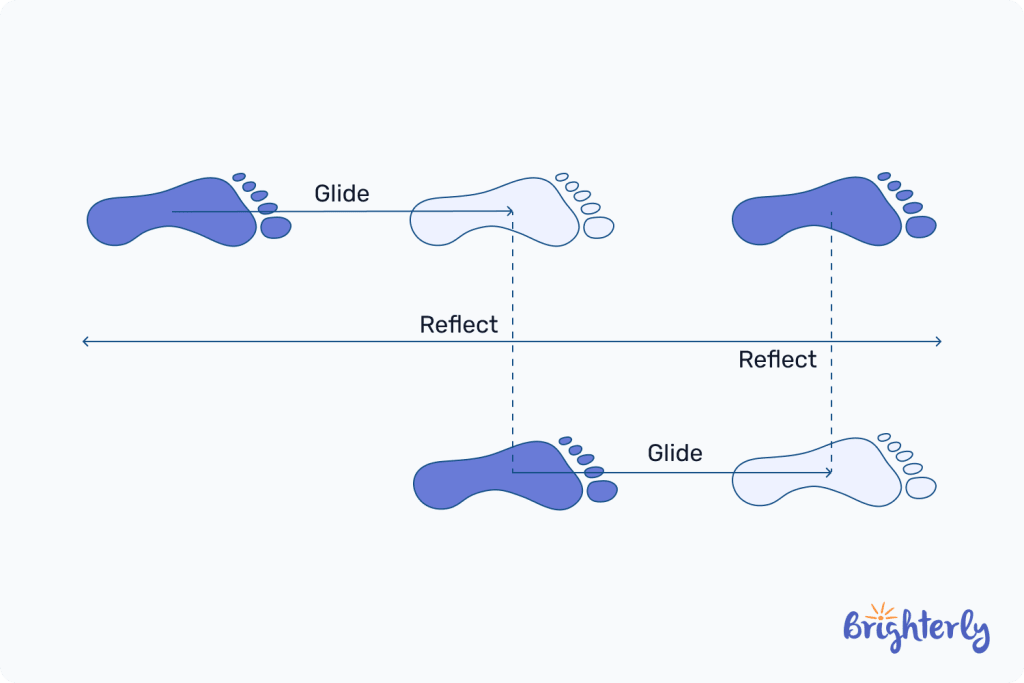
Glide symmetry
Glide symmetry (glide reflection) refers to an image that’s been glided along a line (i.e. reflected and translated) and remains identical to the original. For example, human footprints walking in a straight line.
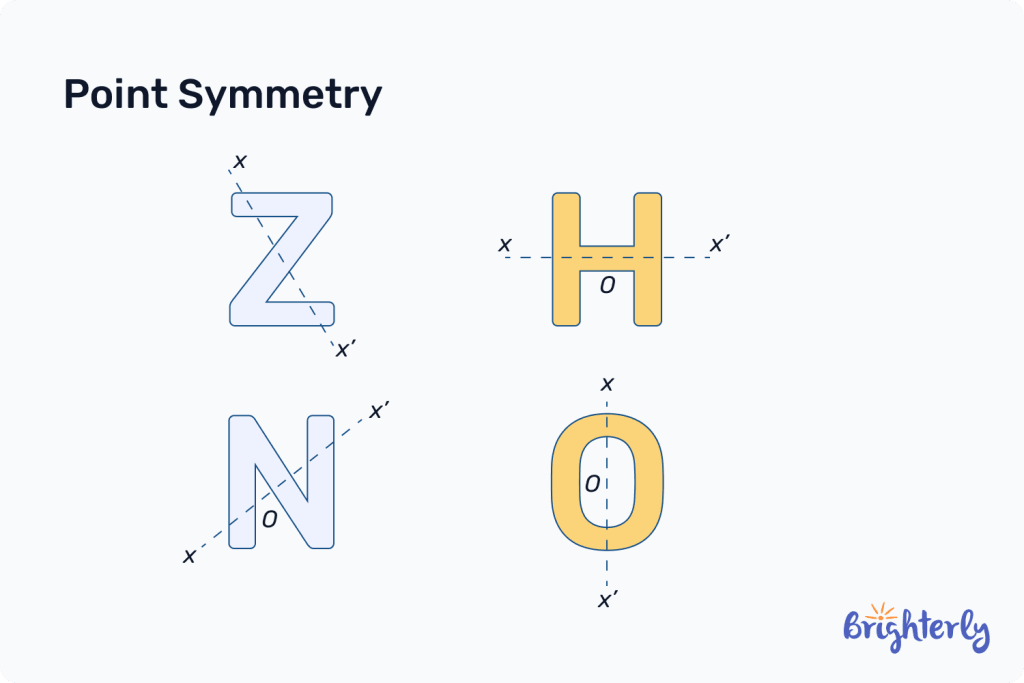
What is point symmetry?
Point symmetry is a shape identical to its original when rotated 180°. To visualize this, draw a graph with 4 equal quadrants and rotate your image from one quadrant to another.
The center of the graph will be the central point from which you rotate your image.
Solved math tasks: examples
Here are some examples of solved math tasks to practice your symmetry in math knowledge.
Use the figure to answer the questions:
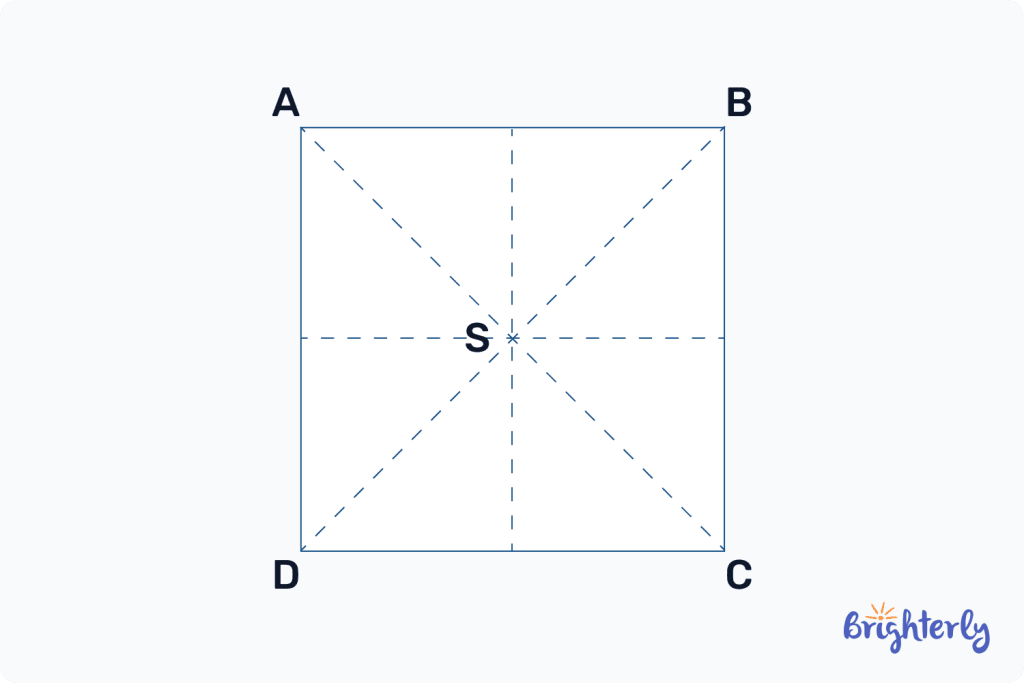
Solved math task 1
Draw all lines of symmetry in the figure and the center of rotational symmetry.
| The answer is shown in the figure. |
Solved math task 2
What different types of symmetry are there in the image?
Answer:
| Line, rotational and identity symmetry. |
Solved math task 3
How many angles of rotational symmetry are there?
Answer:
| 4 – 90°, 180°, 270°, 360°. |
Symmetry: practice math problems
Symmetry worksheets
Brighterly offers math worksheets on symmetry to help your kid learn and practice:
Problems with Geometry?
- Does your child need extra support with understanding geometry?
- Start lessons with an online tutor.
Choose kid's grade
Is your child finding it hard to master geometry? An online tutor could be of help.
