Least Common Denominator
reviewed by Jo-ann Caballes
Updated on October 8, 2024
Welcome to another Brighterly guide on essential math concepts.
Learning math doesn’t have to be difficult or intimidating – we make math concepts cool to learn and easy to understand.
Today we’ll be covering the least common denominator (LCD). It’s an essential mathematical concept that relates to other core math elements, including fractions.
Here, we’ll cover the LCD meaning, how to find the least common denominator, the LCD of fractions and real-life applications. We’ll also share solved and practice math tests to allow you to put your knowledge to the test!
What is the least common denominator?
The least common denominator, also known as the lowest common denominator or LCD in math, refers to shared multiples in the denominators of fractions. It’s used in math to compare, add or subtract fractions with denominators that are different (aka unlike denominators).
By finding the least common denominator, you can make these calculations easier and more manageable. We cover the full definition of the least common denominator below.
Least common denominator: definition
The least common denominator LCD definition is the smallest possible multiple that two or more denominators of fractions share. In other words, it’s the smallest number that can be divided by all denominators.
For example, the least common denominator of the fractions ½, ¼ and ⅚ would be 12, because that’s the smallest number that can be divided by all three denominators.
The least common denominator can also be one of your original denominators. If we take ⅓ and ⅚, the lowest common denominator is 6, because it is the lowest number divisible by 3 and 6.
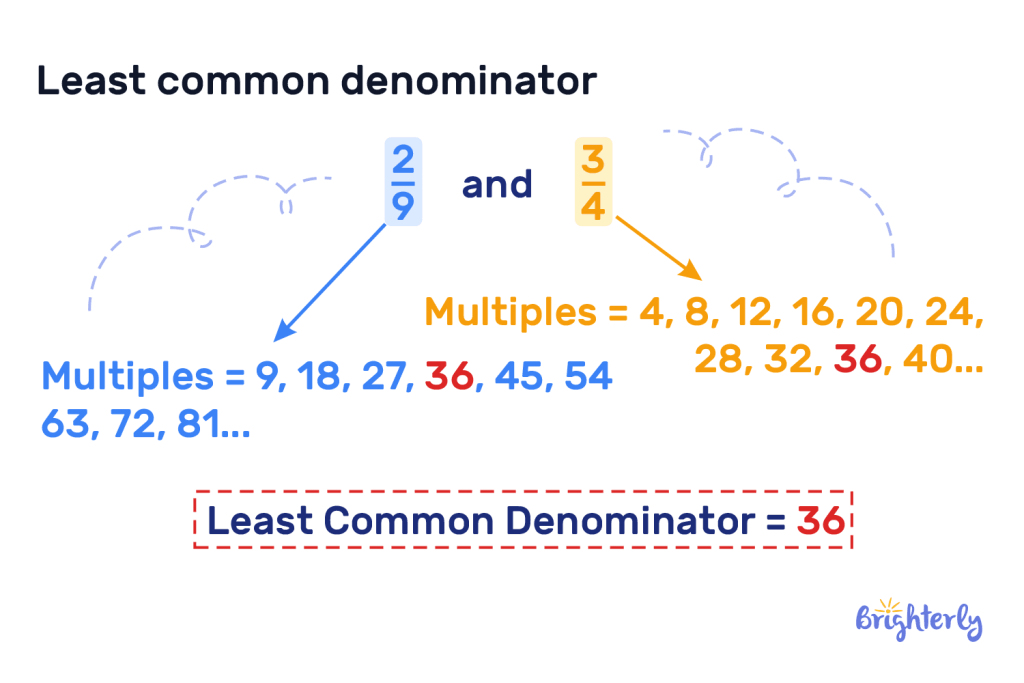
Because there can only be one smallest number both your denominators are divisible by, there can only ever be one lowest common denominator. You can have multiple common denominators, because there will be more than one multiple your denominators share. But you can only ever have one least common denominator. Your least common denominator can also never be 0, because you can’t divide 0 by any number and get a positive integer.
Ways to find least common denominator
There isn’t a lowest common denominator formula, but there is a simple way to find your least common denominator that makes it easy – and in turn, can make working with fractions with unlike denominators a breeze!
Take these simple steps to find your lowest common denominator of your unlike fractions.
- List the multiples of each denominator.
- Find the smallest multiple that all the denominators share. This is your least common denominator!
Let’s use a least common denominator example here. If you wanted to find the lowest common denominators of 1/12 and 3/7, first you would list the multiples of each denominator.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, …
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, …
You’ll see here that the lowest multiple both numbers have in common is 84, so this is your least common denominator.
Then, you’ll need to work out what multiple your least common denominator is of both your numbers. 12 x 7 = 84, and 7 x 12 = 84, so you’d need to multiply your first numerator by 7, and your second numerator by 12, giving you 7/84 and 36/84.
Applications of least common denominator
The least common denominator has a lot of real-world applications that make everyday activities easy to work out. They include:
- Sharing tasks, resources or items evenly amongst a group of people
- Comparing and converting measurements in carpentry, cooking and other activities
- Simplifying a range of complex math problems, making them easy peasy to solve
Comparing & ordering fractions
To order or compare a range of fractions from the smallest to the largest, you’ll need to use the least common denominator. First, find the lowest common denominator of all your fractions’ denominators. Then, what you’ll need to do is convert each fraction to an equivalent fraction using your least common denominator.
Once you’ve found your lowest common denominator, you need to know what you multiplied each denominator by. For example, if we use ⅗ and 3/7, our multiples are:
- 5: 5, 10, 15, 20, 25, 30, 35, …
- 7: 7, 14, 21, 28, 35, …
35 is the 7th multiple of 5, and the 5th multiple of 7, so this is what you’d need to multiply your numerators by:
- 3 x 7 = 21
- 3 x 5 = 15
Your final fractions are 21/35 and 15/35, then you’ll arrange them with your smallest numerator first, so your final order will be 15/35 and 21/35.
Using the least common denominator here, we can compare the fractions on a common scale, making it much easier to work out their relative sizes.
Adding & subtracting fractions
Adding and subtracting fractions with unlike denominators is super easy if you use the least common denominator method. When you work out the least common denominator and convert all your fractions to ensure they have like denominators, you can easily add and subtract numerators from one another without any additional conversions!
Let’s use a least common denominator example and add ⅖ and ¾. Our multiples are:
- 5: 5, 10, 15, 20, …
- 4: 4, 8, 12, 16, 20, …
We can see that our lowest common denominator is 20, so our converted fractions are 8/20 and 15/20. Added up, they total 23/20.
You don’t need to use the least common denominator when multiplying or dividing individual fractions, because you don’t need to find any common ground in them – you can simply multiply or divide them by your integer. You can’t multiply or divide fractions by one another because they are not positive integers.
Solved math tasks: examples
Ready to put your new-found knowledge on the least common denominator in fractions to the test? We have put together some math task examples, along with their solutions, so you can practice your knowledge. Take on our challenges and then check your answer at the end to see if you got it right!
Solved math task 1
Find the lowest common denominator of 2/4 and 4/6.
Answer:
| The lowest common denominator is 12, and your final fractions are 6/12 and 8/12. |
Work out the multiples of 4: 4, 8, 12, 16, …
Work out the multiples of 6: 6, 12, 18, 24, …
The smallest common multiple is 12, so the lowest common denominator is 12.
Solved math task 2
Order the fractions 2/3, 1/2, and 3/4 from least to greatest.
Answer:
| ½ (6/12), ⅔ (8/12) and ¾ (9/12). |
First, find the least common denominator of the denominators: 3, 2, and 4.
Least common denominator = 12
Convert the fractions to equivalent fractions with the least common denominator as the denominator:
2/3 = 8/12, 1/2 = 6/12, and 3/4 = 9/12
Order the fractions based on the size of the numerator: 1/2 (6/12), 2/3 (8/12), and 3/4 (9/12).
Least common denominator: practice math problems
Least common denominator: worksheets
The least common denominator is like a secret weapon for simplifying a range of math problems and operations. See how much quicker you can work through a range of sums and problems with our free math worksheets:
- Common denominator worksheets
- Rationalizing the denominator worksheets
- Fractions worksheets
- Adding fractions with like denominators worksheets
Problems with Equations?
- Is your child finding it hard to grasp equations fundamentals?
- An online tutor could be of assistance.
Choose kid's grade
Does your child struggle with mastering the basics of equations? Try lessons with an online tutor.
