• Math tutors
• /
• Blog
• /
• How to Teach Kids Division?

How to Teach Kids Division?

There are many approaches to teaching division to kids. Some of them need just you and the child, while others require expert help, whether from the school teacher or a third-party tutor. For instance, the innovative education platform Brighterly offers a wide range of activities for learning math, including fun ways to teach division.

Today, we want to share with you 10 ways to teach division as a parent to a child. These methods are not only great ways to learn math, but they also can strengthen family bonds.

How to teach division with Brighterly?

The key to teaching division is the holistic approach, as this experience involves all significant adults in kids’ lives, from parents and relatives to tutors and teachers. This approach allows the child to safely learn division without any knowledge gaps that can ruin their math skills in the future.

That’s why the Brighterly math tutoring platform offers you tutor sessions, articles with helpful info, and free worksheets to test a kid’s math abilities. We conduct all our tutoring sessions online, so your child can learn math wherever they want to.

Later, solidify the results from Brighterly Math tutors using free worksheets and examining the child using our articles and Common Math quick tests.

Here is an example of an interactive math problem in our division-themed article where your child can test their knowledge.

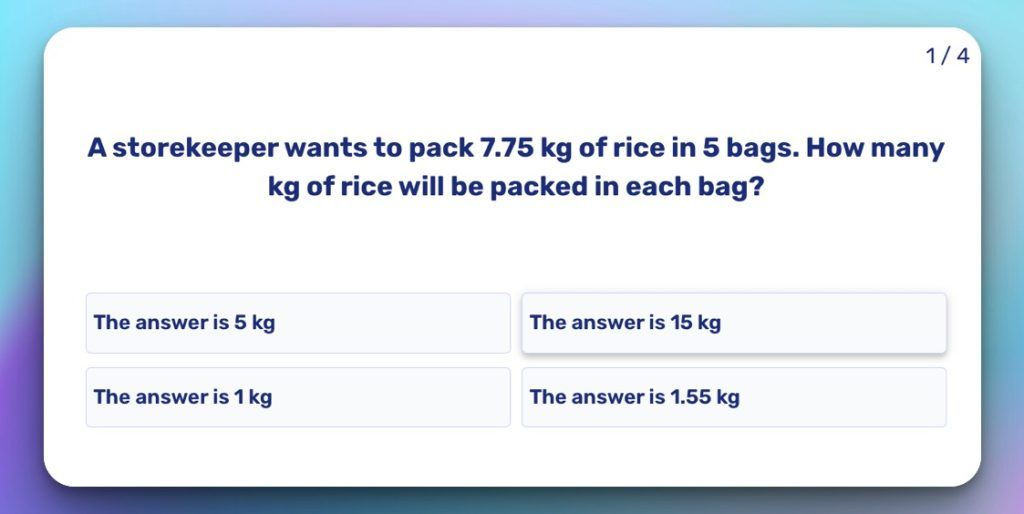
When do kids begin to learn division?

In most cases, a full-fledged study of this topic starts from 3rd grade; however, kids begin to learn division starting from kindergarten. The best way to teach division to younger kids is to show real-life examples.

You don’t need to write complex equations. Start with easy tasks such as “Dolly and Vanessa have 24 apples together. How many apples does each of the girls have if they have an equal amount of fruits?”. Those easy problems show them that a knowledge of division is vital for daily life.

This is an example of easy division for grade 2, and those easy problems will be more than just enough for the youngest kids. All you need to do is to experiment with numbers while leaving the basic math problem as simple as possible. You need to ensure that the child understands the basics.

How to teach simple division to 1st and 2nd-grade students?

While you teach division to 1st and 2nd-grade students, keep it simple and tangible. These kids are just learning basic concepts, and division problems could be too complex for them.

Grab manipulatives and show them that math isn’t just some numbers but real objects that are easy to manipulate. If you are on the road and can’t use real-life objectives, download worksheets that show how to teach division to grade 2. All you need to do is print those papers, give your child a pen, and be near them to help when needed.  

How to explain division to a child? [from 3rd grade]

To explain division to a child, try special techniques to help understand the strategy of patterns. Speaking of how to teach division to grade 3, it’s worth showing them that any multiplication is just a series of additions, and division is the inverse operation of multiplication.

For instance, the math problem can ask your child to divide 32 balloons between 8 kids. But if your child doesn’t remember the multiplication chart, it can be complex.

Understanding division logic makes it easier even without chart memorization. As the first step, you can perform an easy 8 + 8 operation to determine that 8 x 2 is 16. The next step will be to add 16 + 16, which is basically 8 x 4. Your child will get the 32 as the answer. It means that 32 ÷ 8 = 4. So, each kid will get 4 balloons.

If you are interested in how to teach division to grade 4, you just need to do the same: ensuring that your child remembers the multiplication chart and understands the interconnection of math operations. The overall process of learning division for kids stays the same, just with more complex problems involving square roots, fractions, and decimals.

8 ways to teach division

• Understanding division as sharing
• Division vocabulary
• Relating division to multiplication
• Division without remainders
• Division with remainders
• Dividing decimals
• World problems and applications
• Checking work using multiplication

Best way to teach division #1: Understanding division as sharing

The easiest way to explain division to a child is to show how to split things evenly. This ability is core and influences the way learners understand the purpose of division. When the child can count and group things well, you can start splitting exercises. As a rule, it becomes possible in the second or third grade. 

To make a division for beginners simple, show how to do it in everyday life. Take 10 apples and tell them to share them equally between 2 people in the room. Later, you can make it harder and ask for sharing fewer items between a bigger number of people.

Best way to teach division #2: Division vocabulary

Talking correctly about the process with a proper division vocabulary and real-life examples is an important part of learning. How to teach division for beginners? Start talking about it step by step, and the child’s interest will rise. The important division words are dividend, divisor, quotient, and remainder. 

For instance, in the case of 10 apples, you can teach a child to talk in the following way:

You can describe each sharing situation in such a way. A clear understanding of naming parts of patterns will help learners orient better.

Best way to teach division #3: Relating division to multiplication

Make math relatable to daily situations while teaching them division. When explaining this action to a child, you should relate it to concepts that the kid already knows. As soon as the child understands the sharing mechanism in everyday life, turn to the multiplication connections. Once they understand the connection between multiplication and division and their reversibility, it becomes times easier to solve any equation.

Children are ready to understand it when they are aware of sharing principles and division vocabulary. Start teaching with simple questions. From the multiplication table, the student knows that 4 × 5 = 20. You can say:

The main idea is to catch the relationship between divisions and multiplication tables. 

Best way to teach division #4: Division without remainders

When the child understands vocabulary and the core meaning of divisions, it is time to say that it can end without whole numbers. Each simple division ends with the number, but there can be a remainder.

To make the learning division process more understandable, take 12 cookies and ask to divide them between 3 people. You can draw the scheme on the paper to make it clear. Subtract one cookie each time till you reach zero. 

Different worksheets are an effective way how to learn division for beginners. It gives your child more practice and explains information to children with pictures and graphics. We, at Brighterly, offer you division worksheets to sharpen the kid’s knowledge. Just download them and start improvised home study sessions. 

Best way to teach division #5: Division with remainders

Division with remainder can become more complicated to understand, so you need to ensure that the child understands the logic of the “without remainder” concept. Use simple division teaching methods to explain division, which consists of dividing fruits or cookies at home.

Dividing 10 apples between 3 people, you will face a problem when one apple is left. To divide it, cut the remaining apple into 3 equal parts. When kids understand the concept of division with remainders in everyday life, tasks on the paper will be more apprehensible. 

Best way to teach division #6: Dividing decimals

This approach involves dividing numbers that have decimal points, starting with dividing decimals by whole numbers before moving on to dividing by decimal points themselves.

This division level is more serious and demands a good knowledge of previous concepts. Starting teaching divisions, persuade your child to understand decimals’ meaning and place value. 

Start by dividing the decimal point by the whole number, using the same long division process, but paying attention to where the decimal point is in the fraction. Use real-life examples about money or measurements so the kid can relate a problem to a real-life situation. Then, enter the division by the decimal fraction, showing how to move the decimal point to make the divisor a whole number.

Best way to teach division #7: World problems and applications

Once your child is comfortable with easy number-based daily examples, it’s time to explain division for kids with words and how to apply it to complex matters. You should transfer the child’s attention to global worldwide issues.

When the student understands the meaning of division in tackling world problems, the attitude to learning and assignments will change. An easy way to learn division meaning in the global sphere is by reading different articles and discussing how division works in each situation. It is important to provide a lot of practice in dividing into groups or dealing with measurements.

Best way to teach division #8: Checking work using multiplication

Division and multiplication are inverse operations, so one of the best ways to teach division is to allow students to check their work using multiplication. To learn division in that way, ask the child to multiply the quotient by the divisor.

When the result is the dividend, the task is done correctly. Division for kids brings more attention to the actual principles behind it, improving multiplication knowledge.

4 easy ways to teach division: effective methods for kids

• Visualization is the best way to teach division
• Column division for beginners
• Playing games like Monopoly
• Cooking is fun 

Easiest way to teach division #1: Visualization is the best way to teach division

Visualization is an easy way to learn division for any kid or adult. Math is a pretty intangible subject, especially when it comes to complex subjects. Luckily for you, the division is a basic math operation, so you can easily visualize it with charts, graphs, and daily objects.

Easiest way to teach division #2: Column division for beginners

Column division (a.k.a. long division) is one of the easiest ways to teach division and strengthen the number sense. During this process, the child uses all other math operations, which helps them boost their addition, subtraction, and multiplication skills.

Use the “Dad, Mom, Sister, Brother” Mnemonic as an easy way to explain division. This can help children remember the order of the steps: Divide, Multiply, Subtract, and Bring Down.”

The column can be divided in different ways. 

• Write the number to be divided (dividend). On the right, write the number to be divided by (divisor). 
• Separate the dividend and the divisor with a dash, and underline the divisor with a horizontal dash. A corner should be formed. 
• Next, determine the first incomplete divisor – the smallest number that can be divided by the divisor. At first, when the child learns to divide in a column, it is advisable to circle each incomplete division with a parenthesis from above. Circle the first incomplete divisor with a parenthesis and the rest of the following numbers as well. 
• Calculate how many digits the fraction will consist of (the result of the example). You can put dots in place of the numbers that will form the number of the fraction. There are as many brackets above the divisor as there are dots under the divisor. 
• Calculate how many times the divisor will fit in the first incomplete divisor. To do this, divide the first incomplete dividend by the divisor. Write down the result without a remainder in place of the first dot. 
• Multiply the number you wrote down in the result by the divisor. Write the product under the first incomplete divisor. 
• Subtract this result from the first incomplete divisor to find the remainder while teaching kids division.
• Write the number of the next digit of the division next to the number of the difference obtained in the previous step. If zero was obtained, then it is not necessary to write it down. 
• Divide the received number by the divisor. Write the result in place of the second period.
• Multiply the number written as the second in the result by the divisor. Write the product under the second incomplete divisor.
• Subtract both numbers. If the result is zero, it means that the equation is solved.

Easiest way to teach division #3: Playing games like Monopoly

If you are looking for an easy way of teaching division to grade 2, try playing games like Monopoly. Start with simple scenarios where players must share their money equally among a certain number of people (e.g., dividing $100 equally among 4 players). After that, introduce uneven division to teach child operations like “divide the $250 among the 4 players”.

Discuss how players can budget their money by dividing it into different categories. If you wonder how to learn division for beginners without any pressure – this is one of the best ways.

Easiest way to teach division #4: Cooking is fun

Cooking is a fantastic approach to teaching children division in a fun and practical way. You can teach them to divide ingredients for correct recipes, measure components, and convert them to preferred systems. You can bake some European pastry and ask the child to convert milliliters to ounces.

The top 3 difficulties of teaching division

• Difficulty in visualizing division
• Misunderstanding the inverse relationship between multiplication and division
• Forgetting steps in long division

Difficulty in visualizing division

Difficulty in visualizing division is one of the most common student problems that prevent them from academic success. When learning how to divide, convert abstract tasks to concrete objects and real-life situations. Use visual aids like diagrams, number lines, and area models to represent division visually. These tools can make the abstract process more concrete.

Sometimes, it is hard for parents to draw such patterns or find ideas on how to make them.  In this case, you have to turn to an innovative educational platform that can provide your child with specialized programs and methods aimed at explaining and making things clear.

Brighterly Math platform works with children of different ages and gives great and complex knowledge to kids. Click the Register Now button and provide your child with the opportunity to learn math faster with professional tutors.

Misunderstanding the inverse relationship between multiplication and division

Another common mistake is missing the actual relationships between multiplication and division. Before switching to division, you need to ensure that a kid has no knowledge gaps in multiplication. 

Ensure that children have a strong foundation in multiplication facts. Introduce fact families to show the relationship between multiplication and division. Only after the kids are strong in multiplication can they be taught to divide.

Forgetting steps in long division

The third common mistake in learning how to divide is to forget steps in the long division. To help with remembering, try to remind them about these steps while teaching.

Break down the long division process into smaller, manageable steps. Use mnemonics to “Divide, Multiply, Subtract, Bring Down”  like “Does McDonald’s Sell Cheeseburgers?” or “Daddy, Mommy, Sister, Brother” to help children remember the correct order.

You can create an interactive algorithm of steps, adding curious pictures and schemes. It will attract the child’s attention and will boost remembering. After several reminders, it will become easier to reflect on steps in long division.

Top ways to teach division: conclusion

As you can see, there are many ways how to explain division to the kid, and each has its specifics. But they all have one thing in common — they are all about making math palpable and understandable to the kid.

Math worksheets from the Brighterly team can help your child better understand even the most complex aspects of this subject. The easiest way to teach division to elementary and middle school kids is to combine tutoring and additional practice with the parents. When professional tutors help the students seal their knowledge gaps, parents help the kid solidify their knowledge.

Book a free demo lesson with Brighterly today to see how a holistic approach to math can benefit your child!