• Math tutors
• /
• Knowledge Base
• /
• Line Segment – Definition, Formula, Examples

Line Segment – Definition, Formula, Examples

Jessica Kaminski

reviewed by Jo-ann Caballes

Updated on October 8, 2024

At Brighterly, we’re committed to making math easy to understand and fun to learn.

Here, we’re going to cover everything you need to know about line segments, a core element of geometry.

We’ll answer the question: “What does a line segment mean?” and share their formula, examples and practice math problems.

What is a line segment?

A line segment is a geometric concept that forms the basis of many shapes, including triangles, rectangles, polygons and polyhedra. They help us understand the relationships between shapes and solve problems with math concepts including angles, areas and lengths. We’ve included the geometry line segment definition below.

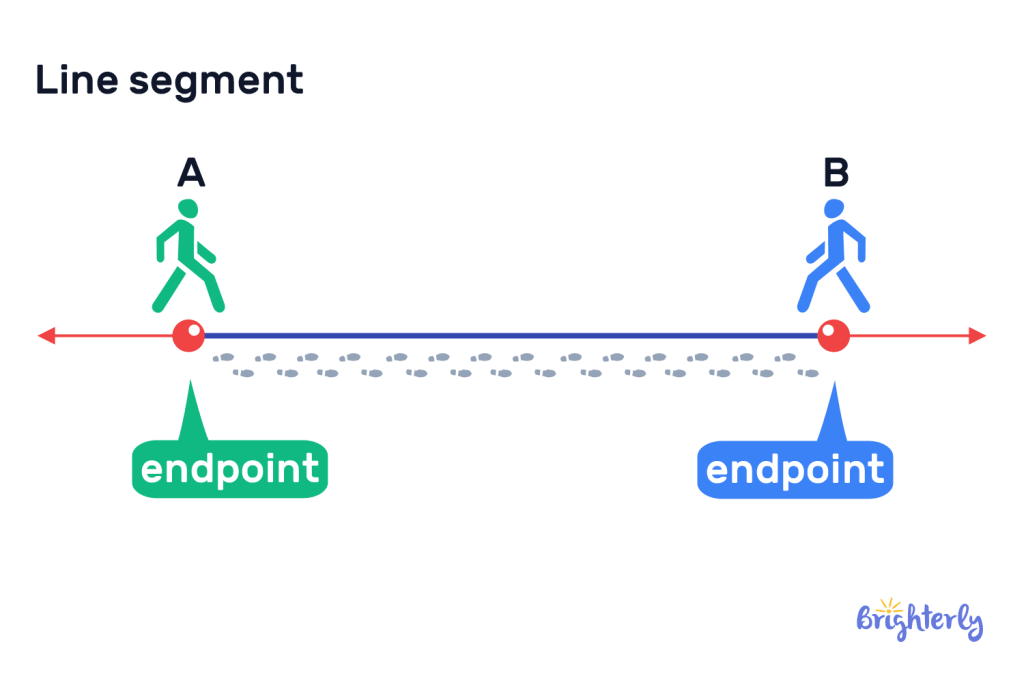
Line segment definition

The line segment definition in geometry is the portion of a line with two specified endpoints, meaning it has a definite length. Draw a line and mark two points on it – the portion of the line between the two points is the line segment.

Math tutors

Join Brighterly for personalized lessons for your child

Meet the best tutors for interactive math learning.

Book free lesson

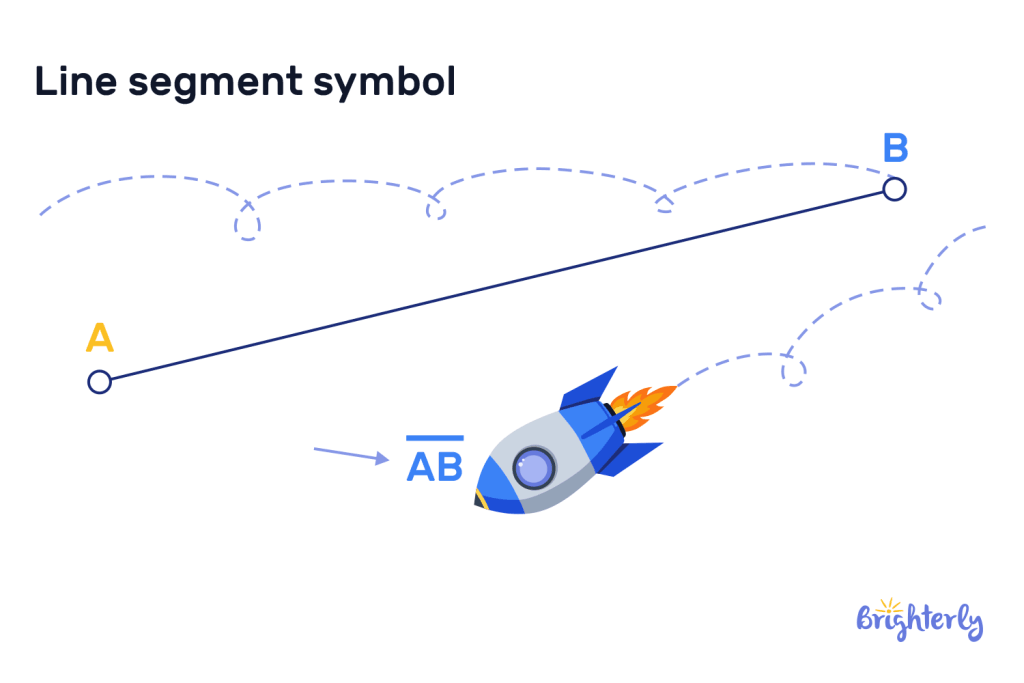
Line segment symbol

Line segments can be represented by symbols. One symbol comprises two uppercase letters that label the endpoints, e.g. AB. Line segments can also be represented with the “overline” notation, e.g. A̅B̅.

Real-life examples of a line segment

There are many real-life examples of line segments as they’re represented in many structures, objects and natural formations. Here are some real-life line segment examples:

1. Square or rectangle-shaped book’s edges.
2. The edges of sports courts and fields, e.g. basketball courts, tennis courts or soccer fields.
3. The length of objects such as toothbrushes, pens or pencils.
4. The journey between two specified points on a GPS device or map.
5. Building design features, such as wall outlines, doors or windows.
6. A spider’s web, where the joints are line segments.

How to measure a line segment?

Measuring a line segment is straightforward. First, understand the scale of the object and the unit of length, whether that’s centimeters, meters or inches. 

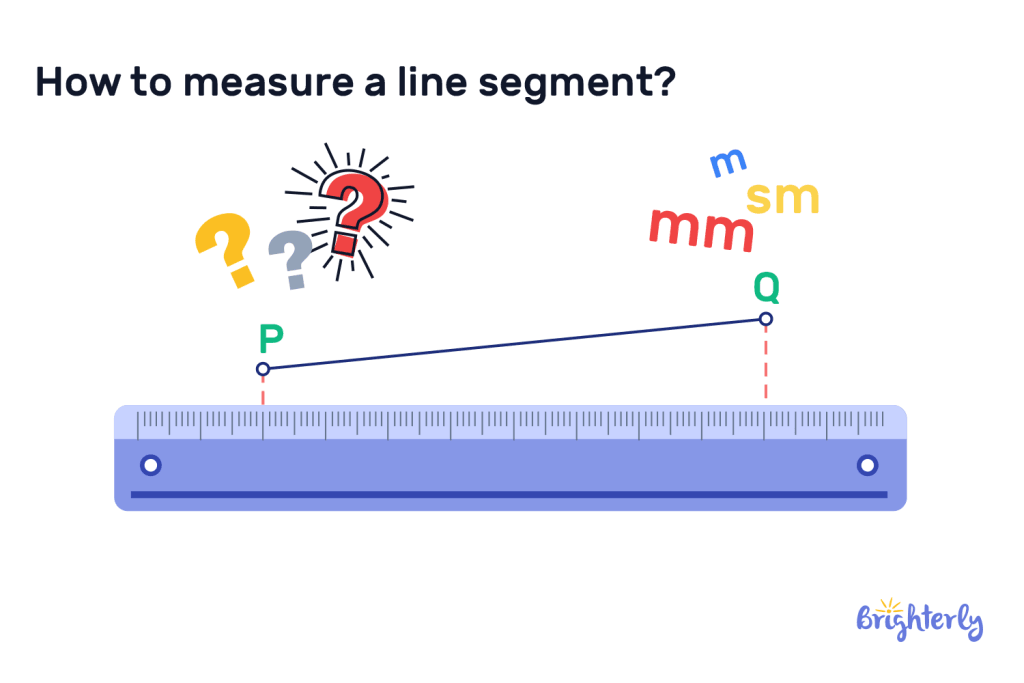
Steps to measure the length of a line segment:

1. Place the beginning of your ruler or measuring tape (the zero mark) at the starting point (known as endpoint A).
2. Keep the ruler or measuring tape parallel to the line segment, stretching along if required.
3. Mark where the ending point (known as endpoint B) is on your ruler or measuring tape.
4. That number is the length of the line segment.

How to find the length of a line segment

You can find the length of a line segment by measuring it. Use the instructions we’ve detailed above to find the length of your line segment.

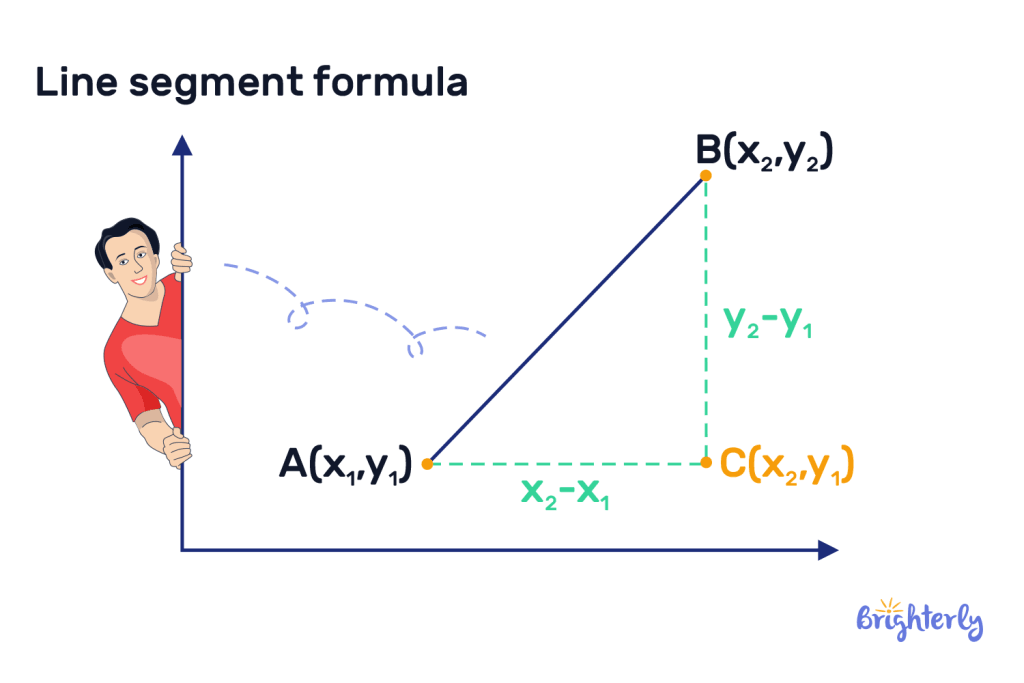
Line segment formula

Individually, line segments don’t have formulae. But when on a coordinate plane, you can find the length with the following formula:

Distance = √((x2 – x1)² + (y2 – y1)²)

Endpoints A and B are represented by (x1, y1) and (x2, y2) respectively.

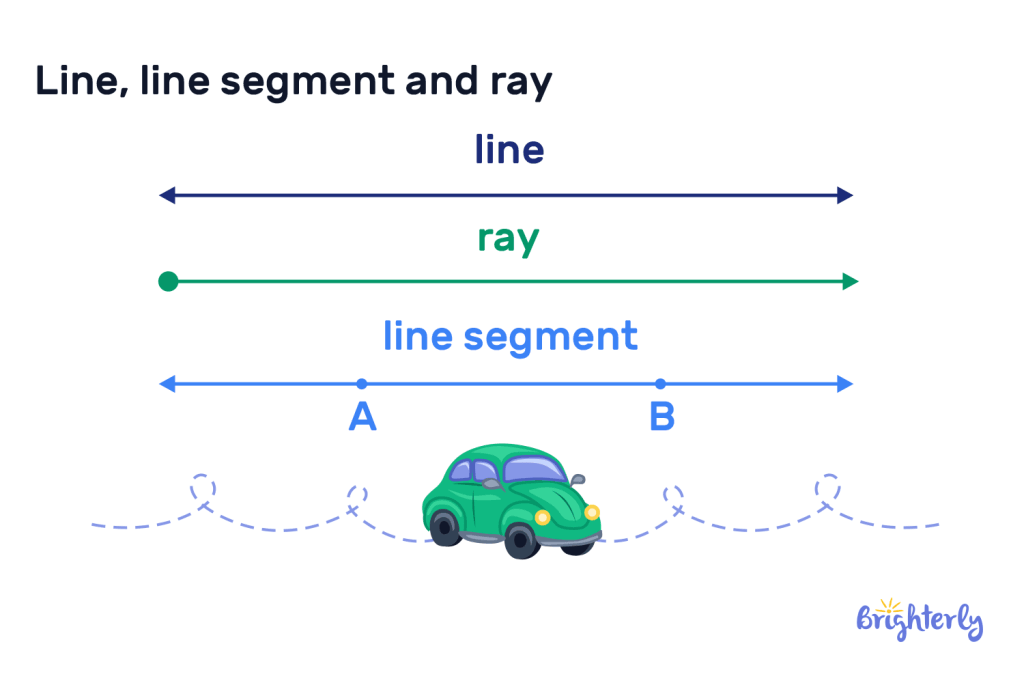
Difference between line, line segment and ray

A line has no endpoints, extending infinitely in both directions. A line segment has two defined endpoints and therefore a defined length. A ray has one endpoint, and the other end extends infinitely, meaning it’s a combination of a line and a line segment.

Solved math tasks: examples

Line segment practice math task 1

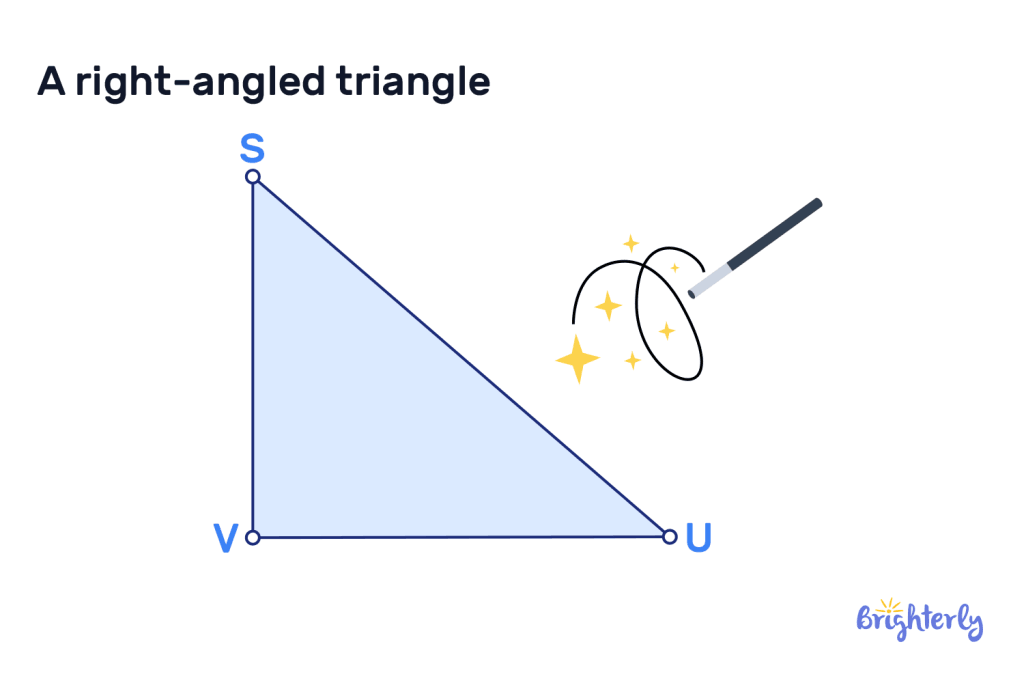
Using graph paper, draw two perpendicular line segments, each covering four units, extending from point V. now, connect the two line segments. What shape have you created?

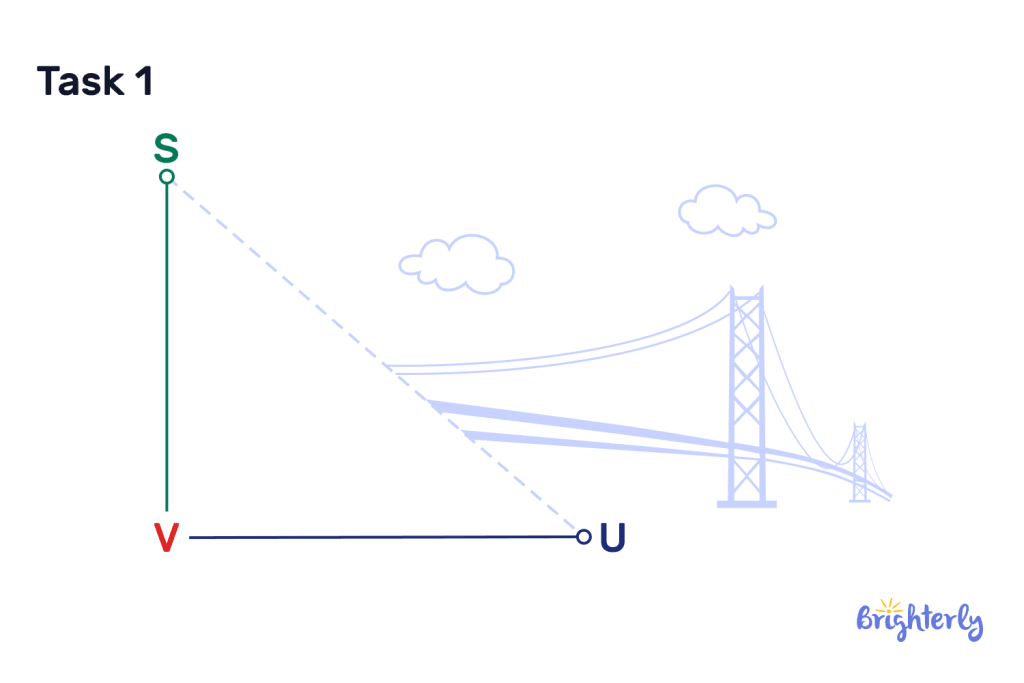
Answer:

Line segment practice math task 2

What’s the difference between a line and a line segment?

Answer:

Line segment practice math task 3

Draw all of the available line segments between the points of D, E, F and G.

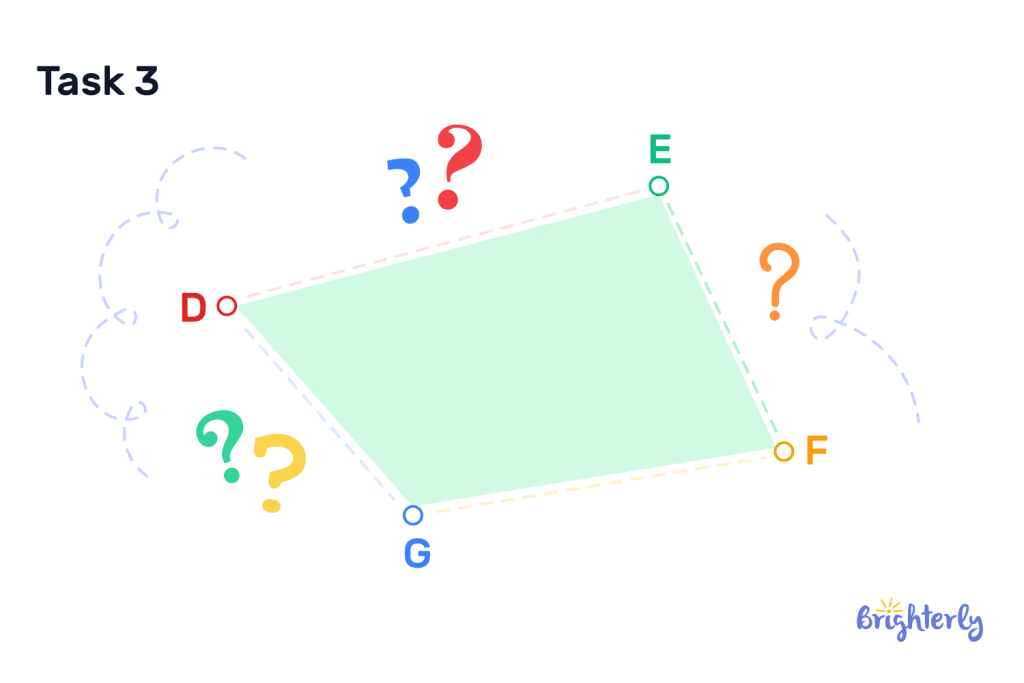
Answer:

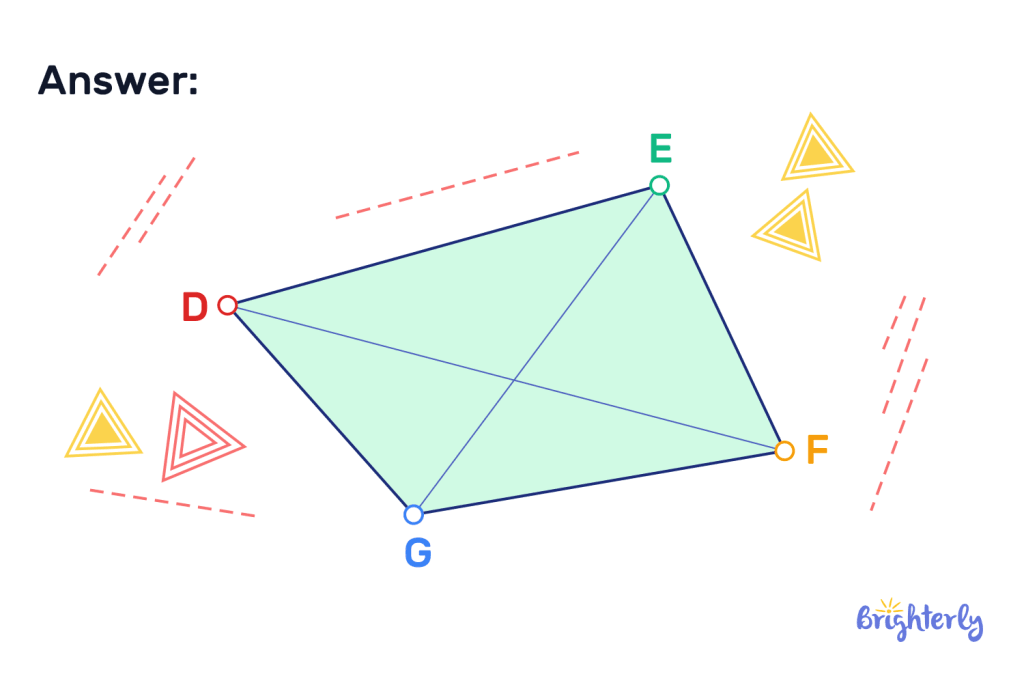
Line segment: practice math problems

Line segment worksheets

Brighterly offers math worksheets to help your kids learn and practice line segments:

• Ruler measurement worksheets
• Measurement worksheets
• Lines and angles worksheets
• Parallel and perpendicular worksheets

Jessica Kaminski

72 articles

Jessica is a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.