What is Zero: Definition, Examples, and Practice Math Problems
reviewed by Jo-ann Caballes
Updated on November 12, 2024
One of every child’s first math-related questions is “What is 0?” or “Is 0 a real number?”.
In this article, we explain the concept of zero through the definition of zero, give zero examples, and explore the importance of zero in math
What is 0 in math?
Zero in math doesn’t just mean nothing. It is a number with its own unique properties which is essential in math, algebra, and arithmetics.
Zero has had a long history in math and its origin dates back to many early societies such as the Maya civilization (4th century CE) where zero was used in their calendars for tracking days.
Ancient Egyptians recognized the absence of something and had symbols to denote this, however, they did not take 0 as a number.
Zero was also used in ancient India and Arab civilizations where the concept of zero as a number was developed along with its properties before this number reached Europe and is now leveraged for everything in math, arithmetics, and even computer science.
Why is zero important in math?
The importance of zero in math cannot be overstated because of its distinct characteristics and uses.
0 is the number used to express the nonexistence of a positive or negative number.
The number zero is the only number that doesn’t affect any number when added or subtracted. Zero is expressed as “0” in figures and is one of the integers.
Remember that integers are whole numbers without fractional remainders or decimal components, these are positive numbers, negative numbers, and our subject topic, zero.
Also, with zero, we can have placeholders for numbers with no digits for the place values. We discuss this more below.
Properties of zero
There are various properties that make number 0 unique. Zero is a non-positive and non-negative integer which is why it has its own set of properties.
These properties explain how zero relates to other numbers using arithmetic operations: addition, subtraction, multiplication, and division.
Let’s take a closer look at them:
Addition property
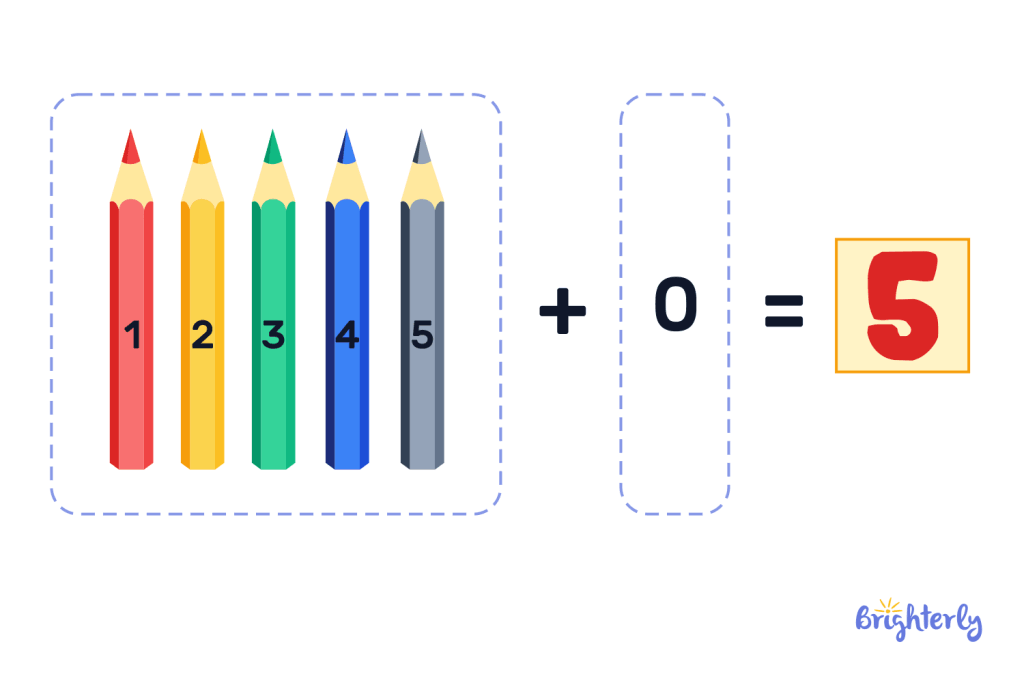
The addition property of zero is the rule that mandates that if we add the number 0 to any number, the number remains unchanged.
Look at it this way: if you had a box of 5 pencils, and you added exactly 0 pencils to it, you would still be left with 5 pencils which means nothing has changed.
Subtraction property
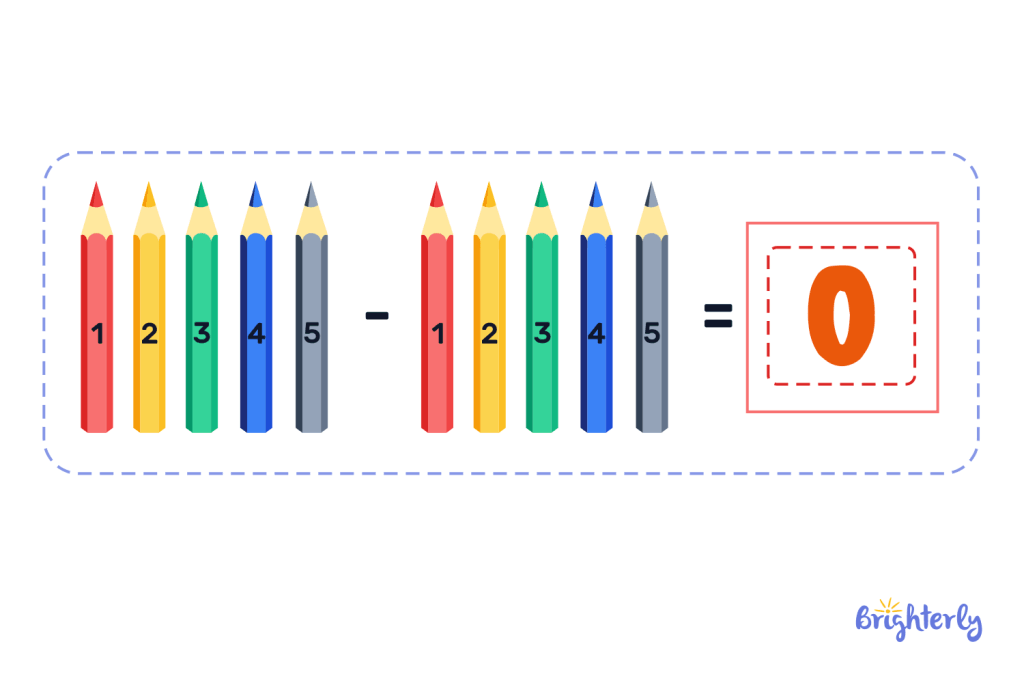
This property says that when we subtract the number 0 from any number, the number remains the same. Once again, if you had a box of 5 pencils and you removed 0 pencils from it, you would still be left with 5 pencils.
The subtraction property also says that if we subtract a number by itself, the result would be 0. When you remove 5 pencils from your box with only 5 pencils, none will be left, meaning 0 pencils will remain.
Multiplication property
This property tells us what we already know — when any number is multiplied by number 0, the result will always be 0.
When broken down, multiplication is simply addition but without the extra steps. For example, when we multiply 2 by 5, this is 2 + 2+ 2 + 2 + 2 = 10. This means we have added 2, five times.
However, when we are to multiply by 0 (take 5 x 0 for instance), we cannot possibly add 5, zero times. Therefore, any number multiplied by 0 simply results in 0.
Division property
Division by the number 0 is impossible — plain and simple. Mathematical scholars term it as “undefined”. This means 5/0 will result as undefined since there is no logical explanation for it.
However, this property also states that when we divide 0 by a number the answer is 0. For instance, 0/5 = 0.
What does a zero with a line through it mean in math?
A zero with a line through it, or a slashed zero (∅) means an empty set in math.
To explain, let’s assume we had two sets (X and Y):
X= {2, 4, 6, 8, 10}
Y= { }
The X set has values within it but the Y set is empty which means Y = ∅.
Please note that ∅ and number 0 are not interchangeable and are different concepts in math. 0 is a unique integer with properties and ∅ is used to represent an empty set.
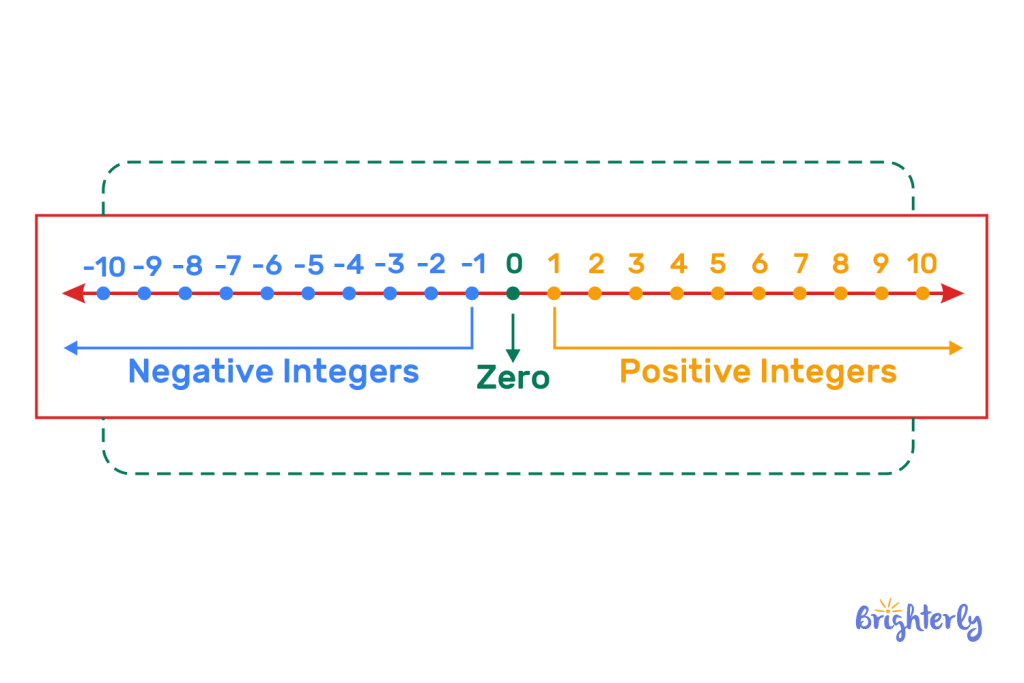
Zero number on the number line
On the number line, number zero is located between -1 and 1. Remember that it is neither a positive nor negative number, so its position on the number line reflects that.
Zero as a placeholder
Zero as a placeholder is used to show the correct value of a figure even if there is no digit in the place value it takes.
For instance, in the number 305, 0 holds the tenth place and we can tell that the number is in the hundred because of 0.
Without the placeholder zero, we would take 305 for 35 and may confuse it for 35. What about numbers such as 30005?
Zero as a decimal placeholder
The placeholder zero doesn’t just work for whole numbers, it also applies to decimals as well.
For the decimal number, 4.05, zero is a placeholder of tenths. In 4.606, it is the hundredths, and so on.
However, unlike whole numbers where zero can be a placeholder if it is in the rightmost part of the number such as in 3750, it is not the same for decimals.
When a decimal number ends with zero, such as 3.420, we can approximate it to 3.42 and just ignore the 0 because in this case, it has no value.
Solved Math Tasks: Examples
Solved math problem 1
Solve this equation: 52 — 11 — 40 + 0 —1
Answer
| 52 minus 11 is 41, and 41 minus 40 is 1. |
Remember that one of the properties of zero is that when added to a number, the number remains the same, therefore, 1 plus 0 is 1, and 1 — 1 is 0.
Solved math problem 2
Which of the following statements are true, and which of them are false:
- When we divide zero by a number, the result is 0
- When we multiply 0 by 0, the result is 1
- Zero is not a number
- Zero is between the positive and negative numbers on a number line
- In the number 3805, number 0 is useless
Answer
|
Solved math problem 3
Solve this equation: 17808332 × 50009 × 1999087 × 0
Answer
| The answer is 0. |
Number 0: Practice Math Problems
Number 0: worksheets
Zero is a very important number. The number plays a significant function in mathematics, you can find zero in geometry, math, algebra, and so on.
Therefore, your child’s understanding of this special number is necessary. Luckily, Brighterly also offers free worksheets on zero:
Need help with Numbers?
- Is your child having trouble understanding numbers fundamentals?
- An online tutor could provide the necessary support.
Choose kid's grade
Does your child need extra help with mastering numbers lessons? Start studying with an online tutor.
Book a Free Class
